Крючков Фундаменталс оф Нуцлеар Материалс Пхысицал Протецтион 2011

·the input to estimate the quantity Y is the values уi obtained by measurements, as well as random errors S(yi) and the systematic error θ (Y) calculated in one of the experiments;

·the result of determining the quantity Y shall be estimated as follows:

Calculation of ID errors

A system to account for NM as any other material and articles of value is based on balance closing, the major tasks in which are inventory taking, handling and statistical analysis of the data obtained (determination of the statistical significance). The basic assumptions one needs to analyze the ID significance are as follows:

·it can be assumed fairly credibly that the ID obeys to normal distribution law with a zero mathematical expectation and the variance of

σID2 ;

·the confidence interval is to be selected subject to regulations and

requirements [4]. Therefore, estimating the ID value and the variance σ ID2 is enough to conclude on potential anomalies.

Since this is essential, let us discuss in more details the procedures and methodology to estimate the ID statistical significance for detecting anomalies during the material balance closing for an MBA.

The ID is determined and its statistical significance is estimated based on the physical inventory taking data so, as to anomalies, in the given case

191

we will deal only with an anomaly showing itself in the ID modulus exceeding the threshold values set in the General Rules [4].

To calculate the ID variance, the equation is expressed as the function

of:

∙ the input quantities – direct and indirect measurem ents (calculation or another determination) data for nuclear material parameters (concentrations, volumes, contents, weights, masses and so on) x1,..., xn ;

∙the random deviations of the given parameters r1,..., rn as conditioned by the random errors of parameter measurements;

∙the systematic deviations of the parameters s1,..., sn as conditioned by

the residual components of the systematic errors of parameter measurements:

ID = f (x1,..., xn ; r1 ,..., rn ; s1,..., sn ) .

The ID variance will be found by the following expression:

The ID variance or the total root-mean-square error is obtained by expanding the ID function into a Taylor series about the mathematical expectations of input quantities with the terms of the given expansion being limited only to linear terms. Individual derivatives are taken at the point x1 ,..., xn while no allowance is made for the deviations and variances of

parameter measurements for the NM inventory as of the inventory taking time in the products not changed since the preceding inventory taking and not measured for the accounting purposes in the given material balance period. Estimation of the ID statistical significance consists in finding out if the following two conditions are fulfilled [4]:

∙the ID modulus does not exceed the threefold root-mean-square ID error value;

∙the ID value does not exceed the found threshold quantities (G) with the confidential probability of 0.95.

The ID modulus exceeding the threefold ID root-mean-square error:

192

ID 3σ ID ,

testifies that there are anomalies present in the accounting and control system. The failure to fulfill the second condition:

ID G + 2σ ID ,

evidences of an anomaly present in the accounting and control system, this manifesting itself in the threshold quantities of nuclear material being exceeded.

4.4. Tests of hypotheses and sampling studies

A measurement process occasionally requires decisions to be made on the significance of the measurement data obtained, say, to find out if data from several series of measurements are consistent, if measurement data from several laboratories agree, or if the ID value has significance.

The final decision with respect to the significance can be made following a hypothesis test. For example, if the ID is significantly above

zero in a given period at a given facility.

Let Н0 be a zero hypothesis that consists in that ID≤0; and Н1 is an alternative hypothesis consisting in that ID>0.

As such, testing a hypothesis about a set of experimental data statistically fails to give any proofs as to whether this hypothesis is true or false. A detailed test simply indicates to what degree the hypothesis agrees with the experiment result.

A hypothesis test consists in calculating a certain criterion and comparing the value of this to the tabulated one. Therefore, a test of the zero hypothesis Н0 may suggest the following cases:

1)the hypothesis Н0 is just and the criterion permits Н0;

2)the hypothesis Н0 is just but the criterion discards Н0;

3)the hypothesis Н1 is just and the criterion discards Н0;

4)the hypothesis Н1 is just but the criterion permits Н0.

It is only in cases 1 and 3 that the hypothesis test leads to a correct result. The probability of a type I error (case 2) is numerically equal to the significance level α set for the hypothesis test. If the probability of a type II error (case 4) is equal to β, then the quantity 1– β is called the strength of the test. One often succeeds in giving a test more strength just by increasing α. In other words, a compromise is possible between the level of

193

significance and the test strength, a high strength occasionally turning out to be greater than small α.

Several basic hypothesis types are normally tested.

1.Is the measurement data described by the given distribution?

2.Is the difference between two average values significant?

3.Do the variances of several measurement series differ significantly?

Criterion χ 2

It happens sometimes that for the preset random sample хi (i = 1, 2,…, n) of the random quantity Х one needs to test the hypothesis that the function f(x) is the probability density for Х. To get the measure of the available data deviation from the anticipated data as per a hypothetical distribution, the quantity χ 2 is used. The criterion for testing the hypothesis is the comparison of χ 2 against the tabulated value χ 2р, which meets the preset р–percent significance level.

First, the whole range of the values Х in the given sample is broken down into m nonoverlapping intervals; m is found by one of the following formulas:

m = log2 n +1; m = 5 lg n;

m = 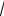n;

m = 1.9 n0.4 ,

or from Table 4.3.

Table 4.3

Recommended number of breakdown intervals depending on the number of events

Interval length: d = 1.02 X max

m

The boundaries of the intervals are determined as follows:

194

X min − D; X min + d − D;

............................................................

where D = 0.01d.

The number of the values falling into the i interval is equal to νi. If νi <5, the intervals merge. Let pi be the hypothetical probability that Х takes a value that falls into the i interval. Then

i =1

If the assumed number of values in each interval is more than 10 (i.e. npi

> 10), then the quantity vi − npi is distributed asymptotically normally.

npi

Let there be some χ 2p , for which χ 2 > χ 2p with the probability p in the

event of n– 1 degrees of freedom, then it should be taken that the given sample exhibits a significant difference from the hypothetical distribution,

and then the hypothesis Н0 is rejected. Otherwise (χ 2 < χ 2p ) , the

hypothesis is accepted. According to this rule, the probability of a correct hypothesis to be rejected is equal to p.

t–criterion (Student’s)

This criterion is normally used to check if a calculated average value differs from the quantity preset (X = μ ).

To this end, the following criterion is used:

195

If the hypothesis is just, then the quantity t obeys to Student’s distribution with the (n– 1) degree of freedom.

Example. Let there be a group of people growing as follows: 160, 160, 167, 170, 173, 176, 178, 178, 181 and 181.

Let hypothesis Н0 consist in that these values are distributed by normal law with the average value of 167 cm and the hypothesis Н1 in that `Х > 167.

Solution:

10

∑xi

samples differ significantly.

When two variances are compared, it is convenient to check the relation:

and compare this quantity with that in the table for the number of the degrees of freedom ν1 and ν2 and the significance level р.

196

Example. Let there be data from three laboratories (Table 4.4):

i=1

measurements in the i laboratory, and k is the number of laboratories.

The formulas to calculate the number of the degrees of freedom and the variances are given in Table 4.5.

197

∙proper use of tamper indicating devices;

∙the numbers on tested items which should coincide with database.

To have a representative sample, one should be aware of how the characteristic of interest is distributed inside the set:

∙ uniformly throughout the set; ∙ uniformly within clusters;

∙ uniformly inside layers; ∙ not known.

Each sampling test program includes the following items. 1. Purpose of sampling test.

2. Analysis of the set to be tested and characteristics thereof. 3. Analysis of constraints and statistical concerns.

4. Analysis of constraints and nonstatistical concerns.

5. Calculation of sample size.

6. Selection of sampling strategy.

Let us take a closer look at the above items.

Purpose of sampling test:

∙check of earlier measurements;

∙determination of the NM quantity as described in the given inventory listing;

∙check of database records and the inventory listing for conformity;

∙finding out if tamper indication devices are properly applied.

Identification of the set to be tested. When analyzed, the set should

have its sample-affecting characteristics identified, so one shall find out:

∙if the set is homogeneous in terms of the given characteristic;

∙if not, if the set layers are homogeneous;

∙how the items of interest are stored;

∙if radiation safety concerns exist.

Statistical characteristics. Qualitative (discrete) characteristics:

∙set size;

∙distribution of the given characteristic inside the set;

∙required significance level;

∙admissible number of defects.

So, for example, a study is required to secure with a 95% probability that not more than 1% of the set elements are defective.

Quantitative (continuous) characteristics:

∙what loss, if any, should be regarded significant;

∙estimate uncertainty;

199

∙ permissible number of type I and II errors (type I error is a false loss detection (the true hypothesis is rejected), type II error is omission of a real loss (a false hypothesis is accepted)).

The foregoing determines to some extent the size of the desired sample.

Nonstatistical constraints:

a)regulatory requirements;

b)safety and security requirements;

c)constraints determined by limited physical resources, finding included;

d)time constraints.

The sample size is determined by the following parameters:

∙size of the set to be tested;

∙maximum permissible number of defects;

∙significance level.

An inspection to check the system of tamper indicating devices (TID) suggests a check for two reliability conditions.

Condition 1. The recording system should show the exact location and identification of at least 99% of the TIDs.

Condition 2. The TIDs should be properly applied in not less than 95% of cases.

For a sampling test, the confidential probability is taken as 95%. Example. Let us consider a set of 2000 items. We shall try to determine

the minimum sample size at which one can check with a probability of 95% (i.e. α = 0.05) the second condition: not more than 5% of the elements (i.e. not more than 100) have defects.

The function of distributing the enumeration probability for х defective elements in a sample of n elements from a set consisting of N items and having only D defective items is described by a hypergeometric distribution (4.21):

200