
Крючков Фундаменталс оф Нуцлеар Материалс Пхысицал Протецтион 2011
.pdfD(x1 + x2... + xn ) = D(x1) + D(x2 ) + ... + D(xn ) = nσ 2 , |
(4.8) |
||||||||
x1 |
+ x2... + xn |
= |
1 |
|
+ x2... + xn ) = |
σ 2 |
(4.9) |
||
D |
|
|
|
|
D(x1 |
. |
|||
|
n |
|
|||||||
|
|
|
n |
|
n |
|
|||
Distribution function
A random quantity can be considered to be fully characterized if for any value х the distribution function F(x) is known:
F(x) = P(X<x). |
(4.10) |
Unlike the distribution law that unambiguously relates the values р and х, the distribution function gives a random quantity a somewhat different and more general characterization. The probability that a random quantity will assume any value satisfying the inequality x1 ≤ x < x2 , is equal to the increment of its distribution function on this interval:
P(x1 ≤ x < x2 ) = F (x2 ) − F (x1) .
Continuous random quantity
We shall introduce the concept of continuous random quantity.
Random quantity is called continuous if its distribution function is everywhere continuous with its derivative (to the exclusion of the finite number of points on a finite interval).
Probability density of continuous random quantity |
|
Probability density ϕ(x) for a continuous random quantity |
is its |
distribution function derivative: |
|
ϕ(x) = F '(x) . |
(4.11) |
The probability of a continuous random quantity Х to assume any value in the interval (а,b) is equal to a certain integral of its probability density in the limits of а, b:
161
b
P(a < X < b) = ∫ϕ (x)dx = F (b) − F (a),
a
+∞
∫ϕ (x)dx = 1.
−∞
The probability density ϕ (x) for a random quantity Х distribution function F(x) mutually determine each other. Actually,
x
F (x) = P(−∞ < X < x) = ∫ϕ (x)dx .
−∞
(4.12)
and its
(4.13)
The geometrical interpretation of the formulas at hand is fairly obvious. The distribution curve for a continuous random quantity is called its probability density plot.
The mathematical expectation М(X) for a continuous random quantity:
+∞ |
|
M ( X ) = ∫ xϕ(x)dx . |
(4.14) |
−∞ |
|
The variance D(X) of a continuous random quantity: |
|
+∞ |
|
D( X ) = ∫(x − a)2 ϕ(x)dx, где a = M ( X ). |
(4.15) |
−∞
All earlier found mathematical expectation and variance properties are also just in the event of a continuous random quantity. One example is the
property (4.5) for a continuous random quantity:
+∞
D( X ) = ∫ x2ϕ (x)dx − [M (X )]2 .
−∞
Apart from mathematical expectation and variance, other numerical measures are used that reflect various distribution peculiarities. Consider the following major measures of distribution.
Moments
Special numerical measures of a random quantity are moments around zero and moments around mean. Mathematical expectation and variance are known to be moments, and more precisely, mathematical expectation is the first-order moment around zero, and variance is the second-order moment around mean. All basic distributions relate to the moments of the
162
first two orders (these are parameters of these distributions). If, however, one has to give a detailed characterization to a random quantity, moments of higher orders can be used.
By the moment around zero of the order k we shall mean:
ν k = M ( X k ), |
(4.16) |
and by the moment around mean of the order k we shall mean
μk = M [(X − M (X ))k ]. |
(4.17) |
Median
This is used to indicate to the center for the grouping of a random quantity’s values alongside with mathematical expectation. For a continuous random quantity, median is the boundary left and right of which the random quantity values are with a probability 0.5. For a normal distribution: Ме(Х) = М(Х) = а.
Mode
For a continuous random quantity, mode is the point of the probability density function local maximum. For a normal distribution, Мо(Х) = М(Х)
= а.
Quartiles
Quartiles are boundaries that divide the whole of the distribution into four equally probable parts. There are three quartiles in all. It is obvious that the central quartile is the median.
Quantiles
By the quantile of the level q (or q– quantile) they mean such value xq
of a random quantity with which the distribution function thereof assumes the value equal to q:
F (xq ) = P( X < xq ) = q . |
(4.18) |
163
Some quantiles have special names. It is obvious that the above introduced median is the quantile of the level 0.5, that is, Me( X ) = x0,5 .
The concept of quantile has a close link to the concept of percentage
point. |
|
A 100q% point is understood as quantile |
x1−q , i.e. as such value of the |
random quantity Х that makes the following condition just: |
|
P( X ³ x1−q ) = q . |
(4.19) |
Binomial distribution law
The distribution law for the occurrence х of the event А in n independent tests, in each of which this can occur with the constant probability р, obeys to binomial distribution law, the expression of which is Bernoulli’s formula:
P(x = m) = Cnm pmqn−m , m = 0,1, 2,... , n . |
(4.20) |
The mathematical expectation of a binomially distributed random quantity is equal to np, and the variance is equal to npq:
M(X) = np; D(X) = npq.
Typically, binomial distribution is interpreted as:
·the probability of an event to occur exactly т times in п independent tests (Bernoulli case) provided the probability is constant and equal to р;
·(with a test regarded to be sampling) the probability that a replicate random sample of the size п contains exactly т elements of the given type, given the universe of the size N contains pN elements of the given type.
Hypergeometrical distribution law
A generalization of binomial law is hypergeometrical distribution law:
N1 |
N - N1 |
|
|
m n−m |
|
|
|
|
|
|
|
|
|
P( X = m) = m |
n - m |
|
= |
CN1CN − N1 |
, |
(4.21) |
N |
|
n |
||||
|
|
|
|
CN |
|
|
|
n |
|
|
|
|
|
164
where N ³ n , |
N ³ N1 = pN ; |
|
|
|
|
|
|
|
|
|
||
|
nN1 |
|
nN1 |
(N − N1) |
|
n −1 |
|
|
n −1 |
|||
M ( X ) = |
|
= pn; D(X) = |
|
|
1 |
− |
|
|
= np(1 − p) 1 |
− |
|
. |
N 2 |
|
N 2 |
|
|
||||||||
|
|
|
|
|
N −1 |
|
|
N −1 |
||||
A typical interpretation of hypergeometrical distribution law: Р(Х = т) in (4.21) is the probability that a non-replicate random sample of the size п contains т elements of the given type, if this sampling is done from a universe of N elements in which N1 = pN elements of the given type.
The following passage to the limit is just: it is obvious that if |
N → ∞ |
while п and p = N1 / N remain fixed, the geometrical law |
tends to |
binomial. In fact, a non-replicate sample differs little from a replicate sample if the ratio п / N is small. The given approximation is just if n / N < 0,1.
Note that the mathematical expectation for the relative frequency of the event А in п independent tests, in each of which it may occur with the probability р, is equal to this probability and the variance is equal to pq/n.
Thus, M(X/n) = p, D(X/n) = pq/n. So: |
|
||||
|
|
|
|
|
|
σ = |
pq |
. |
(4.22) |
||
|
|||||
|
|
n |
|
||
Therefore, an increase in the number of tests makes the relative frequency of an event decreasingly less dispersed about this probability.
Poisson’s law
If a random quantity Х is capable of assuming only integer nonnegative
values т = 0, 1, 2, 3,… with the probability: |
|
|
P( X = m) = λme−λ |
, |
(4.23) |
m! |
|
|
where λ is the parameter, it is said to be distributed by Poisson law.
This is the law of rare events, the probability of which (р) is small and the number п is large, say, severe accidents, birth of triplets and so on.
165
Poisson distribution approximates hypergeometrical and binomial when pN → ∞; n → ∞; p → 0 given рп has the finite limit рп = λ. This approximation is normally used if р < 0,1.
The mathematical expectation and the variance for a random quantity distributed by Poisson’s law coincide and are equal to the value of the parameter λ = рп.
Normally distributed random quantities
Most of the experimentally obtained, measured or observed continuous random quantities are distributed by normal law:
ϕn (x) = |
1 |
|
|
− |
(x − a)2 |
|
|||
|
|
|
exp |
|
|
. |
(4.24) |
||
|
|
|
|
2 |
|||||
|
|
|
|||||||
|
σ 2π |
|
|
|
2σ |
|
|
||
|
|
|
|
|
|
|
|||
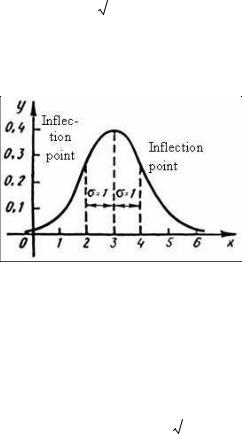
The quantities σ and а are normal distribution parameters. The plot for this distribution is a normal curve or a Gaussian (Fig. 4.2).
Fig. 4.2. Normal curve
A normal curve with the parameters а = 0 and σ = 1 is called standard. The function ϕn (x) has the following properties:
∙it exists at all actual values of the argument;
∙ has the extreme point at х = а, ϕn |
(а) = |
|
1 |
|
; |
|
|
|
|
|
|||
σ |
|
2π |
||||
|
|
|
|
|
||
∙is symmetrical about the axis through х = а;
166
∙has two knee points, left and right of х = а with abscissas, respectively,
x= a − σ and x = a + σ .
It is easy to verify that normal distribution parameters have the meaning of the mathematical expectation and the RMS deviation:
a = M(X) и σ = 
 D( X ) .
D( X ) .
It can be shown that normal curves with coinciding σ are identically shaped and differ just in the maximum coordinate shift. The value of the variance, and more exactly, σ (RMSD), influences greatly the normal curve shape. With a decrease of σ, the curve tends to become “narrower”, extends upwards and gets needle-like; if σ increases, the curve lowers, gets “wider” and approaches the abscissa axis.
If a random quantity Х is distributed normally, then
P(x < X < x |
) = 0,5 × |
|
x - a |
|||
|
Ф |
1 |
||||
σ |
||||||
1 |
2 |
|
|
|||
|
|
|
|
|||
|
x |
2 |
- a |
|
|
||
|
- Ф |
|
|
|
, |
(4.25) |
|
|
σ |
||||||
|
|
|
|
|
|||
|
|
|
2 |
|
x |
|
t 2 |
||
where |
Ф(x) = |
|
|
|
∫exp − |
|
dt is the integral of the probabilities, the |
||
|
|
|
|
||||||
2π |
2 |
||||||||
|
|
|
0 |
|
|
||||
values thereof being tabulated.
The formula (4.25) is simplified if the interval limits are symmetrical about the mathematical expectation:
|
|
|
|
|
|
|
|
|
|
|
|
||||
P( |
|
X − a |
|
≤ )= Ф |
|
. |
(4.26) |
|
|
σ |
|||||
|
|
|
Lognormal distribution
A continuous random quantity Х has a lognormal distribution if its logarithm obeys to normal law. The probability density for lognormal distribution is:
ϕ (x) = |
|
1 |
|
|
− |
(ln x − ln a) |
2 |
|
|
||
|
|
exp |
|
. |
(4.27) |
||||||
|
|
|
|
|
|
||||||
|
σ |
|
2π x |
|
|
2σ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
It can be proved that numerical characteristics of a lognormally distributed random quantity have the following form:
167

M (X ) = a exp(σ 2 / 2), Me(X ) = a,
(4.28)
D(X ) = a2 exp(σ 2 )(exp(σ 2 ) −1).
Lognormal distribution is rather commonly used to describe a distribution of profits, a distribution of impurities in alloys and minerals, the longevity of products in wear and aging conditions and so on.
Distributions relating to normal distribution
In mathematical statistics, the most common distributions are χ 2 (Pearson), t (Student) and F (Fisher) distributions. All these distributions relate to normal distribution. In turn, common use of normal distribution is determined, as we will see, exclusively by the central limit theorem (CLT) (see Section 4.6). Due to being specially important, all above-mentioned distributions are tabulated and contained in various manuals and reference books [3].
Hereinbelow, we have introduced one-dimensional standard normal distribution as a distribution with the mathematical expectation а = 0 and
the variance σ 2 = 1, its density being
ϕ (x) = Ф'(x) = |
|
1 |
|
− |
x2 |
|
|
|
|
|
|
e 2 . |
(4.29) |
||||
|
|
|
||||||
2π |
||||||||
|
|
|
|
|
|
|
||
In a general case, one-dimensional normal distribution is characterized
by the mathematical expectation а and the variance σ 2 . Then, any onedimensional normal distribution can be treated as a distribution of a random quantity:
η = a + ξ 
 σ 2 ,
σ 2 ,
where the random quantity ξ obeys to standard normal law.
Pearson distribution. Let ξ1,...,ξn be independent random quantities distributed by standard normal law. The distribution of the random quantity:
χ 2 = ξ12 + ... + ξn2
168

is called χ 2 –distribution (Pearson distribution) with п degrees of freedom.
χ 2 –distribution has the density
|
|
|
1 |
|
|
|
n |
−1 |
− |
x |
|
|
h(x) = H '(x) = |
|
|
|
|
|
x 2 |
|
e 2 (x > 0) , |
(4.30) |
|||
|
n |
n |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
2 2 |
|
|
|
|
|
||||||
|
Г |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|||
where Г(n) is a gamma function. |
|
|
|
|
|
|
|
|
||||
Further, the following property will be useful to us. Let |
ξ1,...,ξn be |
|||||||||||
independent normally distributed random quantities with the identical parameters а and σ 2 . We shall assume that
η= 1 (ξ1 + ... + ξn ) . n
Then the random quantity
χ 2 = |
1 |
[(ξ1 −η)2 + ... + (ξn −η)2 ] |
(4.31) |
|
σ 2 |
||||
|
|
|
has the χ 2 – distribution but with п– 1 degrees of freedom.
There is one more interpretation (case) of Pearson distribution. Let п independent tests be conducted (polynomial case or Bernoulli case), in each of which one of the events Аi (I = 1,…, L) may occur with the probability рi. Let us denote the number of the occurrences of the event Аi by тi. Then it follows from the multidimensional analog of the Moivre-Laplace integral theorem that the random quantity:
χ 2 = |
(m − np ) |
2 |
+ ... + |
(m |
L |
− np |
L |
)2 |
|
|
1 |
1 |
|
|
|
|
, |
||||
np1 |
|
|
|
|
npL |
|
|
|||
|
|
|
|
|
|
|
|
|
||
with n → ∞ , is asymptomatically distributed by χ 2 |
law with L – 1 degrees |
|||||||||
of freedom. |
|
|
|
|
|
|
|
|
|
|
t–distribution. Let ξ and χ 2 |
be independent random quantities, ξ being |
|||||||||
distributed by standard normal law, and χ 2 having a Pearson distribution
169

with п |
degrees of freedom. The distribution |
of |
the |
random |
quantity |
||||||||||||||||
τ = ξ / |
χ 2 / n |
is called a t–distribution with |
п degrees of freedom (Student |
||||||||||||||||||
distribution). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
This distribution has the density |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
− |
n+1 |
|
|
||||
|
|
|
1 |
|
|
Г |
|
|
|
|
|
|
|
x |
2 |
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||
|
|
t(x) = T '(x) = |
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
, |
(4.32) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
π n |
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
where Г(т) is the gamma function.
Let ξ1,...,ξn be independent random quantities similarly distributed by normal law with the average а. Let us assume that
η = |
1 |
(ξ1 + ... + ξn ) , ς = (ξ1 −η)2 + ... + (ξn −η)2 . |
||||||||
|
||||||||||
|
n |
|
|
|
|
|
|
|
|
|
Then the random quantities ζ è η |
are independent and the random |
|||||||||
quantity |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(η − a) |
||||
|
|
|
τ = |
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ς |
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n −1 |
|
|
|
has a t–distribution with п – |
1 degrees of freedom. |
|||||||||
F–distribution |
relates to Pearson distribution as follows. Let χ12 , χ22 be |
|||||||||
two independent |
random |
quantities |
having an χ 2 distribution with |
|||||||
n1 and n2 degrees of freedom respectively. The distribution of the random quantity
|
ϖ = |
n2χ12 |
|
|
n1χ22 |
||
|
|
||
is |
referred to as F– distribution (Fisher distribution) with the parameters |
||
n1 |
and n2 . The density of the F–distribution is: |
||
170
