Крючков Фундаменталс оф Нуцлеар Материалс Пхысицал Протецтион 2011

Covariance and correlation ratio

If the random quantities Х and Y are dependent (or we know nothing about the dependence of these), the variance of the sum or of the difference should be written as follows:

D(X±Y) = D(X)+D(Y)±2M((X– M(X))(Y–M (Y))) = = D(X)+D(Y)±2M(XY)– M(X)M(Y).

It is obvious that for independent quantities: M(X– M(X))(Y–M (Y)) = = M(XY)– M(X)M(Y) = 0.

For dependent quantities, we introduce the concept of covariance (joint variance) for the random quantities Х and Y:

cov(X,Y) = M((X– M(X))(Y– M(Y))) = M(XY)– M(X)M(Y). (4.34)

And the variance in this case is determined as

Note that, essentially, covariance is the joint first-order moment about mean.

It follows from (4.34) that covariance has the following property:

cov(X,X) = M((X– M(X))(X– M(X))) =D(X).

In fact, covariance (covariance ratio) is to a certain degree a measure of the relationship (dependence) between some random quantities since it possesses the following properties:

∙for independent random quantities, the covariance is equal to zero;

∙it is positive for the random quantities Х and Y tending to vary unidirectionally, and it is negative for those showing the opposite trend.

171

However, this ratio is capable of assuming values across the number axis so it is not quite good and convenient for measuring the dependence degree. More convenience in this sense is provided by standardized covariance ratio (the so-called correlation ratio) which is normally introduced as

In fact:

∙for the independent random quantities x and y, ρ(x,y) = 0, because the covariance is equal to zero;

∙for linearly dependent random quantities | ρ | = 1;

∙ for the rest, the correlation ratio varies in a range of –1 to +1 (–1< ρ <+1).

Let us note that the closer | ρ | is to 1, the more reasons one has to treat X and Y as linearly dependent.

Strictly speaking, if the correlation ratio is zero, this does not always mean independence of random quantities. In this case, they say the quantities are uncorrelated (or do not correlate). Independence implies strictly lack of correlation and it is not always the case vice versa. However, it has been strictly shown that the properties of lack of correlation and independence are equivalent for normally distributed random quantities.

Therefore, one can characterize the function of random quantities or a multidimensional random quantity only by a covariance matrix, say, for the case X1 and X2:

Law of large numbers

It has long been observed that the arithmetic-mean value for numerical characteristics of random events (relative frequency) in a great number of

172

such similar events tends to vary to a certain extent. On the average, a dependence shows itself which is inherent in the essence of phenomena, this having the influence of some factors that randomized single observation results cancelled therein.

Chebyshev inequality

Chebyshev inequality is a mathematical from of the law of large numbers: the probability that a deviation of random quantities from its mathematical expectation will exceed ε > 0 in the absolute magnitude, and will be no

greater than the relation of its variance to ε 2 .

Let Х be a random quantity, а its mathematical expectation and D(х) the variance, then

Chebyshev inequality gives a nontrivial estimate to the probability of the event Х - а £ e only where D( X ) < ε 2 , the estimate being trivial and not informative in other cases.

Conclusion. Where independent random quantities have identical mathematical expectations equaling а, the variance is limited to one and the same constant с, and the number is great, then for ε > 0 , the probability that the arithmetic mean of these random quantities will deviate from а is arbitrarily close to unity:

This conclusion makes the simplest law of large numbers. Practically, this means that the arithmetic mean of the measurement results is taken for the approximated value of an unknown random quantity. Given that the number of measurements is rather great, this will prove the practical reasoning which is important in terms of (4.39). The equality of the mathematical expectation for the same quantity а is required to show the absence of the so-called systematic component of measurement error.

173

Limit theorems

If random quantities are many and satisfy some quite general conditions, then, whatever distribution these have, it is practically certain that the arithmetic mean thereof has an arbitrarily small deviation from the constant or the arithmetic mean of the mathematical expectations thereof, i.e. is practically a constant.

Thus, a common sampling technique making it possible to conclude on the universe based on the limited sample test findings, gets a rationale from the law of large numbers:

the number of grains in a sample (measure), п, is enough to infer the size of the whole grain batch, N, from; the number of the tested items (e.g. fuel assemblies), п, is enough to infer the size of the whole FA batch, N, from; i.e. enough for the law of great numbers to manifest itself with a satisfactory accuracy, though n < N, but n is rather great and the law works.

It can be shown that the sum of any finite number of normally distributed random quantities is normally distributed. Then, if independent random quantities are not distributed normally or are actually distributed in an unknown fashion, then it turns out that they may have some rather soft restrictions imposed on them such that the sum thereof will be distributed normally. This makes the essence of the so-called limit theorems. A form of central limit theorems is Lyapunov theorem [3].

4.2. Basic statistical requirements to NM A&C systems

Upgrades to and evolutions of NM accounting and control systems suggests a greater role of measurements in determining and verifying NM inventories. One can conclude on NM inventories against the background of uncertainties, that are inherent in measurements, only through using statistical methods and employing statistical criteria [4].

We shall consider the major uncertainties inherent in accounting and control of NM:

∙uncertainty inherent in applicable measurement methods;

∙uncertainty inherent in items to be measured;

∙uncertainty inherent in calculation techniques;

∙uncertainty due to the sampling procedure used;

∙uncertainty inherent in “documented” NM data.

Let us underline again that measurements are decisive to all operations on checking the presence and integrity of NM. Of crucial importance in this is to achieve the needed level of measurement accuracy to ensure the level

174

of nuclear material control one desires. One of the most important tasks of MS is to analyze uncertainties, estimate measurement errors and search for ways to reduce these. Test measurement results normally deviate from the value declared for the measured characteristic of the NM under control. The cause of a deviation may be a statistically estimated uncertainty (measurement error) or the actually observed difference between the value measured and the one declared. The final conclusion with respect to the cause of the deviation can be made only using a statistical analysis based on accepted statistical criteria.

The need for statistical criteria to be used in inspections also arises due to limited time and funds. Production processes have to be stopped for the inspection, this leading to an economic loss. So, in such cases, sampling checks are done with only some of the items measured. MS is also employed to have the sample size and sequence rationally planned.

The prime objective of NM accounting and control (confident traceability of NM) may be achieved only through an extensive use of statistical and probabilistic methods.

The framework for both determining the inventory of NM in an MBA and detecting anomalies in using NM is formed by NM physical inventory takings. NM physical inventory takings involve audits of accounting data and measurements of the NM quantities in the material balance areas, material balance closing, determination of inventory difference (ID) and estimation of the ID error for each NM.

Absence of anomalies in using NM and of deficiencies in the NM accounting and control system is concluded on based on statistical criteria, that is, statistical guidelines for making decisions from the ID quantity obtained, the ID error and the quantities of the probabilities as set by the guidelines, and detection of a shortage/surplus in NM threshold quantities. We shall highlight again the principles of NM accounting and control that define the statistical requirements:

∙NM shall be subject to state accounting and control starting with the smallest quantities;

∙NM classification depends on the quantity, type and form of the NMcontaining product;

∙onsite MBAs are organized;

∙key measurement points (KMP) are identified in each MBA;

∙NM has access controls (AC) applied thereto to extend the confidence of earlier measurements;

175

∙NM is accounted for based on measurements of NM quantity data and attributes;

∙there may be accounting and verifying measurements.

∙Statistical criteria are used to:

∙find anomalies by verifying measurements;

∙perform sample checks of access indicating devices in between inventory takings;

∙find anomalies in NM accounting via analyzing the inventory difference;

∙find anomalies in NM transfer operations;

∙set the upper limit for the uncertainty of verifying measurements of NM samples;

∙verify the confidence of accounting records.

Let us specify and define respectively some of the special concepts.

Rule of practical certainty and confidential probability

If an event is unlikely in some conditions, then, given these conditions are fulfilled once, one can be certain that the event will not occur. So, in practice, the event in question can be considered impossible. Practically, however, one cannot derive such upper boundary of the probability, at which some events can be believed to be impossible. The scale of the effects from the events of interest is also an important factor to note. We will refer to the probability, we have decided to neglect herein, as the significance level.

Statistically, the significance level is normally assumed as:

~0.05 in pre-estimates;

~0.001 in final conclusions.

The concept of significance level has a close link to the concept of confidential probability: by confidential probability we will mean such probability α at which events with the probability 1– α can be considered impossible.

Confidence interval

We shall introduce the concept of confidence interval which is closely associated with the concept of confidential probability we have introduced hereinabove.

Due to the randomness of measurement data, one cannot set fairly narrow limits, the estimation error (i.e. the deviation of the estimate from

176

the characteristic under estimation) would securely remain in. This leads to a problem of defining such limits beyond which estimation error would fail to fall with the specified probability. For example, if Р is the estimated probability of the event р, one needs to set, based on the same measurement data, such boundary for the potential deviations of Р from р that would not be exceeded by the error modulus P − p with the specified preset

probability α. This boundary will be also random due to the randomness of measurement data.

So the point is to find, from measurement data, such random interval (i.e. an interval with random boundaries) that would contain with the specified probability α an unknown value of the probability р. Such random interval, as determined in full by the measurement results, is referred to as the confidence interval for the given characteristic, this corresponding to the confidential probability α. The quantity 1 − α is referred to as the estimate deviation significance level.

For every quantity, NM weights are found by accounting measurements (or, if these cannot be done, using experimental estimates based on the earlier experience of operation) with documenting the recorded average NM weight values, the confidence interval value for the random error of the NM weight measurement and the boundaries of the residual systematic measurement error based on the confidential probability of 0.99.

These values can be used in accounting procedures (physical inventory takings, NM transfers and so on) only where the confidence thereof from the time of determination to the application time was extended through a proper use of ACs and verified in the process of the accounting procedure by measurements of the NM quantitative parameters and/or the NM attributes (i.e. verifying measurement data).

Error confidence boundaries for the measurement data will be referred to by us as the highest and the lowest measurement error values that confine the interval within which the sought-after measurement error remains with the specified probability interval.

Accounting measurements are measurements of the quantitative characteristics and attributes of NM, items and products, the data from which, including measurement errors, are entered on accounting records as certified values. The subsequent accounting measurement invalidates the preceding measurement result.

Verifying measurements are measurements the data of which is used to verify all or some of the quantitative characteristics and/or attributes of NM, items or products as obtained in earlier accounting measurements and

177

stored confidently thereafter by way of applying NM access controls. Where the difference in the quantities of the measured quantitative characteristic for the verifying and the accounting measurement is not in excess of its standard measurement errors, the certified value of the characteristic is accepted. Otherwise, the discrepancy is investigated and accounting measurements of this NM are done. Verifying measurements can be done by sampling or for all NM.

The extent to which verifying measurements shall be applied is determined depending on the extent to which ACs are used and on the AC status check data, given the probabilities of detecting a shortage/surplus in the threshold amounts of each NM.

The statistical significance of the difference in the accounting and verifying measurement data for the quantitative variables of NM, items and products is determined given the confidential probability of 0.99. If a statistically significant difference is found between the accounting and verifying measurement data, this is reported to the MBA and nuclear facility administration with special investigations undertaken to find out the cause for the difference. As required, new accounting measurements are done and the accounting records are updated respectively.

Statistical criteria for anomaly detection

Each measurement of the NM quantity involves a certain error which leads to a discrepancy between the shipper and the receiver data, and between the results obtained by the inspector and the existing accounting records. A decision on if the discrepancies detected shall be accepted or not is made based on a statistical analysis thereof.

If the material balance period (MBP) preceding the given inventory taking had accounting measurements done in the MBA for the given nuclear material in production, receipt, processing or shipment, or done in the course of the inventory taking, the criterion for detecting anomalies in using the given NM shall be a modulus that exceeds the inventory difference or its threefold root-mean-square error, or any of the following quantities with the confidential probability of 0.95:

∙2% of the total quantity of the given NM booked and of all increases in the quantity thereof over the MBP – for commercial nuclear facilities;

∙3% of the same quantity – for test nuclear faciliti es;

∙3 kg – for plutonium and uranium–233 for the MBAs t hat contain NM of categories I and II;

178

∙ 8 kg – for uranium–235 for the MBAs that containing NM of categories I, II and III;

∙70 kg for uranium–235 – for uranium enriched at bel ow 20%.

If no accounting measurements for the given NM were conducted in the course of the inventory taking during the MBP and the confidence of the preceding accounting measurement data was ensured through the use of ACs, the conclusions with respect to the absence of accounting and control anomalies shall be made based on the sampling verifying measurement data, the volume of this verifying measurement to be determined from the following values of the NM threshold quantities for detection of an NM shortage/surplus and the probabilities of detecting a shortage/surplus of the given threshold quantity.

For NM of categories I, II and III, the threshold quantities are:

∙3 kg – for plutonium and uranium–233;

∙8 kg – for uranium–235;

∙in the case of uranium enriched at below 20% (category 4), the threshold quantity is 70 kg for uranium–235.

The probability of detecting a shortage/surplus of the NM threshold quantity for calculating the verifying measurement sample size is presented in Table 4.1.

Table 4.1

Probability of the NM threshold quantity shortage/surplus detection

The operator-level physical inventory taking procedures are based on a series of actions:

∙comparison of accounting records and reports;

∙check of the AC status;

∙accounting and verifying measurements of the Nm physical inventory;

∙determination of the shipper/receiver data difference;

∙estimation of random and systematic measurement errors, including in receipts and shipments;

∙estimation of process discards;

179

∙ determination of the ID and its random and systematic error for each NM.

The NM parameter measurement data as obtained at earlier process stages can be used for the physical inventory taking only where auxiliary engineered controls (ACs, seals, etc.,) are applied to NM. If NM exists in broad varieties and/or large quantities, one may use statistical samplings to verify the data of online process records and reports respectively. To determine the size of a random sample, one needs to proceed from the requirement of detecting a defect (damage, removal or substitution) in at least one of the above means with the probability of below 0.95.

If no NM accounting and control anomaly is found in an NM balance analysis, the booked inventory of NM in the MBA is accepted as the NM inventory in the MBA as of the beginning of the next material balance period.

4.3. Errors, their models and sources

The knowledge about physical inventories, receipts and shipments of NM requires weight, volume, uranium concentration and enrichment data. One can get this knowledge only by measurements.

Types of measurements

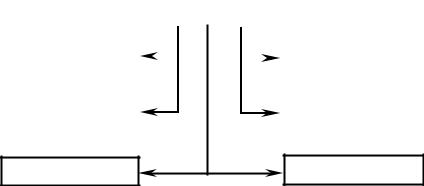
Fig. 4.3 gives a classification of measurements.

Fig. 4.3. Classification of measurements

180