
Красников Моделирование физических процессов с исползованием 2012
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»
Г.Е. Красников, О.В. Нагорнов, Н.В. Старостин
Моделирование физических процессов с использованием пакета
Comsol Multiphysics
Рекомендовано УМО «Ядерные физика и технологии» в качестве учебного пособия
для студентов высших учебных заведений
Москва 2012
УДК 519.85(075) ББК 22.18я7 К78
Красников Г.Е., Нагорнов О.В., Старостин Н.В. Моделирование физических процессов с использованием пакета Comsol Multiphysics: Учебное пособие. М.:
НИЯУ МИФИ, 2012. 184 с.
Предназначено для изучения среды математического моделирования Comsol Multiphysics. В пособии подробно рассматриваются ключевые методы работы с данной системой и разбираются конкретные типовые задачи. Также в книге содержится руководство по математическому программированию на Comsol Script и особенности взаимодействия пакета Comsol Multiphysics с системой Matlab.
Данное пособие – первое руководство по Comsol Multiphysics на русском язы-
ке.
Полезно для студентов 3 и 4 курсов, изучающих курс математического моделирования.
Подготовлено в рамках Программы создания и развития НИЯУ МИФИ.
Рецензент д-р физ.-мат. наук, проф. Н.А. Кудряшов (НИЯУ МИФИ)
ISBN 978-5-7262-1688-1 |
© Национальный исследовательский |
|
ядерный университет «МИФИ», 2012 |
Редактор Т.В. Волвенкова
Подписано в печать 15.11.2011. Формат 60х84 1/16
Уч.-изд. л. 11,75. Печ. л. 11,5. Тираж 120 экз.
Изд. № 1/57. Заказ № 21.
Национальный исследовательский ядерный университет «МИФИ». 115409, Москва, Каширское ш., 31
ООО «Полиграфический комплекс «Курчатовский». 144000, Московская область, г. Электросталь, ул. Красная, 42
ВВЕДЕНИЕ
Программа Comsol Multiphysics 3.5a (FEMLAB) – математиче-
ский пакет, предназначенный для численного решения задач различных областей физики. Пакет основан на методе конечных элементов, с помощью которого производятся все вычисления. Во время выхода версии 3.2, компания Comsol переименовала пакет
FEMLAB в Comsol Multiphysics. В настоящей работе для упроще-
ния будет использоваться как новое, так и старое названия. Программа Comsol Multiphysics – это мощное средство для решения сложных задач, сопровождаемых большими объёмами вычислений. Возможность решать тот или иной класс задач реализована в виде специальных прикладных режимов, при загрузке которых автоматически выбирается нужная система уравнений, в которой необходимо только задать коэффициенты и граничные условия. В пакете FEMLAB доступны для решения классы задач электростатики, электродинамики, электромагнетизма, акустики, теплопереноса, теории упругости, гидродинамики, а также классические дифференциальные уравнения, такие как уравнение Шрёдингера, уравнение Гельмгольца, уравнение теплопроводности, волновое уравнение и другие. В вышеуказанных классах задач допускается решать, стационарные, временные задачи, задачи на собственные значения,
атакже параметрические задачи.
1.МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
1.1. Теоретическое введение
Рассмотрим следующую задачу Коши для обыкновенного дифференциального уравнения:
u''(x) = q(x);
x [a;b]; (1.1)
u(a) = 0;u'(b) = 0;
3
где q(x) – произвольная известная функция от x. В общем виде уравнение не решается аналитически. Однако можно упростить задачу, потребовав выполнения решения уравнения не на всей непрерывной области [а; b], а лишь на определённом наборе промежуточных точек. Сделаем это следующим образом.
Разобьём область решения [а; b] на конечное число отрезков
[x ; x |
], на каждом из которых выберем базисную функцию ϕ |
i |
, |
по |
|
i i+1 |
N |
|
|
. |
|
|
|
|
ϕ |
||
которым бы можно было разложить исходную функцию u = ∑u |
|||||
|
i=1 |
i |
|
i |
|
|
|
|
|
||
Функции должны быть такого вида, чтобы по ним можно было разложить любую функцию u(x), а также чтобы они образовывали базис на области решения, т.е. удовлетворяли условию: (ϕi ;ϕj ) = 0 .
Наиболее простыми для расчётов являются кусочно-линейные функции в виде треугольников:
|
x − xi−1 |
||
|
|
|
|
ϕi |
xi − xi−1 |
||
= |
− x |
||
|
xi+1 |
||
|
|
|
− xi |
|
xi+1 |
||
; x [xi−1 ; xi ]
. |
(1.2) |
; x [xi ; xi+1 ]
Для упрощения вычислений выберем все элементы одинакового размера h.
R(x) =u''(x) −q(x) =0 – невязка исходного уравнения.
Для решения задачи, необходимо минимизировать её по методу Галёркина, умножая скалярно R(x) на каждую из базисных функций:
(R(x);ϕi (x)) = ∫b |
R(x)ϕi (x)dx = ∫b (u''(x) − q(x))ϕi (x)dx = 0; |
(1.3) |
a |
a |
|
i 1..N. |
|
|
Преобразуем каждый интеграл по отдельности.
4

b |
b |
∫u' ' (x)ϕi (x)dx = ∫[(u' (x)ϕi (x))'−u' (x)ϕi ' (x)]dx = |
|
a |
a |
b
= u' (x)ϕi (x) ba −∫u' (x)ϕi ' (x)dx.
a
Первое слагаемое равно нулю, поскольку все базисные функции обращаются в 0 на концах отрезка. Второй интеграл можно разложить на две части
b |
|
|
|
xi |
|
1 |
|
|
xi +1 |
|
1 |
|
|
|
∫ |
u' (x)ϕi ' (x)dx = |
∫ |
u' (x) |
dx + |
∫ |
u' (x)(− |
)dx = |
|||||||
h |
|
|||||||||||||
|
|
|
|
|
|
|
h |
|||||||
a |
|
|
|
xi −1 |
|
|
|
|
xi |
|
|
|
|
|
= |
1 |
(ui −ui−1 −(ui+1 −ui )) |
= − |
ui+1 −2ui +ui−1 |
. |
|||||||||
|
h |
|
||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
||
Таким образом получаем систему линейных алгебраических уравнений с матрицей следующего вида:
|
1 |
|
0 |
0 |
|
0 |
|
||
|
− 1 |
|
2 |
|
− 1 |
|
.. |
|
|
|
h |
h |
h |
|
|||||
.. |
|
.. |
.. |
|
|||||
|
.. |
|
|
||||||
|
|
|
.. |
− 1 |
|
2 |
|
|
|
.. |
|
h |
h |
||||||
|
0 |
|
0 |
0 |
|
||||
|
|
|
− 1 |
h |
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
u1 |
|
|
f1 |
|
|
|
|
|
|
|
|
|
|
|||||
.. |
|
|
u2 |
|
|
f2 |
|
|
|
|
|
|
|
|
|
|
|
||||
.. |
|
|
|
|
= |
.. |
|
, |
(1.4) |
|
|
.. |
|||||||||
− 1 |
|
|
|
|
|
f N |
|
|
|
|
|
|
h uN |
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
h |
uN +1 |
|
|
f N +1 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
где, fN +1 = f1 = 0; fi = ∫b q(x)ϕi (x)dx;i = 2..N.
a
Решив систему методом прогонки, получим коэффициенты u1...uN +1, которые задают исходный вид функции u(x) на опреде-
лённом наборе точек. При N → ∞численное решение будет стремиться к точному.
5

Основное положение метода конечных элементов – переход от решения уравнения на непрерывной области, к требованию выполнения системы уравнений на ограниченном числе точек.
Уравнение (1.3), означающее равенство невязки нулю, является сла-
бой формой дифференциального уравнения. Оно означает выполнение уравнения на определённом наборе точек.
В случае задачи двух переменных, в качестве конечных элементов стоит выбрать шестигранные пирамиды, как показано на рис.1.1, 1.2. Линейная базисная функция будет иметь вид шестигранной пирамиды с вершиной в центре элемента (xi;yi).
Вне элемента функция равна нулю. Далее раскладываем искомую функцию по базису:
|
|
|
ϕ(1) |
= |
|
|
y − y j−1 |
;(x, y) S |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
ij |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y − y j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
i+1/ 2 |
− x |
|
|
−1/ 2 |
|
|
|||||||
|
|
|
ϕij(2) |
= |
( |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
);(x, y) S2 |
|||||
|
|
|
|
a |
|
|
|
|
|
|
|
b |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
xi+1 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(3) |
= |
|
|
|
;(x, y) S3 |
|
|
|||||||||||||
|
|
|
ϕij |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
yi+1 − y |
|
|
|
|
|
|
|
|
|
(1.5) |
||||||
ϕ |
ij |
= |
ϕ(4) |
= |
|
;(x, y) S |
4 |
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
ij |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y j+1/ 2 |
− y |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
− x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ϕ(5) |
= |
( |
|
|
i−1/ 2 |
|
+ |
|
|
|
);(x, y) S |
5 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
ij |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x − xi−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(6) |
= |
|
|
|
;(x, y) S6 |
|
|
|||||||||||||
|
|
|
ϕij |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕij = 0;(x, y) S |
|
|
|
|
|
|
|||||||||||||||
6

N M
u(x, y) = ∑∑αijϕij (x, y) .
i=1 j=1
Метод конечных элементов можно распространить на систему дифференциальных уравнений. В этом случае необходимо разложить каждую искомую переменную.
Представленные выше элементы являются элементами первого порядка или линейными элементами. Значения функции вычисляются только на узлах элемента. Базисные функции
имеют линейный вид. Помимо этих элементов существуют элементы второго, третьего и более высокого порядков. Вместо линейных функций на них используются параболические, кубические функции и функции более высоких порядков. Значения вычисляются не только в узлах элемента, но и на его ребрах. Разложение искомой функции на элементах второго порядка имеет гораздо более сложный вид, чем (1.2). Использование элементов первого порядка возможно, только если оператор L[u] содержит производные только первого порядка. При наличии производных третьего и более высоких порядков в уравнении необходимо использовать элементы соответствующих порядков.
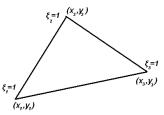
Вместо шестиугольных элементов в МКЭ могут также использоваться треугольные (рис. 1.3, 1.4).
При использовании таких элементов следует перейти к новым переменным ξ1;ξ2;ξ3. Переход осуществляется следующим образом:
7
1 1 1 |
|
ξ |
|
1 |
|
|
||||
|
x2 |
x3 |
|
|
1 |
|
|
|
|
|
x1 |
|
ξ2 |
|
= x |
. |
(1.7) |
||||
y |
y |
2 |
y |
|
ξ |
3 |
|
y |
|
|
1 |
|
3 |
|
|
|
|
|
|
||
Необходимое условие на новую систему координат: ξ1+ξ2+ξ3=1 В новых координатах функция раскладывается следующим об-
разом:
u(x, y) = u(x1, y1 )ξ1 +u(x2 , y2 )ξ2 +u(x3 , y3 )ξ . |
(1.8) |
Разбиение на треугольные элементы (триангуляция) используется в системе FEMLAB.
1.2.Виды конечных элементов
Внекоторых случаях влияние на решение задачи может оказывать выбор базисных функций. Рассмотрим основные типы таких функций.
Лагранжевы элементы – Наи-
более часто используемые базисные функции в FEMLAB. Лагранжев элемент k-го порядка задаёт значение функции на границах элемента, а также на k точках самого элемента.
Например, лагранжев элемент второго порядка задаёт значения функции на всех узлах конечного элемента, а также на середине каждой стороны элемента. Подобная постановка условия позволяет считать производные величины u второго порядка по пространственным координатам.
Лагранжевы элементы второго порядка позволяют решать подавляющее большинство дифференциальных уравнений. В случае, если уравнение содержит производные более высоких порядков, следует выбирать порядок элементов, соответствующий максимальной степени производной в уравнении.
8
Аргирисовы элементы. При аппроксимации переменной лагранжевыми элементами возможны ситуации, когда первые производные на границах между элементами будут бесконечны. В некоторых уравнениях это может быть серьёзной проблемой для решения. В этом случае можно использовать аргирисовы элементы, которые задают конечные производные на границах и вторые производные в углах элемента. На каждом элементе искомая функция u аппроксимируется полиномом 5-й степени в локальных координатах ξ.
Аргирисовы элементы доступны только на треугольных или тетраэдных (3D-случай) сетках.
Эрмитовы элементы. Эрмитовы элементы сходны с элементами Лагранжа за тем исключением, что в углах элемента определяются непосредственно не значения функции, а определяются лишь значения первых производных. Во внутренних точках ребра элемента, как и в случае лагранжева элемента, определяются значения функции. Минимальный возможный порядок эрмитова элемента k=3.
Пузырьковые элементы. Пузырьковые элементы (bubble elements) называются так благодаря своей форме. На границе области, тестовая функция обращается в ноль, а в центре элемента достигает максимума. Элементы доступны на любых сетках.
Помимо вышеперечисленных, в некоторых прикладных режимах в системе FEMLAB используются следующие элементы: векторные, роторные, дивергентные, дискретные.
2. НАЧАЛО РАБОТЫ С FEMLAB
2.1. Установка
Пакет Comsol Multiphysics устанавливается с четырёх дисков. При автоматическом запуске первого диска появляется следующее окно (рис. 2.1):
9
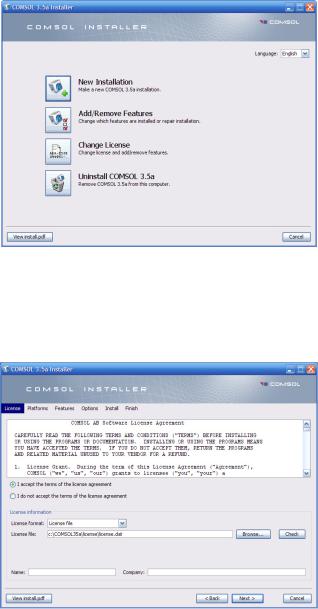
Рис. 2.1. Начало инсталляции Comsol Multiphysics 3.5a
Выберем пункт New Installation. Следующим этапом осуществляется установка лицензии программы (рис. 2.2). Лицензия к программе может поставляться в виде специального лицензионного кода, либо содержаться в файле.
Рис. 2.2. Выбор лицензии для программы
10
