
Красников Моделирование физических процессов с исползованием 2012
.pdf3.5. Решение задач строительной механики
3.5.1. Теоретическое введение
Строительная механика – наука, которая изучает прочность, жёсткость и устойчивость твёрдых конструкций. Именно строительная механика положила начало созданию метода конечных элементов, и в ней он нашёл своё наибольшее распространение. Строительная механика основывается на уравнениях теории упругости. Основной величиной, которая характеризует тело, подвергающееся деформации, является тензор деформаций:
ε |
|
= |
1 |
|
∂u |
+ |
∂u |
|
|
, |
|
|
|
i |
|
k |
|||||
|
2 |
∂x |
|
|||||||
|
ik |
|
|
|
∂x |
|
|
|||
|
|
|
|
|
k |
|
|
i |
|
|
где ui – деформация тела вдоль i-й координаты. В трёхмерном пространстве компоненты тензора εik будут иметь вид:
|
= |
∂u |
;εy |
= |
∂v |
;εz |
= |
∂w |
; |
||
εx |
∂x |
∂y |
∂z |
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
∂u + |
∂v |
|
|
|
= 1 ∂u + ∂w ;εyz |
|||
|
|
;εxz |
|||||||||
εxy = 1 |
|
||||||||||
|
|
2 ∂y |
|
∂x |
|
|
2 ∂z ∂x |
||||
|
|
|
|
|
|||||||
= |
1 |
|
∂v |
+ |
∂w |
|
, |
|
|
||||||
|
2 |
|
∂z |
|
∂y |
|
|
где u, v, w – деформации точки вдоль осей X, Y, Z.
Напряжения в среде описываются тензором напряжений σik. Компоненты тензоров деформаций и напряжений связаны между
собой соотношением:
σ = Dε,
где |
|
|
|
|
|
|
|
|
εx |
|
|
σx |
|
|
|
|
|
|
|
|
|
|
|
|
εy |
|
|
σy |
|
|
|
|
|
|
|
|
|
|
|
ε = |
εz |
|
;σ = |
σz |
|
; |
|
2εxy |
2σxy |
||||||
|
|
|
|
|
|
|
|
|
2εxz |
|
|
2σxz |
|
||
|
|
|
|
|
|
|
|
|
2εyz |
|
|
2σyz |
|
||
91
D – матрица жёсткости. Для изотропных, анизотропных, ортотропных материалов она определяется по-разному. Более простой вид имеет обратная матрица к D, называемая матрицей податливости. Для изотропных материалов она имеет следующий вид:
|
|
|
|
1 |
−v |
v |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
−v |
1 |
−v |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
||||||
D |
−1 |
= |
1 |
|
−v −v 1 |
0 |
0 |
0 |
|
, |
||
|
|
|
0 |
0 |
0 |
2(1+v) |
0 |
0 |
|
|||
|
|
|||||||||||
|
|
|
E |
|
|
|||||||
|
|
|
|
|
0 |
0 |
0 |
0 |
2(1+v) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
2(1+v) |
|
||||||
где E – модуль Юнга, v – множитель Пуассона, который определяет сжатие в перпендикулярном направлении.
Уравнения равновесия в 3D-среде имеют следующий вид:
− ∂σx − 2 |
∂σxy |
|
− |
∂σxz = F ; |
|
|||||||||
|
|
|
||||||||||||
|
∂x |
∂y |
|
|
|
|
∂z |
x |
|
|||||
|
|
|
|
|
|
|
||||||||
|
∂σ |
xy |
|
|
|
∂σ |
y |
|
|
∂σ |
yz |
= Fy ; |
|
|
− |
|
−2 |
|
|
− |
|
(3.12) |
|||||||
|
|
|
|
|
|
|||||||||
|
∂x |
∂y |
∂z |
|
|
|||||||||
|
∂σxz −2 |
|
∂σyz |
− |
∂σz = F . |
|
||||||||
− |
|
|
||||||||||||
|
|
|
||||||||||||
|
∂x |
∂y |
∂z |
z |
|
|||||||||
|
|
|||||||||||||
|
|
|||||||||||||
где Fi – компоненты силы, действующей на тело.
В FEMLAB существуют следующие режимы решения задач теории упругости:
–Статическая задача (Static analysis).
–Задача на собственные значения (Eigenfrequency analysis).
–Переходный анализ (Transient analysis).
92
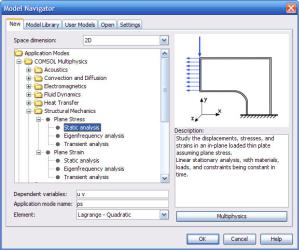
3.5.2. Прикладной режим уравнений строительной механики
Моделирование задач теории упругости в системе FEMLAB имеет некоторые особенности. Откроем прикладной режим Comsol
Multiphysics->Structural Mechanics->Plane Stress->Static Analysis
(рис. 3.33).
Рис. 3.33. Прикладные режимы строительной механики в навигаторе моделей
Создадим в открывшейся геометрии какую-либо область и вы-
зовем окно Subdomain Settings (рис. 3.34).
Поскольку уравнения системы имеют сложный вид, в окне они не показаны, в отличие от других прикладных режимов. Первая вкладка Material отвечает за свойства материала области.
E – модуль Юнга.
v – множитель Пуассона. ρ – плотность материала.
93

Рис. 3.34. Задание свойств среды в окне Subdomain Settings
Особо следует отметить поле thickness. В режиме уравнений строительной механики, любая двумерная задача будет все равно представляться как трёхмерная. Таким образом, каждая нарисованная двумерная фигура имеет некоторую толщину в трёхмерном пространстве, которая задаётся полем thickness (переменная задачи
– th). В аксиальной 2D-геометрии этого поля нет, в данном случае объёмность фигуры достигается за счёт вращения области оси Z.
3.5.3. Закрепления
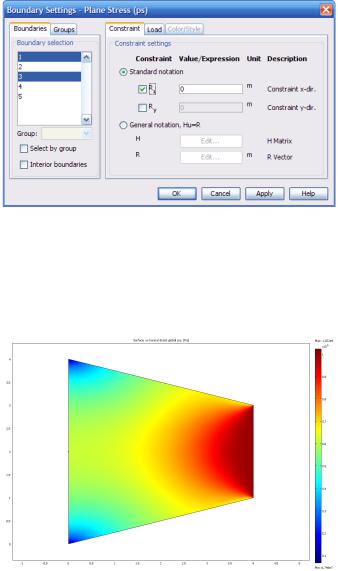
Следующая особенностью данного прикладного режима – это закрепление области (Constraints). Любая часть твёрдой конструкции может быть жёстко закреплена. Поэтому вкладка Constraint доступна для всех видов условий, и во всех случаях она выглядит одинаково. Можно закреплять отдельные точки, рёбра, поверхности, а также саму область в 3D-геометрии, или точки, границы и саму область в 2D-геометрии (рис. 3.35).
94
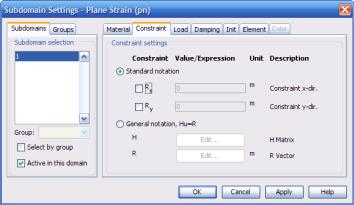
Рис. 3.35. Вкладка задания закреплений элементов конструкции
Закрепления фиксируют деформации области. Переключатель Standard notation задаёт значения деформаций вдоль главных осей
вявном виде. Закрепление вдоль каждой из осей действует, если
включён соответствующий флажок. Так, если включён флажок Rx, то закрепление будет действовать только вдоль оси Х, вдоль оси Y деформация может свободно меняться.
Переключатель General notation позволяет задать деформации
вобщем виде. В этом случае значения деформаций будут решением матричного уравнения Hu=R.
3.5.4. Нагрузки
Помимо закреплений для всех типов условий можно задать нагрузки. Нагрузки – это компоненты силы Fx, Fy, Fz в уравнении равновесия. Их можно задать во вкладках Load (рис. 3.36).
Нагрузки, воздействующие на область, могут задаваться как сила на единицу площади (переключатель Body load is defined as force/area) или как сила на единицу объёма (переключатель Body load is defined as force/volume using the thickness). Во втором слу-
чае используется значение толщины фигуры из поля thickness вкладки Material. Для граничных условий нагрузка задаётся как сила на единицу длины, или на единицу площади (с использованием толщины). Для точек нагрузка задаётся как абсолютное значе-
95
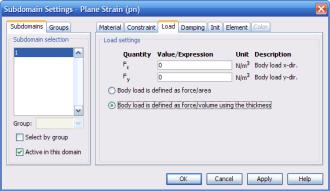
ние силы или как сила на единицу длины (с использованием толщины фигуры).
Рис. 3.36. Вкладка задания нагрузок на конструкцию
3.5.5.Пример задачи распределения напряжений
втрапециевидной мембране
Решим задачу распределения напряжений в трапециевидной мембране, одна сторона которой жёстко закреплена, а ко второй приложена нагрузка.
Выберем в навигаторе моделей размерность геометрии 2D и
режим Comsol Multiphysics->Structural Mechanics->Plane Stress- >Static Analysis. Нажмём OK, в открывшемся окне нарисуем трапецию последовательностью линий (рис. 3.37):
[(0; 0), (0; 2)]; [(0; 2), (0; 4)]; [(0; 4), (4; 3)]; [(4; 3), (4; 1)]; [(4; 1), (0; 0)].
Левое основание трапеции составлено из двух отрезков. Далее будет понятно, зачем так было сделано.
Откроем окно Physics->Subdomain Settings. На вкладке Material введём следующие значения переменных (рис. 3.38):
E: 210e9; v: 0.3;
ρ: 7850;
96
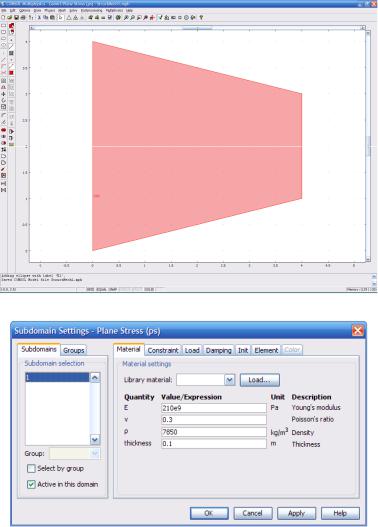
thickness: 0.1.
Рис. 3.37. Рисование геометрии мембраны
Рис. 3.38. Задание физических свойств мембраны
Остальные вкладки оставим без изменений. Перейдём к заданию граничных условий. Откроем окно Physics->Boundary Settings. В списке Boundaries выберем границы 1 и 3. Для них вклю-
97
чим флажок Rx. Значение поля Rx следует оставить равным нулю
(рис. 3.39).
Рис. 3.39. Задание закреплений на границе мембраны
Далее откроем вкладку Load и выберем границу 5. Введём в поле Fx величину 10e6.
Далее зададим точечные условия. Откроем окно Physics->Point Settings. Для точки 2 включим закрепления Rx, Ry.
Теперь можно сгенерировать сетку и запустить решение (рис. 3.40).
Рис. 3.40. Распределение напряжений σxx в мембране
98
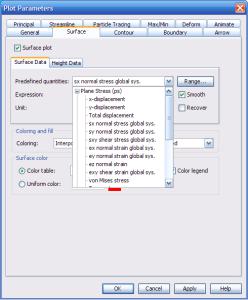
В свойствах графика (окно Plot->Plot Parameters) предлагается довольно большой выбор компонент тензоров деформаций и напряжений для построения (рис. 3.41).
Рис. 3.41. Окно свойств графика. Выбор компонент тензоров напряжений и деформаций для визуализации
Также, кроме данных компонент, можно построить свёртки тензоров, первые, вторые и третьи главные напряжения и другие величины.
3.6. Решение задачи нахождения скоростей течения льда системой FEMLAB
3.6.1. Теоретические сведения
Для дальнейшего изучения возможностей системы FEMLAB разработаем модель расчёта скоростей течения льда в горном леднике.
99
Лёд представляет собой пластическую вязкую среду, которая может быть описана с помощью уравнений гидродинамики:
∂vG |
G G |
|
= − |
p |
G |
||
|
|
+ (v, )v |
|
|
+ F; |
||
∂t |
|
|
|
ρ |
(3.13) |
||
|
∂ρ |
|
G |
|
|
|
|
|
|
|
|
|
|
||
|
∂t |
= div(ρv), |
|
|
|
|
|
|
|
|
|
|
|
|
|
где vG – скорость течения льда, ρ – плотность льда, p – давление, F
– сторонняя сила, в данном случае, это сила тяжести. Для упрощения расчётов будем использовать двумерную геометрию в задаче. Область ледника ограничена поверхностями hb снизу и hs сверху.
Лёд принимается несжимаемым веществом, поэтому |
∂ρ |
= 0 . Ско- |
|
∂t |
|
рости течения достаточно малы, поэтому в уравнении движения мы
можем пренебречь слагаемыми |
∂v |
G |
G |
|
∂t |
+ (v |
; )v . Для льда выполняет- |
||
ся реологический закон Глена: |
|
|
|
|
|
|
|
|
|
ε• ik = A(T )(σ')n−1σ' |
|
|
|
(3.14) |
ik , |
|
|
|
|
|
|
|
ik |
– тен- |
где σ – тензор напряжений, σ’ – девиатор напряжений), ε |
||||
зор скоростей деформаций, η – |
вязкость, n–показатель Глена |
|||
(обычно n=3). Закон связывает компоненты скорости течения с компонентами деформации. Величины A зависит от температуры льда, размера кристаллов и их ориентации, содержания примесей и других факторов.
Вместе с законом Глена, система уравнений течения ледника имеет следующий вид:
100
