
Красников Моделирование физических процессов с исползованием 2012
.pdf∂u +u ∂u + v ∂u −∂t ∂x ∂y
∂∂vt +u ∂∂vx + v ∂∂vy −
∂u + ∂v = 0.
∂x ∂y
u + ∂∂px = 0,
v + |
∂p |
(3.4) |
= 0, |
||
|
∂y |
|
При дискретизации области система станет дифференциальноалгебраической, поскольку третье уравнение приведёт к алгебраическому соотношению. Давление p имеет индекс 2, поскольку для нахождения производной давления по времени необходимо сначала проинтегрировать третье уравнение по времени, а затем проинтегрировать каждое из первых двух. Скорости u и v имеют индекс 0, поскольку явно заданы в первых двух уравнениях.
Переменные с индексом 0 называют дифференциальными переменными, а все остальные – алгебраическими. Задачи, приводящие при дискретизации к дифференциально-алгебраическим системам, считаются одними из наиболее сложных для решения. Следует учитывать особенности решения подобного класса задач в
FEMLAB.
Откроем вновь окно Solver Parameters и вернёмся на вкладку Time Stepping свойств решателя нестационарных задач. Если наша модель содержит дифференциально-алгебраическую систему, которая приводит к сингулярной матрице, то в панели Advanced в свойстве Singular mass matrix следует выбрать пункт Yes.
3.2. Решение задач с собственными значениями
Задача на собственные значения функции во многом аналогична нестационарной задаче. В уравнении производная по времени
∂u заменяется на слагаемое –λu. Таким образом, уравнение тепло-
∂t
проводности принимает вид:
1 |
T + λu = 0. |
(3.5) |
|
a |
|||
|
|
71
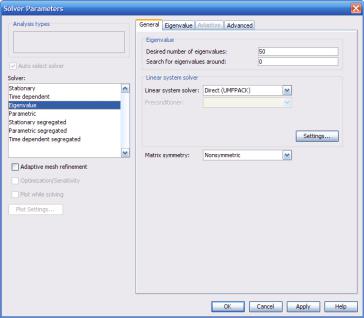
Попробуем решить задачу на собственные значения уравнения теплопроводности из предыдущего случая. В первую очередь в свойствах решения следует выбрать решатель Eigenvalue (рис. 3.15).
Рис. 3.15. Настройка свойств решателя задач на собственные значения
Поле Desired number of eigenvalues – ключевое, здесь указы-
вается количество собственных чисел λ, для которых будет считаться уравнение. Поле Search for eigenvalues around указывает величину, в окрестностях которой будут искаться собственные значения. Панель Linear System Solver отвечает за выбор линейного решателя.
Укажем число собственных значений 50, а поле Search for eigenvalues around оставим равным 0. Кроме того, следует заменить граничное условие на нижней границе на условие Дирихле u=0 (h=1, r=0), поскольку в данной задаче время не используется. Теперь можно запускать решение (рис. 3.16).
72
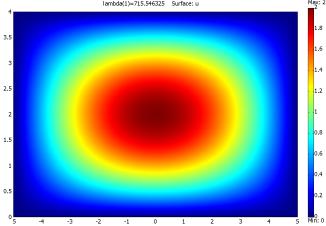
Рис. 3.16. Решение с минимальным значением λ
Это решение при самом малом значении λ, оно ничем не отличается от решения соответствующей стационарной задачи. Чтобы посмотреть решения для других собственных значений, нужно в окне Plot parameters во вкладке General выбрать необходимое собственное значение из выпадающего списка Eigenvalue. (рис. 3.17).
Следует пояснить физический смысл данных решений. Рассмотрим одномерный случай уравнения теплопроводности:
|
|
2 |
u2 = 0; |
|
∂u − α2 ∂ |
||
|
∂t |
∂x |
|
|
|
|
(3.6) |
x [0;l]; |
|||
u(0,t) |
= 0;u(l,t) = 0; |
||
|
|
|
|
|
|
= ϕ(x). |
|
u(x,0) |
|||
Как известно из курса математической физики, аналитическое решение одномерного уравнения теплопроводности с нулевыми граничными условиями будет иметь следующий вид:
∞
u(x,t) = ∑βnun (x,t);
n=1
73
Где un (x,t) – собственные функции вида
un (x,t) = sin(πln x)e−πlnα2t ;
а βn – некоторые постоянные коэффициенты, определяемые из граничных условий.
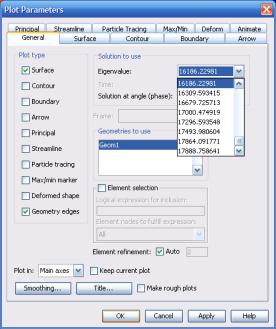
Рис. 3.17. Выбор собственного значения для построения профиля
Таким образом, исходная функция u(x,y) состоит из бесконечного ряда гармоник. Решив соответствующую задачу на собственные значения для одномерного уравнения теплопроводности, можно убедиться, что её решения будут соответствовать функциям un (x,t) при t=0. В двумерном случае работает аналогичный принцип
– можно видеть, что разные собственные значения λ соответствуют разному набору гармоник по Х и Y.
74

Рис. 3.18. Решения задачи уравнения теплопроводности при разных значениях λ
Ряд графиков собственных функций можно просмотреть одним видеороликом в виде набора слайдов. Для этого на вкладке Animate окна Plot Parameters в поле Solutions to use следует выбрать те собственные значения, решения для которых должны войти в ролик. Запустить ролик можно кнопкой Start Animation.
Рис. 3.19. Настройка видеоролика с решениями для разных собственных чисел λ
75
Панель Static / Eigenfuction Animation используется, если вы-
бран только один пункт. В этом случае ролик будет показывать только это решение. В данном случае система представляет статическое решение ui (x, y) , как изменяющееся во времени по сину-
соидальному закону (ui (x, y) cosωt ). В поле Cycle type указывается
продолжительность отображения:
Full harmonic – будет показана полная синусоида; Half harmonic – будет показана половинка синусоиды; Linear – будет показана четверть синусоиды.
В поле Number of frames указывается количество кадров в ролике. Таким образом, чем выше значение в поле, тем ролик будет более гладкий.
3.3. Решение задач с параметром
Система FEMLAB позволяет решать уравнения, в которых одна из входящих в него величин является некоторым независимым параметром, принимающим определённый набор значений. Эта возможность полезна при необходимости решить одну задачу несколько раз, но для разных значений какой-либо величины. В этом случае целесообразнее использовать специальный параметрический решатель, который способен за короткое время решить одну задачу для большого числа значений параметра.
Загрузим снова модель с уравнением теплопроводности на прямоугольной области. Чтобы решать задачу с параметрами, следует выбрать параметрический решатель. Делается это выбором пункта Parametric linear в окне Solver Parameters. Решатель Parametric nonlinear работает аналогично линейному, но для нелинейных задач. Перед нами появится форма, представленная на рис. 3.20.
В поле Name of parameter указывается имя используемого параметра, а в поле List of Number values массив, содержащий значения параметра. Задание массива производится в соответствии с правилами задания массивов и векторов в Matlab.
1 2 5 10 20 50 100 150 – набор чисел, разделённый пробелом.
76
range(0,0.1,10) – вектор с равномерно распределёнными значениями от 0 до 10 с интервалом 0.1. Значениями будут 0.1,
0.2, 0.3 и т.д.
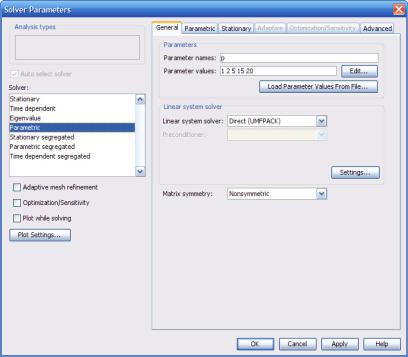
Рис. 3.20. Настройка свойств параметрического решателя
Кнопкой Edit… можно более детально задать массив значений параметра. Подробнее про указание массива написано в п. 3.1.2. Помимо этого, массив значений можно загрузить из файла нажати-
ем кнопки Load Parameter Values From File…
После того, как указано имя параметра и хотя бы одного его значения, этот параметр можно использовать в любых местах задачи: регулярных выражениях, коэффициентах уравнения, граничных и точечных условиях, в выражении для графиков. Введём имя параметра и набор значений в соответствии с рис. 3.20. Значение поля f в окне задания коэффициентов уравнения Subdomain Settings укажем равным p. Запустив решатель, получим решения для 5 раз-
77

личных значений. Просмотреть разные решения можно выбирая различные значения параметра в поле Parameter value в окне Plot Parameters (рис. 3.21).
Рис. 3.21. Выбор значения параметра для построения профиля
Также набор решений можно посмотреть в виде клипа (вкладка Animate). Принципы работы с клипом описаны в п. 3.2.
3.4. Решение уравнений акустики
3.4.1. Общие сведения
Акустика – наука о распространении звука. Звук, воспринимаемый ухом, это малые колебания в плотности и давлении среды. Эти колебания распространяются в виде продольных волн. Существует пять основных задач акустики.
Излучение звука. Вибрирующая область излучает в окружающее пространство звуковые волны. Для моделирования неограни-
78
ченной области необходимо задавать сильно удалённое граничное условие.
Рассеяние звука. Падающая на некую поверхность звуковая волна рассеивается и создаёт рассеянную волну.
Распределение звукового поля в замкнутой области. Наибо-
лее распространённая задача, которая используется для организации концертных залов.
Взаимодействие звуковой волны с эластичными поверхно-
стями. Если излучающая или рассеивающая поверхность сделана из эластичного материала, то следует учитывать взаимодействие между средой и этой поверхностью.
Переход волны. Решаются задачи распространения волны в среде с другими акустическими свойствами.
3.4.2. Математическая постановка задачи
Постановка задачи основана на волновом уравнении:
1 |
|
∂ |
2 |
p2 |
|
1 |
|
|
|
+ − |
p + qG = 0 , |
(3.7) |
|||||
|
|
|||||||
ρ0c |
2 |
|
|
ρ0 |
||||
|
∂ρ |
|
|
|
||||
где ρ0, p0 – стационарные значения плотности и давления, вокруг которых происходят колебания, q – некий дипольный источник, с – скорость звука в среде.
Рассмотрим частный случай, когда распространение звука, это гармоническая волна. В этом случае давление изменяется со временем по закону:
p= p0eiωt .
Втаком случае, уравнение (3.7) преобразуется в уравнение Гельмгольца:
|
|
1 |
p +qG |
|
|
ω |
2 |
p20 |
= 0 . |
(3.8) |
|
− |
|
− |
|
||||||
ρ0 |
|
|
||||||||
|
|
|
|
|
ρ0c |
|
|
|||
3.4.3. Прикладной режим уравнений акустики
Прикладной режим уравнений акустики включает в себя два подрежима:
– Временной гармонический анализ;
79

– Задачу на собственные значения.
В первом режиме решается уравнение Гельмгольца для давления. Во втором режиме решается задача на собственные значения
|
|
1 |
|
|
λp |
|
|
|
− |
p |
− |
= 0 |
|
||
ρ0 |
2 |
(3.9) |
|||||
|
|
|
|
ρ0c |
, |
где собственное значение λ связано с собственной частотой f:
λ = (2π f )2 .
Рис. 3.22. Форма задания коэффициентов системы уравнений акустики
Форма для задания уравнения выглядит следующим образом
(рис. 3.22).
ρ0 – плотность среды (в системе обозначается, как rho0). По умолчанию 1,25 кг/м3;
cs – скорость звука в среде, по умолчанию 343 м/с; Q – монопольный источник;
q – дипольный источник (компоненты обозначаются как qx,
qy, qz).
80
