
Обыкновенные дифференциальные уравнения с приложениями к задачам механики, физики, термодинамики и экологии. Ряжских В.И., Бырдин А.П
.pdf
В. И. Ряжских, А. П. Бырдин, А. А. Сидоренко
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С ПРИЛОЖЕНИЯМИ К ЗАДАЧАМ МЕХАНИКИ,
ФИЗИКИ, ТЕРМОДИНАМИКИ И ЭКОЛОГИИ
Учебное пособие
divFdV FndS
V S
Воронеж 2019
МИНИСТЕРСТВО НАУКИ И ВЫCШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
В. И. Ряжских, А. П. Бырдин, А. А. Сидоренко
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С ПРИЛОЖЕНИЯМИ К ЗАДАЧАМ МЕХАНИКИ,
ФИЗИКИ, ТЕРМОДИНАМИКИ И ЭКОЛОГИИ
Учебное пособие
Воронеж 2019
УДК 517.9(075.8) ББК 22.161(я7)
Р989
Р е ц е н з е н т ы:
кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. В. А. Костин); канд. физ.-мат. наук, доцент И. В. Колесникова
Ряжских, В. И.
Обыкновенные дифференциальные уравнения с приложениями Р989 к задачам механики, физики, термодинамики и экологии: учебное
пособие / В. И. Ряжских, А. П. Бырдин, А. А. Сидоренко; ФГБОУ ВО «Воронежский государственный технический университет». – Воронеж: Изд-во ВГТУ, 2019. – 181 с.
ISBN 978-5-7731-0779-8
В учебном пособии излагается теория дифференциальных уравнений с приложениями к задачам механики, физики, термодинамики и экологии. Теоретический материал иллюстрируется большим количеством примеров. Имеются задачи для самостоятельного решения.
Издание предназначено для студентов по направлению подготовки бакалавров 21.03.01 «Нефтегазовое дело» (профиль «Эксплуатация и обслуживание объектов транспорта и хранения нефти, газа и продуктов переработки»), 13.03.01 «Теплоэнергетика и теплотехника» (профиль «Промышленная теплоэнергетика»), специальностей 24.05.07 «Самолето- и вертолетостроение», 24.05.02 «Проектирование авиационных и ракетных двигателей» очной и заочной форм обучения.
Ил. 14. Библиогр.: 12 назв.
УДК 517.9(075.8) ББК 22.161(я7)
Печатается по решению учебно-методического совета Воронежского государственного технического университета
ISBN 978-5-7731-0779-8 |
© Ряжских В. И., Бырдин А. П., |
|
Сидоренко А. А., 2019 |
|
© ФГБОУ ВО «Воронежский |
|
государственный технический |
|
университет», 2019 |
2

ВВЕДЕНИЕ
Для того чтобы сделать ум проницательным, необходимо упражнять его в исследовании вещей, уже найденных другими…
Рене Декарт (1596-1650 г.) “Правила для руководства ума”, правило X.
Дифференциальные уравнения являются важнейшим разделом курса высшей математики, преподаваемым будущим инженерам, обучаемых в технических вузах. Это положение данного раздела курса особенно усиливается чрезвычайно большой ролью, которую дифференциальные уравнения играют в математике и ее многочисленных физических и технических приложениях. В этой связи в курсе дифференциальных уравнений наряду с изучением теории и методов решения должно уделяться достаточное внимание приложениям, чтобы показать эффективность их применения. Каждая отрасль естествознания и техники, разрабатывая математические модели процессов, занимается решением своих дифференциальных уравнений, связанных с собственной проблематикой, в общем курсе дифференциальных уравнений следует заниматься не только решением готовых уравнений, но и уделять время составлению уравнений по условиям конкретных задач.
Дифференциальные уравнения, как и дифференциальное исчисление, возникли в XVII веке. Исаак Ньютон рассматривал дифференциальные уравнения в работе 1671 г. и решения уравнений получал с помощью интегрирования и разложения в ряды. В этой работе, в частности, Ньютон рассмотрел решение дифференциальных уравнений вида
y 1 3x x2 (1 x)y, |
y(0) 0. |
Ньютон исследовал решение этого уравнения с помощью бесконечного ряда. В качестве первого члена ряда выбиралось начальное значение при x 0:
y 0 .
Подставляя его в правую часть уравнения, получим y 1, что при интегрировании дает y x .
Продолжая этот процесс, Ньютон получил приближенное решение
y x x2 x3 x4 x5 x6 .
3 6 30 45
Можно показать, что полученное приближенное решение близко к точному только при малых значениях x.
Свое изобретение дифференциальных уравнений Ньютон считал настолько важным, что зашифровал в виде ипограммы, смысл которой ученые передают так: “Законы природы выражаются дифференциальными уравнениями”.
3
Второй изобретатель дифференциального исчисления Готфрид Вильгельм Лейбниц (1636 – 1716) открыл дифференциальные уравнения около 1676 г. Центральным пунктом размышлений Лейбница являлся поиск “универсального метода”, который сводил умозаключения к вычислениям. Погружаясь в размышления, Лейбниц перемещал по столу с помощью цепочки свои карманные часы. Это привело его к задаче (1693 г.), называемой “обратная задача о касательной”: найти кривую y(x) по заданной постоянной длине касательной “a”. Это привело Лейбница к получению дифференциального уравнения первого порядка:
y |
|
y |
||
|
|
|
. |
|
|
|
|
||
|
||||
|
|
a2 x2 |
||
Из огромного числа работ XVIII века по дифференциальным уравнениям выделяются работы Леонарда Эйлера (1707-1783) и Жозефа Луи Лагранжа (1736-1813). Решения линейного однородного и неоднородного уравнений n го порядка с постоянными коэффициентами было найдено Эйлером в 1739г. Метод вариации постоянных разработан Лагранжем в 1775 г. Однако Эйлер использовал такой метод в различных задачах, начиная с 1739 г. В работах Эйлера и Лагранжа на основе линейных дифференциальных уравнений была развита теория малых колебаний. Вслед за Ньютоном, Лагранжем и Лапласом (Пьер Симон Лаплас, 1749-1827), а позже Гауссом (Карл Фридрих Гаусс, 17491827), были развиты методы возмущений, которые применялись для вычисления возмущений планеты.
На протяжении XVIII века теория дифференциальных уравнений позволила сделать решающие сдвиги в земной и небесной механике, теории приливов, в метеорологии и в других областях науки.
Новый этап развития теории дифференциальных уравнений начинался с работ Анри Пуанкаре (1857-1912). Созданная им “качественная теория дифференциальных уравнений” вместе с теорией функций комплексных переменных привела к основанию совершенно новых направлений развития математики.
Значительный вклад в развитие теории дифференциальных уравнений внесли отечественные математики: А.Н. Ляпунов (1857-1918) – развитие теории устойчивости движения, А.А. Андронов (1901-1952) – теория ветвления решений, Л.С. Понтрягин – теория структурной устойчивости, Н.М. Крылов (1879-1955) и Н.Н. Боголюбов – теория усреднения.
Однако успехи физики XX века показали ограниченность механического детерменизма и недостаточность классической математики для описания явлений в микромире. Создаваемая уже в конце XIX и XX веках новая математика позволила объяснять экспериментальные результаты в физике микромира на основе новых абстрактных математических теорий, в том числе на базе современной теории дифференциальных уравнений.
4

1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА. ОСНОВНЫЕ ПОНЯТИЯ
1.1. Понятие обыкновенного дифференциального уравнения, общего и частного решений. Геометрический смысл решения
Многочисленные вопросы науки и техники требуют не только отыскания скорости изменения величин по заданной физической или технической характеристике процесса (т.е. отыскания производных), но и решения обратной задачи – восстановление функции по ее заданной производной. Если задано,
например, ускорение движения a a(t), |
то восстановить скорость движения |
v v(t) или уравнения движения s s(t) |
можно с помощью интегрирования. |
Именно, поскольку a dv , где a(t) - заданная функция времени, то получаем dt
уравнение |
|
||
|
dv(t) |
a(t), |
(1.1) |
|
|
||
|
dt |
|
|
из которого определяется скорость движения с точностью до постоянной |
|
||
v(t) a(t)dt C, |
(1.2) |
C - произвольная константа. Неопределенный интеграл в решении (1.2) можно |
|
заменить определенным интегралом с переменным верхним пределом. |
|
t |
|
v(t) a(t)dt C, |
|
t0 |
|
где t0 и t - принадлежат области, в которой задана функция a(t). |
f (x), |
Таким образом, задача отыскания первообразной для функции |
|
заданной в интервале x (a,b), приводит к простейшему дифференциальному уравнению
y |
f (x), x (a,b). |
(1.3) |
Если f (x) непрерывная |
на этом интервале функция, |
то решение |
уравнения, как известно из курса математического анализа, дается формулой x
y f (x)dx C,
|
|
x0 |
|
|
|
где x0,x (a,b), C - произвольная постоянная. |
|
|
|||
Уравнение |
(1.3) |
представляет |
собой |
наипростейший |
тип |
дифференциальных уравнений. |
|
|
|
||
Для потребностей |
самой математики, а также ее приложений в |
||||
естественнонаучных |
и технических дисциплинах, |
приходится определять |
|||
|
|
5 |
|
|
|
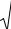
функцию y y(x) из более сложных соотношений, связывающих значения независимой переменной x со значениями как самой неизвестной функции y,
так и ее производных |
|
|
|
|
|
|
|||
y |
,y ,...: |
|
|
|
|
||||
|
|
|
|
|
F |
|
(n) |
) 0, |
(1.4) |
|
|
|
|
|
(x, y, y ,...,y |
|
|||
|
(n) |
) |
- |
|
заданная функция |
(n 1) |
- переменных. Такого рода |
||
где F(x, y, y ,...,y |
|
|
|||||||
соотношения называются обыкновенными дифференциальными уравнениями.
Термин “обыкновенное” означает, что входящая в уравнение неизвестная
функция зависит только от одной независимой переменной x. |
|
|
||
Обыкновенным дифференциальным |
уравнением |
1-го |
порядка |
|
называется соотношение, связывающее независимую |
переменную x, |
|||
неизвестную функцию этой переменной |
y(x) |
и ее производную 1-го порядка |
||
y (x). |
|
|
|
|
Общий вид уравнения таков: |
|
|
|
|
F(x, y, y ) 0, |
|
(1.5) |
||
|
|
|
|
|
где F(x, y, y ) - заданная функция. |
|
|
|
|
Решением дифференциального |
уравнения (1.5) |
назовем |
всякую |
|
дифференцируемую функцию y (x), удовлетворяющую |
этому уравнению, |
|||
т.е. обращающую его в тождество по крайне мере в некотором промежутке изменения x:
|
|
|
|
|
F(x, (x), (x)) 0. |
|
|
Например, |
одним из решений уравнения y |
1 y2 |
является функция |
||||
y sin x при x |
|
|
|
|
|
||
|
|
, |
|
. |
|
|
|
2 |
|
|
|
||||
|
|
|
2 |
|
|
||
Если уравнение (1.5) можно разрешить относительно производной, то оно
примет вид |
|
y f (x, y). |
|
(1.6) |
||
|
|
|
||||
Заменив производную отношением дифференциалов, уравнение (1.6) |
||||||
можно записать в форме |
|
dy |
|
|
|
|
|
|
f (x, y). |
|
(1.7) |
||
|
|
|
|
|||
|
|
dx |
|
|
|
|
Частным случаем |
уравнения |
(1.6) |
является |
простейшее |
||
дифференциальное уравнение y f (x). |
|
|
|
|||
Общим решением уравнения (1.6) или (1.7) называется дифференциру- |
||||||
емая по x функция |
y (x,C), |
|
(1.8) |
|||
|
|
|||||
зависящая от числового параметра C (“произвольной постоянной”), если она является решением дифференциального уравнения при любых допустимых значениях этого параметра.
6

Решение, полученное из общего решения (1.8) при конкретном значении параметра C, называется частным решением дифференциального уравнения.
Соотношение вида
Ф(x, y,C) 0, |
(1.9) |
определяющее общее решение как неявную функцию x и C, называется общим интегралом уравнения (1.5) или (1.6).
Частным интегралом дифференциального уравнения (1.5) или (1.6) называется соотношение вида (1.8) при фиксированном значении параметра
C.
Если рассматривать |
x и |
y как прямоугольные координаты точки на |
|||
плоскости, |
то решению |
y (x,C) |
уравнения (1.7) или (1.5) |
при |
|
фиксированном значении постоянной C будет соответствовать некоторая |
|||||
кривая на |
плоскости XOY , |
которая |
называется интегральной |
кривой |
|
дифференциального уравнения (1.7) или (1.5). Придавая произвольной постоянной C разрешенные значения, получим семейство (бесконечное множество) интегральных кривых, каждой из которых соответствует определенное значение постоянной C.
Например, дифференциальное уравнение |
|
, как легко проверить, |
|
y x y 0 |
|||
имеет общее решение y Cx, |
C . |
Интегральными кривыми этого |
|
уравнения являются прямые, проходящие через начало координат. Точка (0,0) является особой точкой дифференциального уравнения. В этой точке уравнение не устанавливает никакого соотношения между x, y и y .
Дифференциальное уравнение dy f (x, y) устанавливает зависимость dx
между координатами точки, через которую проходит интегральная кривая, и
угловым коэффициентом касательной dy к графику этой кривой в той же dx
точке. Зная x и y можно вычислить f (x, y). Следовательно, можно вычислить
dy . Сопоставляя каждой точке области, в которой определено dx
дифференциальное уравнение, вектор, направленный по касательной к графику решения, мы тем самым определяем поле направлений. Интегральные кривые – это линии, имеющие в каждой своей точке направление, определяемое дифференциальным уравнением (направление поля). Схематически поле направлений, задаваемое некоторым уравнением, показано на рис. 1.
С этой точки зрения решение дифференциального уравнения состоит в нахождении кривой на заданному в каждой точке направлению. Как видим из формулы (1.8), таких кривых на плоскости – семейство, получаемое при изменении параметра C.
7
Чтобы выделить определенную кривую из этого семейства, необходимо потребовать, чтобы линия проходила через некоторую заданную точку
(x0, y0).
Рис. 1. Поле направлений, задаваемое дифференциальным уравнением
Пример. Вернемся к уже рассмотренному выше дифференциальному
уравнению, записав |
его в виде |
|
dy |
|
y |
. |
Построим поле |
направлений, |
|
|
|
||||||
|
|
|
dx x |
точке, отличной от точки (0,0), |
||||
определяемое этим уравнением. В каждой |
||||||||
угловой коэффициент |
касательной |
к некоторой интегральной |
кривой равен |
|||||
отношению y . То есть угловой коэффициент касательной совпадает с угловым x
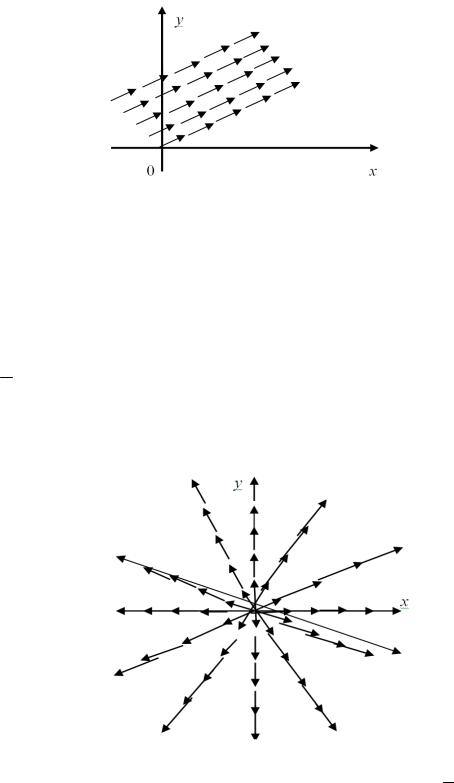
коэффициентом прямой, направленной из начала координат в ту же точку (x, y)
. На рис. 2 показано поле направлений, задаваемое этим дифференциальным уравнением.
Рис. 2. Поле направлений, определяемое уравнением y y x
8

1.2. Задача Коши для дифференциального уравнения первого порядка. Теорема существования и единственности решения задачи Коши
1. Одной из важнейших задач в теории дифференциальных уравнений и в практических приложениях теории, является так называемая задача Коши. Для уравнения (1.7)
dy f (x, y) dx
задача Коши ставится следующим образом. |
|
|
Задачей Коши (или начальной задачей) для дифференциального |
||
уравнения 1–го порядка называется задача нахождения решения |
y (x) |
|
этого уравнения, удовлетворяющего начальному условию |
|
|
y f (x, y), |
y(x0) y0, |
(1.10) |
где x0 и y0 - заданные числа.
Геометрический смысл задачи Коши заключается в том, что ищется
интегральная кривая |
дифференциального |
уравнения, проходящая через |
заданную точку плоскости M0(x0, y0). |
|
|
Например, функция y 2ex является |
частным решением уравнения |
|
y y при начальном условии y(0) 2. |
|
|
Из курса высшей математики, изучаемого в 1-ом семестре, нам известно, что в алгебре большую роль играют теоремы о числе решений алгебраических уравнений. Так, в случае линейных систем уравнений, определитель которых не равен нулю, система имеет единственное решение. Известна также основная теоремы алгебры, утверждающая что многочлен n-й степени всегда имеет ровно n корней на множестве комплексных чисел (считая корни с их кратностями). В теории дифференциальных уравнений также важнейшим является вопрос о том, насколько много решений имеет дифференциальное уравнение. Выше мы убедились, что дифференциальное уравнение имеет бесконечное множество решений. Поэтому ставится вопрос не о числе решений, а о том, как можно описать совокупность всех решений данного уравнения, как можно выделить интересующее нас решение и единственно ли решение, описываемое интегральной кривой, проходящей через точку (x0, y0) области.
Будем говорить, что задача Коши с начальными условиями (1.10) имеет
единственное решение, |
если существует такое число h 0, что в интервале |
|||||
|
x x0 |
|
h определено |
решение y (x) |
такое, что (x0) y0 |
и не |
|
|
|||||
существует решения, определенное в этом интервале и не совпадающее с
решением y (x) хотя бы в одной точке интервала |
x x0 |
h, отличной от |
точки x x0 (рис. 3). |
|
|
9
