Учебное пособие 800446

Построим общий интеграл однородного уравнения, записанного в симметрической форме. Сделаем замену искомой функции yпо формуле (2.21). Будем иметь

P(x,ux)dx Q(x,ux)(udx xdu) 0.

Поскольку

Уравнение (2.23) является дифференциальным уравнением с разделяющимися переменными. Разделяя переменные, получаем:

u u0 , где u0 - корень уравнения (2.26). Подставляя эти значения в формулу (2.21) найдем, что

являются решениями однородного уравнения, соответствующие интегральные кривые – полупрямые, примыкающие к началу координат. Эти решения могут входить в совокупность, определяемую общим интегралом уравнения, но могут быть и особыми решениями. Особыми решениями могут быть также полуоси оси OY : x 0 (y 0). Других особых решений это уравнение иметь не может.

Пример. Найти решения дифференциального уравнения

Решение. Это уравнение является однородным, т.к. коэффициентами при dx и dy являются функции одной степени однородности:

Введем замену y xu. Имеем

(x xucosu)dx xcosu(xdu udx) 0, или

dx cosudu 0. x

Интегрируя, получим: ln x sinu C. Таким образом, общий интеграл

уравнения имеет вид:

ln x sin y C. x

4. Рассмотрим геометрическое свойство интегральных кривых однородного уравнения.

Поле направлений, определяемое однородным дифференциальным уравнением 1-го порядка, а следовательно, и интегральные кривые этого уравнения обладают одним интересным свойством. Запишем однородное уравнение в виде

y , y x

и отметим, что функция (yx) сохраняет постоянное значение во всех точках любой полупрямой y kx (x 0), выходящей из начала координат, если, конечно, функция (k) существует при данном значении k . Поэтому все такие лучи являются изоклинами уравнения (2.13).

Выберем какую-нибудь интегральную кривую, не совпадающую с такими лучами. Если увеличить или уменьшить радиусы-векторы во всех точках интегральной кривой в одно и то же число раз, то получим кривую, у которой направление касательных во всех точках будет таким же, что и в соответствующих точках взятой первоначально интегральной кривой. Поэтому

22

полученные таким образом линии будут также являться интегральными кривыми уравнения.

Указанное преобразование радиусов-векторов называется

преобразованием подобия с центром подобия в начале координат. Оно означает замену текущих координат (x, y) линии текущими координатами

Таким образом, однородное дифференциальное уравнение 1-го порядка обладает следующим свойством: всякая кривая, полученная из интегральной кривой однородного уравнения преобразованием подобия с центром подобия в начале координат, тоже является интегральной кривой.

Верно и обратное утверждение: все интегральные кривые, входящие в общий интеграл

и не являющиеся лучами, выходящими из начала координат, могут быть получены при помощи преобразования подобия (2.29) из одной такой интегральной кривой.

Из приведенного свойства интегральных кривых однородного уравнения следует:

1) если интегральная кривая, отличная от луча, выходящего из точки (0,0) и, следовательно, заключенная на некотором интервале изменения x между двумя полупрямыми y uk x (k 1,2), примыкает к точке (0,0), то и все интегральные кривые, заключенные между этими лучами, примыкают к точке

(0,0);

2)если некоторая линия является интегральной кривой, то и симметричная относительно (0,0) линия является интегральной кривой;

3)если одна из интегральных кривых замкнута, то и все интегральные кривые замкнуты.

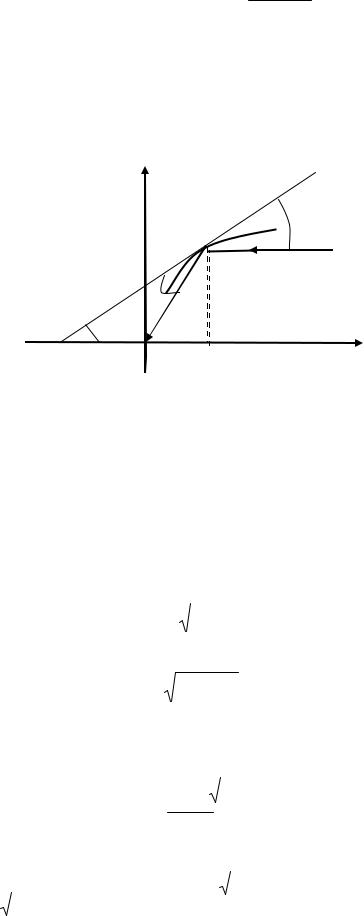
5. Рассмотрим физическую задачу, приводящую к однородному дифференциальному уравнению: найти форму зеркала, собирающего параллельные лучи в одну точку.

Выберем за ось OX прямую, параллельную лучам, за начало координат – точку пересечения всех лучей после отражения и проведем сечение поверхности зеркала плоскостью XOY . На этой плоскости будем искать кривую, обладающую указанным свойством (рис. 5).

Из геометрической оптики известно, что для идеальной зеркальной поверхности (что мы и предполагаем) углы падения и отражения равны: .

Поэтому треугольник ОТМ равнобедренный, следовательно TO OM . Если

23

точка M имеет координаты x, y, то OM 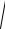x2 y2 . Координата точки T

находится из уравнения касательной

Y y y (X x),

где X,Y - текущие координаты. Полагая Y 0, X OT , получим:

TO OM , получаем дифференциальное уравнение – математическую модель задачи:

Запишем это уравнение в симметрической форме:

ydu 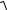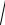u2 1dy 0.

Разделяем переменные и интегрируем. Получим:

24

Для того чтобы разрешить последнее равенство относительно u , воспользуемся элементарным приемом:

Обозначив 1 p, получим окончательно уравнение линии:

C

Таким образом, решением уравнения (2.30) служит парабола (2.33), ось симметрии которой – ось OX , а фокус лежит в начале координат. Ось искомой параболы параллельна пучку световых лучей, а фокус параболы лежит в оптическом фокусе.

Вращая эту параболу вокруг оси OX , найдем искомую зеркальную поверхность – параболоид вращения.

Очевидно, что если источник света поместить в фокусе параболы, то световые лучи после отражения пойдут параллельным пучком.

Выполним линейную замену обеих переменных

Тогда уравнение (2.34) примет вид:

Чтобы преобразовать уравнение (2.38) в однородное потребуем, чтобы свободные члены в числителе и знаменателе аргумента функции, стоящей в правой части уравнения, обращались в нуль:

a2 b2 c2 0.

Неоднородная система линейных уравнений (2.39), при условии (2.36), однозначно определяет неизвестные параметры , . Таким образом, в новых переменных X,Y получаем однородное дифференциальное уравнение 1-го порядка:

формулам (2.37), получим общий интеграл уравнения (2.34).

4. Остановимся теперь на случае, когда условие (2.36) не выполняется. Если определитель 0, элементы его строк пропорциональны:

a1 b1 k, a2 b2

поэтому a1 ka2, b1 kb2. Применяя подстановку a1x b1y z, получаем:

Таким образом, приходим к уравнению с разделяющимися переменными:

5. Имеется еще один тип дифференциального уравнения 1-го порядка, приводимое к уравнению с разделяющимися переменными – обобщенное однородное уравнение. Это уравнение вида

P(x, y)dx Q(x, y)dy 0,

где коэффициентные функции удовлетворяют условиям:

P(tx,tk y) tmP(x, y),

k m k 1

Q(tx,t y) t Q(x, y).

27

Не останавливаясь на методе интегрирования таких уравнений, отсылаем читателей к пособию (А.М. Самойленко [7]).

2.4.Линейное уравнение

1.Введем понятие линейного дифференциального уравнения 1-го порядка.

Уравнение вида

y в первой степени. Если разрешить это уравнение относительно производной, то получим уравнение

y p(x)y q(x).

Полученное уравнение является уравнением вида (2.1), в котором функция f (x, y) линейна по y, с коэффициентами, вообще говоря, зависящими от x. В частном случае p и q могут быть постоянными величинами.

28

Всюду далее будем предполагать, что функции p(x) и q(x) непрерывны

и называется однородным. Его левая часть является однородной линейной

непрерывны в интервале (a,b), причем p0(x) не обращается в нуль при всех x (a,b), то уравнение (2.43), делением обеих частей на p0(x), приводится к виду (2.41).

2. Из сформулированной в п. 1 теоремы Пикара о достаточном условии существования и единственности решения задачи Коши, вытекает, что в

предположении непрерывности функций p(x) и q(x) уравнение (2.41) имеет единственное решение y y(x), удовлетворяющее начальному условию y y0 при x x0 , где в качестве x0 можно брать любое число из интервала (a,b), а y0 можно выбирать произвольно.

Это означает, что через любую точку M0(x0,y0) полосы a x b, y ,

проходит одна и только одна интегральная кривая уравнения (2.41).

Отсюда следует, что вся указанная полоса на плоскости XOY заполнена непересекающимися гладкими интегральными кривыми линейного уравнения. При этом каждая интегральная кривая определена во всем интервале (a,b) и представляет собой график частного решения (рис. 6). Интегральные кривые

однородного уравнения (2.42) не могут пересекать ось OX . Действительно,

поскольку y 0 (a x b) является решением уравнения (2.42), то пересечение интегральной кривой оси OX означало бы нарушение единственности решения уравнения (через точку пересечения проходили бы две интегральные кривые).

3. Рассмотрим построения общего решения однородного уравнения,

соответствующего неоднородному линейному уравнению. Записав уравнение (2.42) в симметрическом виде

dy p(x)ydx 0,

получаем уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, имеем:

29