
Учебное пособие 800446
.pdf
|
|
|
|
(1) |
|
(2) |
|
(1) |
0 |
|
|
|
|
|
|
1 |
1 |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
(2) |
|
|
(2) |
0 |
|
|
|
|
|
|
1 |
2 |
|
||||
|
|
|
|
(1) |
|
(1) |
|
|
(2) |
0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
(2) |
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
0. |
|
||
|
|
|
|
|
1 |
2 |
|
||||
|
Следовательно, из искомых постоянных две произвольны, |
например, |
|||||||||
2(2) |
C2 |
1(1) |
C1, поэтому из этой системы для остальных 1(2), |
2(1) будет |
|||||||
2(1) C1 C2. Отсюда общее решение исходной системы будет 1(2) C2. y C1ex C2xex
z( C1 C2)ex C2xex.
3.Если среди корней характеристического уравнения (5.63) есть
комплексное |
спряженные |
пары |
|
m m i m, |
m 1 m i m , то |
этим |
||||||||||||||||||
корням будут соответствовать частные решения |
|
|
||||||||||||||||||||||
|
|
m(i) |
|
|
ym(1) m(1) |
e( m i m), |
ym(2) m(2) e( m i m), |
|
||||||||||||||||
причем |
определяются |
из |
|
|
систем |
(5.63). |
Можно показать, |
что |
||||||||||||||||
действительные и мнимые части |
также являются решениями системы (5.57). |
|||||||||||||||||||||||
Таким образом, можно записать два частных решения: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
y |
m(1) |
|
e m (m1)cos mx (m2)sin mx |
|
||||||||||||||
|
|
|
|
|
|
|
|
m(2) |
e m |
|
|
(m2)sin mx , |
|
|||||||||||
|
|
|
|
|
|
|
y |
m cos mx |
|
|||||||||||||||
где m(1), |
m(2), |
|
|
(m1), |
|
|
m(2) |
- действительные коэффициенты, связанные с |
||||||||||||||||
|
|
|||||||||||||||||||||||
m(1), |
m(2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, можно составить фундаментальную систему решений |
|||||||||||||||||||||||
только из действительных решений. |
|
|
|
|
|
|
|
|||||||||||||||||
|
Пример 3. |
|
|
Дана |
система |
|
дифференциальных уравнений |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dy1 |
|
|
7y |
y |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy2 |
|
2y1 |
5y2. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
Найдем ее общее решение.
Решение. Характеристическое уравнение для этой системы имеет вид
|
7 |
1 |
0 |
или |
|
2 |
12 |
|
37 |
|
0, |
|
2 |
5 |
|||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
корни этого уравнения 1 6 i, |
2 6 i. |
|
|
|
|
|
|
||||
Подставляя эти корни в (5.63), получим |
|
|
|
|
|
|
|||||
|
|
|
|
150 |
|
|
|
|
|
|
|
1(1) 1, 2(1) 1 i.
Соответствующее частное решение yij (x) будет
y1(1) e( 6 i)x; y2(1) (1 i)e( 6 i)x .
Для 2 6 i, получим соответственно
1(2) 1, 2(2) 1 i;
y1(2) e( 6 i)x; y2(2) (1 i)e( 6 i)x.
Поскольку из четырех получившихся функций в общее решение для1, 2 должны войти лишь два линейно независимых решения с произвольными постоянными C1, C2, преобразуем получившиеся решения следующим образом
y(1) |
e 6x (cosx isin x); |
1 |
|
y2(1) |
(1 i)e 6x(cosx isin x); или |
y(1) |
e 6x cosx ie 6x sin x; |
1 |
|
y(1) |
e 6x(cosx sin x) ie 6x(cosx sin x); |
2 |
|
для |
y1(2), y2(2) |
будет |
|
|
|
|
|
|
|
|
|||||||
y(2) |
e 6x cosx ie 6x sin x), |
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2(2) |
e 6x (cosx sin x) ie 6x (cosx sin x). |
|
|
|
|||||||||||||
Поэтому составляя общее решение из действительных и мнимых частей |
|||||||||||||||||
этих решений для yij (x).найдем |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
y |
|
C e 6x |
cosx C |
2 |
e 6x sin x. |
|
|
|
||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
2 |
C e 6x |
(cosx sin x) C |
2 |
e 6x (cosx sin x). |
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
n-го |
||
Известно, что линейное однородное дифференциальное уравнение |
|||||||||||||||||
порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dn y |
|
|
|
dn 1y |
|
|
dn 2 y |
|
dy |
|
|||||
|
|
|
an 1 |
(x) |
|
|
an 2 |
(x) |
|
|
... a1(x) |
|
a0y |
(5.65) |
|||
|
|
|
|
|
dxn 2 |
|
|||||||||||
|
|
dxn |
|
|
|
dxn 1 |
|
|
|
dx |
|
||||||
эквивалентно линейной, однородной системе
|
dy0 |
y |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
dx |
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy1 |
y2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dx |
|
|
|
|
|
|
|
|
|
|
|
(5.66) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
dyn 1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
a |
y |
0 |
a y |
... a |
n 1 |
y |
n 1 |
. |
|
|||||
|
|
||||||||||||||
|
dx |
|
|
0 |
|
1 1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
151 |
|
|
|
|
|
|
Будем считать все ak const.
Характеристическая матрица для (5.66) в этом случае будет иметь вид
1 |
0 |
|
0 |
|
|
||
|
0 |
|
1 |
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
||||||
|
a |
0 |
a |
|
a |
n 1 |
|
|
|
1 |
|
|
|
||
или
det( ) n an 1 n 1 ... a1 a0 0.
Если же вычеркнуть из матрицы первый столбец и последнюю строку,
получим определитель равный |
+I или –I. Следовательно, характеристический |
||||
многочлен, если имеет корень k |
кратности |
Sk , |
то матрица |
имеет |
|
элементарный делитель ( k)Sk . Поэтому корню |
k будут соответствовать |
||||
Sk линейно независимых решений вида |
|
|
|
|
|
(C0 C1x ... CSk 1 xSk 1)e kx. |
|
|
(5.67) |
||
Таким образом, методы |
решения |
систем |
типа |
(5.58) могут |
быть |
использованы для решения линейных дифференциальных уравнений n-го порядка, разрешенных относительно производных.
Пример 4. Найти общее решение дифференциального уравнения y 3y 3y y 0,
Обозначим y y0, |
y y0 |
y1, |
|
y |
y1 |
y2, |
y y2. |
||||||
Тогда |
|
dy0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
y , |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dx |
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dy |
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
y2 |
, |
|
|
|
|
(5.68) |
|||
|
|
|
|
|
|
|
|
||||||
|
dx |
|
|
|
|
|
|
|
|
||||
|
|
dy2 |
|
y |
0 |
3y 3y |
2 |
. |
|
||||
|
|
|
|
||||||||||
|
|
|
dx |
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Характеристическое уравнение системы (5.68) имеет вид
|
|
1 |
0 |
|
|
|
|
0 |
|
1 |
|
0, |
т.е |
|
1 |
3 |
3 |
|
|
|
2(3 ) 3 1 0 |
или |
( 1)3 0. |
||||
Поскольку корень 1 1 |
имеет кратность S 3, то, учитывая (5.67), |
|||||
получим общее решение (5.68), а следовательно, и исходного уравнения третьего порядка в виде
(C0 C1x C2x2)ex y(x).
152
Для нахождения общего решения нормальных систем дифференциальных уравнений вида
|
dy1 |
|
|
f (x, y ,..., y |
|
|
), |
|
|||
|
|
|
|
||||||||
dx |
1 |
1 |
n |
|
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
dy2 |
|
|
f2(x, y1,..., yn), |
|
|||||||
|
|
|
|
|
|||||||
|
|
|
|||||||||
dx |
|
|
|
|
|
|
|
|
|
(5.69) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dyn |
|
|
f |
n |
(x, y ,..., y |
n |
) |
|
||
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
||||
dx |
|
|
|
|
|
|
|
|
|
|
|
применяется также метод последовательного исключения неизвестных функций, то есть сведение системы (5.69) к уравнению вида (5.65). Для этого, дифференцируя первое уравнение из (5.69) по x, получим
|
d2 y |
|
|
f |
1 |
|
|
|
f |
|
|
|
|
dy |
|
|
|
|
f |
1 |
|
dy |
2 |
|
|
|
f |
1 |
|
dy |
n |
|
||||
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
... |
|
|
|
. |
||||||||||||||||
dx2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
y1 dx |
|
|
|
|
y2 dx |
|
|
yn |
dx |
|||||||||||||||||||||
Используя тот факт, |
что |
|
dyk |
|
fk , |
|
|
найдем |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
d2 y |
|
|
|
f |
1 |
|
f |
1 |
|
|
|
|
|
|
f |
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
f1 ... |
|
|
|
fn. |
|
|
|
|
(5.70) |
|||||||||
|
|
|
|
|
|
dx2 |
|
|
x |
y1 |
|
yn |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Определим xn из первого уравнения системы (5.69) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
yn g(x, y1, y2,...,yn 1, y1) |
|
|
|
|
|
|
||||||||||||||||||||||
Подставим yn |
|
|
в (5.70) |
|
и, |
таким образом, |
исключим эту неизвестную |
|||||||||||||||||||||||||||||
функцию из (5.70). Продолжая эту процедуру, можно получить уравнение n-го
порядка для одной неизвестной |
функции. |
|
|
||||||||
|
Пример 5. Найти |
общее решение |
|
|
|||||||
|
|
|
|
|
|
dy |
z, |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dx |
|
|
|
||
|
|
|
|
|
|
|
dz |
|
y. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dx |
|
|
|
||
|
Решение. |
d2 y |
|
dz |
, т.е. |
y |
y 0 . |
||||
|
dx2 |
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
Характеристическое уравнение имеет вид |
|
|
|||||||||
|
|
|
|
|
k2 1 0; |
k i, |
|||||
|
|
|
|
|
|
|
|
|
1,2 |
||
|
|
|
|
|
y(x) C eix C |
2 |
e ix |
||||
|
|
|
|
|
|
1 |
|
|
|
||
или |
y(x) C1(cosx isin x) C2(cosx isin x), тогда общее решение можно |
||||||||||
записать |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
153 |
|
|
|||
y(x) C1 cosx C2 sin x, z(x) C2 cosx C1 sin x.
5.6.Физические задачи, приводящие к уравнениям 2-го порядка
исистемам дифференциальных уравнений
1.Уравнение колебаний математического маятника.
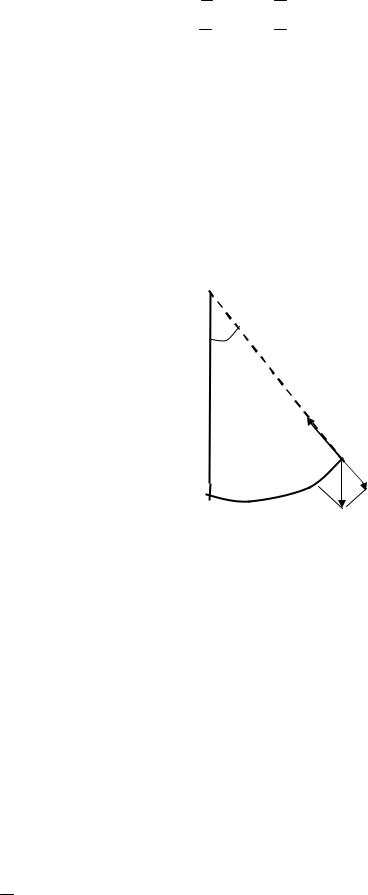
Пусть шарик массы m закреплен на конце B невесомого стержня, длина которого l. Стержень шарнирно закреплен в точке O так, что колебания маятника происходят в одной плоскости. На шарик действуют две силы: сила тяжести, направленная вертикально вниз, F mg; направленная по радиусу BO сила реакции стержня T (рис. 13).
O
l
T
 B
B
Рис. 13
Обозначим a - проекцию ускорения на направление касательной к траектории маятника. Возвращая в положение равновесия, сила – проекция силы тяжести на то же направление, равна - mgsin .
|
По второму закону Ньютона |
|
|
|
|
|||||
|
|
|
|
ma |
mgsin . |
(5.71) |
||||
|
При малых |
углах отклонения sin |
s |
|
(по теореме синусов для |
|||||
l |
||||||||||
AOB), |
где s - |
|
|
|
|
|
||||
смещение маятника, измеряемое |
длиной дуги. Поскольку |
|||||||||
a |
d2s |
, то уравнение (5.71) можно записать в виде |
|
|||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
|
dt2 |
|
|
d2s |
|
|
|
|
|
|
|
|
|
|
2s 0, |
(5.72) |
|||||
|
|
|
|
dt2 |
||||||
|
|
|
|
|
|
|
|
|||
где 2 g . Уравнение (5.72) является уравнением движения математического l
154
маятника. Решением уравнения (5.72) является функция s(t) s0 cos t, s0- начальное отклонение, начальная скорость равна нулю. Отметим, что это уравнение можно получить из уравнения Лагранжа, излагаемого в курсе теоретической механики.
Таким образом, при малых отклонениях от положения равновесия колебания маятника будут почти гармоническими с частотой , не зависящей от массы груза.
2. Уравнения упругого связанных маятников.
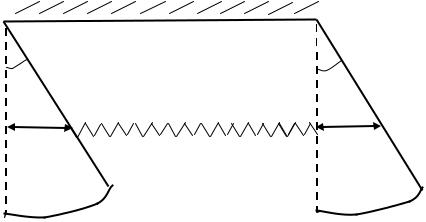
Рассмотрим связанные маятники одинаковой массы m, скрепленные пружиной жесткостью k . Пусть в некоторый момент времени стержни маятников составляют с вертикалью малые углы 1 и 2, а смещения масс от положения равновесия равны s1 и s2 (рис. 14).
O1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
O2 |
|
||
|
|
|
l |
l |
|
||||||||||||
|
|
1 |
2 |
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
x1 |
|
|
x2 |
|
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
m |
|
m |
||||||||
|
|
|
|
|
s1 |
s2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 14 |
|
|
||
В этот момент растяжение пружины равно |
|
|
|||||||||||||||
x x2 |
|
x1 lsin 2 lsin 1 l( 2 |
1) (s2 |
s1). |
|||||||||||||
Со стороны пружины на стержни подвеса маятников действуют силы |
|||||||||||||||||
упругости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 и |
F2, такие, что |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k x k (s2 s1). |
|
|||
|
|
|
|
|
F1 |
|
F2 |
|
|||||||||
Относительно осей, проходящих через точки подвеса O1 |
и O2, силы |
||||||||||||||||
создают вращательные моменты, противоположные по знаку, но одинаковые по модулю
|
M |
|
k (s |
2 |
s ) l k |
2l (s |
2 |
s ). |
|
|
|
||||||||
|
|
|
|
|
1 |
|
1 |
||
Запишем уравнение колебаний маятника (5.72) в виде |
|||||||||
|
|
|
ml |
d |
2s |
mg l . |
|
(5.73) |
|
|
|
|
dt2 |
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
155 |
|
|
|

Добавим найденные вращательные моменты с учетом соответствующих знаков в правую часть уравнения (5.73), записанного для каждого маятника. Получим следующую систему уравнений
|
|
|
|
|
d2s |
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s |
|
|
|
s ), |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
m |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
(5.74) |
|||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
d2s2 |
|
|
|
g |
s |
2 |
|
k 2 |
(s |
2 |
s ). |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Заменим систему (5.74) более удобной для решения, введя функции |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
s( ) s1 s2, |
|
|
|
|
|
s( ) s1 s2. |
|
|||||||||||||||||||||||||||||||||||||||||
Складывая и вычитая уравнения в системе (5.74) получим |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
d2s( ) |
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s( ) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
dt2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.75) |
|||||||||
|
|
|
2s( ) |
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
d |
|
|
|
|
|
|
|
|
|
|
2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s( ) 0. |
|
|||||||||||||||||||||||||||
|
|
|
dt2 |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Каждое из уравнений в (5.75) имеет вид (5.72), решение которого |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
известно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s0 |
|
|
|
|
|
|
s0, а начальные скорости |
|||||
Если начальные смещения маятников |
|
|
|
|
|
|
|
и |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
||||||||||
равны нулю, то решения уравнений (5.74) имеют вид |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
s |
|
(t) s0 cosw t, |
|
|
|
|
|
s |
|
(t) s |
0 cosw t, |
(5.76) |
|||||||||||||||||||||||||||||||||||||||||
где |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||
|
|
|
|
s0 s10 s20, |
|
|
|
|
|
|
s0 s10 s20, |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
2k 2 |
|
. |
|
|||||||||||
|
|
|
|
|
w |
|
|
|
q |
, |
|
|
|
|
|
|
w |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
m |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Возвращаясь к переменным s1 |
|
и |
|
s2, |
из (5.76) получим: |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
s0 |
|
s |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s0 |
s0 |
|
||||||||||||||||||||||
|
s (t) |
|
1 |
|
|
|
|
|
|
|
|
2 |
cosw t |
|
1 |
|
|
|
|
2 |
cosw t, |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
(5.77) |
|||||||||||||||
|
|
|
|
|
|
|
|
s0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s0 |
|
0 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
s |
2 |
(t) |
1 |
|
|
|
|
|
|
|
|
2 |
cosw t |
|
1 |
|
|
|
|
|
2 |
cosw t. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из вида решений (5.77) вытекают следующие выводы. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Если начальные |
|
|
смещения |
|
|
|
|
|
одинаковы |
|
|
|
|
|
|
s10 s20 s0, то |
маятники |
||||||||||||||||||||||||||||||||||||
колеблются с одинаковой частотой w |
|
|
|
q |
|
и постоянной амплитудой |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1(t) s2(t) s0 coswt. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
156 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

Если начальные отклонения противоположны s10 s20 s0, то колебания будут проходить с постоянной амплитудой, но с большей частотой
|
|
w |
|
q |
|
2k 2 |
, s |
(t) s |
0 |
cosw t, |
s |
2 |
(t) s |
0 |
cosw t. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2 |
|
|
l |
|
|
m |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если в начальный момент времени только один маятник смещен из |
|||||||||||||||||||||||||||||||||
положения равновесия s10 s0, |
|
s20 0, то получим |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
s (t) |
s0 |
(cosw t cosw t), |
|
s |
2 |
(t) |
s0 |
|
(cosw t cosw t). |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
1 |
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
2 |
|
1 |
|
2 |
|
|
|
||||||||
После преобразования получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
s (t) s |
0 |
cos |
w2 |
w1 |
t cos |
w2 |
w1 |
t, |
|
s |
2 |
(t) s |
0 |
|
sin |
w2 w1 |
t sin |
w2 |
w1 |
t. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|||||||||
Так как разность w2 w1 |
существенно меньше суммы частот w2 |
w1, то |
|||||||||||||||||||||||||||||||
первые члены в решениях меняются со временем гораздо медленнее, чем
cosw2 w1 t и sin w2 w1 t . Поэтому можно считать, что колебания
2 2
маятников гармонические, но амплитуды, колебаний не постоянны, а медленно изменяются.
Задачи для самостоятельного решения
Решить системы уравнений:
|
dy |
|
4y z, |
|
|
|
3x |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
y e |
(C1 |
C2x), |
||||||||
|
|
|
|
|
|||||||||||||
1. |
dx |
|
|
Ответ: |
|
|
|||||||||||
|
|
|
|
|
3x |
|
|
|
|
|
|
||||||
|
dz |
|
y 2z. |
|
z e |
(C1 |
C2 C2x). |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy |
|
y 2z, |
|
y C ex C |
|
|
e2x, |
|||||||||
|
|
|
|
|
2 |
||||||||||||
|
|
|
|
||||||||||||||
|
dx |
|
|
|
|
|
1 |
|
|
|
|
|
|||||
2. |
|
|
|
Ответ: |
z C ex 3C2 e2x. |
||||||||||||
dz |
|
3y 4z. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy |
|
2y z, |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y e |
2x |
(C1 cosx C2 sin x), |
||||||||||
|
|
|
|
||||||||||||||
3. |
dx |
|
|
Ответ: |
|
|
|||||||||||
|
|
|
|
2t |
|
|
|
|
|
|
|
||||||
|
dz |
|
y 2z. |
|
z e |
(C1 sin x C2 cosx). |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
157
dy |
y 2z, |
|
|
|
|
|
||
dx |
|
|
4. |
|
|
||||||
|
|
|
dz |
|
y z. |
|||
|
|
|
|
|
|
|
||
|
dx |
|
|
|||||
|
dy |
|
z, |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|||||
|
|
|
|
|||||
5. |
dx |
|
|
|||||
dz |
|
y. |
||||||
|
|
|
|
|
|
|||
|
dx |
|
|
|||||
|
dy |
|
y 2z. |
|||||
|
|
|
|
|||||
|
|
|
||||||
|
|
|
|
|||||
6. dx |
|
|
||||||
|
|
dz |
|
y z. |
||||
|
|
|
|
|||||
|
dx |
|
|
|||||
y C1 cosx C2 sin x, |
|
|
|
|||||
Ответ: z |
1 |
(C |
C |
2 |
)cosx (C |
C |
2 |
)sin x . |
|
||||||||
2 |
1 |
|
1 |
|
|
|||
y C1ex C2e x,
Ответ:
z C1ex C2e x.
y 2C1 cosx 2C2 sin x,
Ответ: z (C1 C2)cosx (C1 C2)sin x.
|
dy |
|
|
y z, |
y C1 C2e2x |
|
1 |
x2 x , |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
dx |
|||||||||||||||
7. |
|
|
4 |
|||||||||||||||
dz |
|
|
Ответ: |
|
2x |
|
|
1 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x y z. |
z C2e |
|
C1 |
|
4 x |
|
x 1. |
||||||
|
|
|
dx |
|
|
|
||||||||||||
|
dy |
|
2y z sin x, |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
y C1 C2x 2sinx, |
|||||||||||||
|
|
|
|
|||||||||||||||
8. |
dx |
|
|
|
Ответ: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dz |
|
4y |
2z cosx. |
|
z 2C1 |
C2(2x 1) 3sinx 2cosx. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. ПРИБЛИЖЕННЫЕ АНАЛИТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
6.1. Простейшие асимптотические методы решения дифференциальных уравнений
Во многих задачах механики колебания консервативных систем с одной степенью свободы описываются дифференциальными уравнениями вида
|
|
y0 f (y) 0, |
(6.1) |
|
где y – перемещение, f (y) – |
некоторая |
нелинейная функция от y – |
||
восстанавливающая сила, |
y– |
ускорение. |
Точками над |
буквой обозначены |
производные по времени |
t. Пусть y y0 |
определяет положение равновесия |
||
системы. Тогда f (y0) 0. Предположим, |
что функцию |
f (y) в окрестности |
||
|
|
158 |
|
|
точки y0 можно разложить в ряд Тейлора
|
|
|
f (y) k (y y |
0 |
) k |
2 |
(y y |
0 |
) |
2 k |
3 |
(y y |
0 |
)3 , |
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
где kn |
1 |
|
dn f (y0) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dyn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если считать, что восстанавливающая сила является нечетной функцией |
||||||||||||||||||
смещения от равновесия |
f ( y) f (y) (т.е. пружина ведет себя одинаково при |
|||||||||||||||||
растяжении и сжатии), |
и ограничиться в разложении функции f (y) двумя |
|||||||||||||||||
членами, то уравнение (6.1) примет вид |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x k x k |
3 |
x3 |
0, |
|
|
|
(6.2) |
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
где x y y0. Уравнение (6.2) обычно называют уравнением Дюффинга. Введем характерные масштабы задачи – линейный X и временной T , и
перейдем к безразмерным переменным |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
u |
x |
, |
|
|
t |
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
X |
|
T |
|
|
|
|
|
|||||
Используем правило дифференцирование сложной функции для перехода |
|||||||||||||||||||||
к новым переменным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d |
d d |
1 |
|
|
d |
|
d2 |
|
1 |
|
d |
|
||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
dt2 |
T2 |
d 2 |
||||||||||||
|
dt dt d |
T d |
|
|
|
|
|||||||||||||||
Тогда уравнение (6.2) преобразуется к виду
u k1T2u k3T2X 2u3 0.
Введем обозначения |
2 |
k T2 |
, |
k T2X 2 |
, где |
0 |
и - безразмерные |
|
0 |
1 |
|
3 |
|
|
параметры, - характеризует степень нелинейности системы, точка над буквой обозначает дифференцирование по .
Тогда уравнение преобразуется к виду
u 02u u3 0. |
(6.3) |
В качестве начальных условий примем
u(0) u0, |
u(0) u1. |
(6.4) |
Прямое разложение. Неравномерность разложения.
Решение уравнения Дюффинга (6.3) отыскиваем в виде ряда по степеням параметра , который считаем малым
u( , ) u |
0 |
( ) u ( ) 2u |
2 |
( ) . |
(6.5) |
|
1 |
|
|
Ограничившись в решении членом правого порядка малости
u( , )=u |
0 |
( ) u ( ) O( 2), |
(6.6) |
|
1 |
|
|
|
|
159 |
|
