
Учебное пособие 800446
.pdf
запишем преобразованное уравнение:
d(z 2) 2f (z)dz.
Интегрируя, получаем первый интеграл:
(z 2) 2 f (z)dz C1,
или
z 
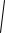 2 f (z)dz C1.
2 f (z)dz C1.
Полученное дифференциальное уравнение допускает разделение переменных. Выполнив его, найдем второй промежуточный интеграл:
|
|
|
dz |
x C2. |
|
|||
|
|
|
|
|
||||
2 f (z)dz C1 |
|
|||||||
|
|
|
|
|
|
|||
Если удалось разрешить это уравнение относительно z(x), то имеем |
||||||||
|
z (x,C1,C2), |
|
|
|
|
|||
или |
|
|
|
|
|
|
||
y(n 2) |
(x,C ,C |
2 |
). |
(3.49) |
||||
|
|
|
1 |
|
|
|
|
|
Как и в предыдущем случае (п. 3.а.1, уравнение (3.45)), полученное |
||||||||
дифференциальное уравнение (3.49) |
относится к изученному типу (3.31). |
|||||||
Таким образом, общее решение может быть получено (n 2) |
квадратурами. |
|||||||
Воспользовавшись формулой (3.30), получим общее решение уравнения (3.47):
|
|
1 |
x |
|
|
|
|
|
|
|
(x x0)n 3 |
|||
y |
|
(x s) |
n 3 |
(s,C1 |
,C2)ds C3 |
|||||||||
|
|
|
|
|
||||||||||
(n 3)! |
|
(n 3)! |
|
|||||||||||
|
|
|
x0 |
|
|
|
|
|
|
|
|
(3.50) |
||
|
|
(x x0)n 4 |
|
|
|
|
|
|
|
|
|
|
||
C4 |
|
|
Cn 1(x x0) Cn. |
|
|
|||||||||
|
|
|
|
|||||||||||
|
|
(n 4)! |
|
|
|
|
|
|
|
|
|
|
||
б)1 Рассмотрим частный случай – уравнения второго порядка вида |
||||||||||||||
|
|
|
|
|
|
y |
|
f |
|
, |
|
(3.51) |
||
|
|
|
|
|
|
|
(x, y ) |
|
||||||
т.е. не содержащие искомую функцию y в явном виде. |
|
|
||||||||||||
Выполнив |
подстановку |
|
|
|
z(x) y , |
получим |
дифференциальное |
|||||||
уравнение: |
|
|
|
|
|
dz |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
f (x,z). |
|
|
(3.52) |
||||
|
|
|
|
|
|
|
dz |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если это дифференциальное уравнение является либо уравнением с |
||||||||||||||
разделяющимися переменными (т.е. |
f (x,z) f1(x) f2(z)), |
|
либо однородным |
|||||||||||
уравнением (т.е. |
f (x,z) f (z |
x)), или приводящимся к однородному, либо |
||||||||||||
___________________________________________________________________
1Материал этого пункта входит в обязательный минимум лекционного курса по дифференциальным уравнениям
90
линейным уравнением (т. е. f (x,z) p(x)z q(x)), либо уравнением Бернулли
(т.е. f (x,z) p(x)z q(x)zn), либо уравнением в полных дифференциалах (т.е. dz f (x,z)dx dU), то мы можем построить его общее решение, применяя описанные в гл. 2 процедуры.
Предположим, нам удалось найти общее решение уравнения (3.52) z (x,C1).
Это означает, что далее нам необходимо решить дифференциальное уравнение вида:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
(x,C ). |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Разделяя переменные и интегрируя, получим его общее решение: |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y (x,C1)dx C2. |
(3.53) |
||||||||||||||||||||||
|
|
Рассмотрим примеры интегрирования уравнений вида (3.51). |
||||||||||||||||||||||||||||||||||
|
|
Пример. |
Решить уравнение x3y x2y 1. |
|
||||||||||||||||||||||||||||||||
|
|
Решение. Вводим новую функцию z y , тогда y z . Подставив ее в |
||||||||||||||||||||||||||||||||||
уравнение, имеем |
|
|
|
|
|
|
|
|
|
x3z x2z 1. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p и его решение |
||||||||||||||||
|
|
Это линейное уравнение первого порядка относительно |
||||||||||||||||||||||||||||||||||
разыскиваем в виде произведения z uv |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
2 |
uv 1. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(u v |
uv ) x |
|
|
|
|||||||||||||||||||
|
|
Учитывая требования u(x3v x2v) 0, v(x) 0, находим функцию v(x): |
||||||||||||||||||||||||||||||||||
|
dv |
|
dx |
v |
1 |
, подставляем в уравнение для определения |
u(x) |
|||||||||||||||||||||||||||||
|
|
, |
|
|
||||||||||||||||||||||||||||||||
v |
x |
x |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3u |
1 |
|
1. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
C1. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
u |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
x |
|
|||||||||||||||||||||
|
|
Таким образом, p |
|
C1 |
|
|
1 |
|
, и можно найти функцию y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
y C1 |
dx |
|
dx |
, |
y C1ln |
|
x |
|
|
C2. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||
|
|
Пример. Проинтегрировать уравнение y 2y exy 2. |
|
|||||||||||||||||||||||||||||||||
|
|
Решение. |
|
|
Применяя |
|
|
|
подстановку |
|
|
z y , относительно z получим |
||||||||||||||||||||||||
уравнение Бернулли: z 2z exz2. Очевидно, последнее уравнение допускает решение z 0, откуда y C . Найдем общее решение уравнения Бернулли, применив метод Бернулли. Ищем решение уравнения в виде произведения
91

z u v, |
z |
|
|
|
|
|
|
|
|
Подставим |
в уравнение |
эти выражения, имеем: |
|
|
u v uv . |
||||||||||||
|
|
2uv |
e |
x |
u |
2 |
v |
2 |
. |
Потребовав, |
чтобы одна |
из введенных функций |
|
u v uv |
|
|
|
|
|||||||||
удовлетворяла однородному уравнению, получим систему уравнений с разделяющимися переменными
dv
2v 0,
dx
du exu2v.
dx
Интегрируя первое уравнение, получим
|
|
|
dv |
|
dx, |
|
|
|
|
|
~ |
|
|
|
|
|||
|
|
|
2 |
|
lnv 2x C1. |
|
|
|
|
|||||||||
|
|
v |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Частное решение берем в виде: |
v e 2x . |
|
|
|
|
|||||||||||||
Подставим эту функцию во второе уравнение системы. Получаем |
||||||||||||||||||
следующее дифференциальное уравнение |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
du |
|
x |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
e |
|
|
u |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||
Разделяя переменные и интегрируя, имеем: |
|
|
|
|
||||||||||||||
|
du |
e xdx C , |
|
1 |
e x C , |
u |
|
1 |
. |
|||||||||
|
|
|
|
|
||||||||||||||
u2 |
|
|
|
1 |
|
|
|
u |
|
|
1 |
|
e |
x C1 |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Учитывая замену, получим общее решение уравнения Бернулли:
1 |
, |
|
z |
|
|
ex C e2x |
||
1 |
|
|
или |
|
|
|
dy |
|
1 |
|
, |
y |
|
dx |
C2. |
|||
|
|
|
|
|
ex C e2x |
|||||||
|
dx ex C e2x |
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
||
Преобразуем интеграл к дробному виду |
|
|||||||||||
|
|
|
|
dx |
|
|
|
|
|
dex |
|
|
|
|
|
ex(1 C ex) |
e |
2x(1 C ex) |
|
|
|||||
|
|
|
|
|
1 |
|
|
1 |
|
|
||
и обозначим ex t. Подынтегральную функцию разложим на сумму простых дробей
|
|
1 |
|
A B |
|
D |
At(1 C t) B(1 C t) Dt2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
. |
t |
2 |
(1 C t) |
t |
t |
2 |
1 C t |
t |
2 |
(1 C t) |
|||||
|
|
|
|
|
1 |
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
Коэффициенты разложения найдем комбинированным методом. Из равенства
At(1 C1t) B(1 C1t) Dt2 1,
92
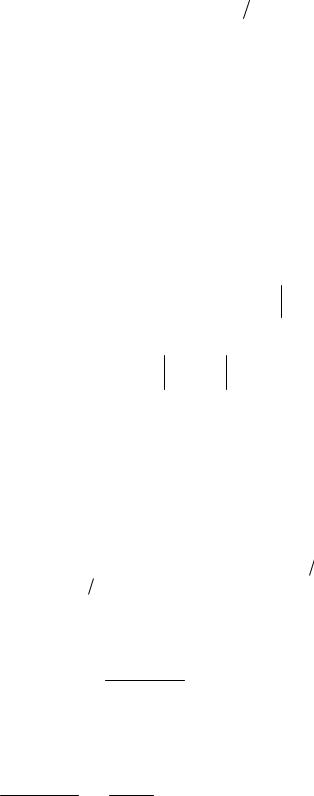
положив t 0, найдем |
B 1; |
положив t 1 C , найдем |
D C2 |
. Далее, |
|
|
1 |
1 |
|
приравнивая коэффициенты при t2 в правой и левой частях этого равенства, получим C1A C12 0, A C1.
Таким образом, получено разложение подынтегральной функции на простые дроби:
|
1 |
|
C1 |
|
|
1 |
|
C12 |
. |
e |
2x(1 C ex) |
ex |
e |
|
|
||||
|
|
2x |
|
1 C ex |
|||||
|
1 |
|
|
|
|
|
|
1 |
|
Вычислив интеграл
|
|
|
dx |
|
|
|
dex |
|
dex |
|
dex |
|
||||
|
|
|
|
|
C1 |
|
|
|
C12 |
|
|
C1lnex |
||||
e |
2x(1 C ex) |
ex |
(ex)2 |
1 C ex |
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
d(1 C ex) |
C1x e x C1ln1 C1ex |
|
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
C1 |
|
1 |
C2, |
||||||||
|
|
ex |
1 C |
ex |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
получаем общее решение уравнения:
y e x C1 ln1 C1ex x C2.
Решением уравнения является также функция y C и это решение не входит в семейство, описываемое общим решением.
Пример. Рассмотрим задачу геометрического характера. Найти все
кривые, кривизна которых в любой точке равна единице. |
|
|
||||||||||||
Решение. |
Воспользуемся |
известным |
из |
математического |
анализа |
|||||||||
выражением для |
кривизны |
линии |
y(x) |
и |
|
приравняем кривизну |
единице. |
|||||||
Получаем: |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
(1 y |
2 |
|
3 2 |
|
|
||
|
|
(1 y 2)3 |
2 1, |
или |
) |
. |
|
|||||||
|
|
|
|
|
|
|||||||||
Задача привела к дифференциальному уравнению 2-го порядка вида (3.51). Применяя подстановку y z, получим z (1 z2)3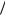 2. Откуда
2. Откуда
dz
(1 z2)3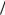 2 x C1.
2 x C1.
Интеграл вычисляем с помощью замены переменной z tgt;
dz dt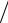 cos2 t , 1 z2 1
cos2 t , 1 z2 1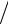 cos2 t. Получаем:
cos2 t. Получаем:
(1 zdz2)3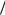 2 cosdt2 t (cos2 t)3
2 cosdt2 t (cos2 t)3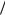 2 costdt sint.
2 costdt sint.
93

|
Возвращаясь |
|
|
к |
переменной |
|
|
|
|
z, |
используем |
формулу |
||||||||||||||||||||||
sint |
|
|
|
tgt |
|
|
|
|
|
z |
|
|
|
|
|
. Таким образом, получили общий интеграл уравнения |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
1 tg2t |
1 z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
для функции z (первый интеграл) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
x C1, откуда |
z |
|
|
|
|
x C1 |
|
, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 z2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 (x C )2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
или |
dy |
|
|
|
|
x C1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dx |
1 (x C1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Интегрируя, |
получаем |
2(x C )d(x C ) |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
y C2 |
|
1 |
|
1 |
|
1 (x C1) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 (x C1) |
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Возведем обе части равенства в квадрат, получим уравнение семейства |
|||||||||||||||||||||||||||||||||
искомых кривых: |
|
|
|
|
|
|
|
|
(x C )2 (y C |
|
)2 1. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
Искомые линии – окружности с радиусом, равным единице. 4. Уравнения, не содержащие независимой переменной.
а). Общий вид таких уравнений, разрешенных относительно старшей производной, следующий
|
|
|
|
|
|
y(n) |
|
f (y, y , y , , y(n 1)). |
|
|
|
|
|
|
|
(3.54) |
|||||||||||||||||||
Введем новую неизвестную функцию, зависящую от x посредством y: |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.55) |
||
|
|
|
|
|
|
|
|
|
|
|
z(y) y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Выразим производные по x функции y через функцию z и ее |
|||||||||||||||||||||||||||||||||||
производные по |
|
y. Имеем, используя правило дифференцирования |
сложной |
||||||||||||||||||||||||||||||||
функции: |
|
|
|
|
|
|
|
|
dy |
|
|
|
dz |
|
|
dz |
|
dy |
|
|
dz |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
y |
|
|
|
z |
, |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
dy |
dx |
|
dy |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dy |
|
d |
dz |
|
|
|
d |
dz |
|
|
dy |
|
d |
2 |
z |
dz |
2 |
|
|
|
||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
z, |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
dy2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
dx dy |
|
|
|
dy dy |
|
|
dy |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
По индукции заключаем, что производная |
|
порядка |
функции |
y |
|||||||||||||||||||||||||||||||
выражается через новую функцию |
z |
и ее производные |
по |
|
y |
до |
(n 1) - |
го |
|||||||||||||||||||||||||||
порядка включительно. Таким образом, получили выражения производных от y следующего вида:
y z |
dz |
y z2 |
d2z |
dz |
2 |
|||
|
, |
|
z |
|
|
, |
||
|
|
|
||||||
|
dy |
|
dy2 |
|
|
|
|
|
|
|
dy |
|
|||||
|
|
|
94 |
|
|
|
|
|
y(4) |
z3 |
d3z |
4z2 |
dz d2z |
dz |
3 |
||||
|
|
|
|
z |
|
|
, |
|||
|
|
|
|
|||||||
|
|
dy3 |
|
dy |
|
dy2 |
|
|
|
|
|
|
|
|
dy |
|
|||||
(3.56)
|
(n) zn 1 |
d |
n 1 |
z |
|
dz |
|
d |
n 2 |
z |
|
||
y |
|
|
z, |
, , |
|
|
. |
||||||
|
|
n 1 |
|
|
|
n 2 |
|||||||
|
|
dy |
|
dy |
|
dy |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
В результате подстановки выражений (3.55), (3.56) в уравнение (3.52), оно преобразуется к виду
|
|
|
|
|
|
d |
n 1 |
z |
|
|
|
|
|
dz |
d |
n 2 |
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(3.57) |
||||||||||||
|
|
|
|
|
|
dy |
n 1 |
F |
y,z, |
|
|
|
, , |
dy |
n 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
d |
n 2 |
z |
|
|
|
|
|
1 |
|
|
|
|
|
|
dz |
d |
n 2 |
z |
|
|
|
|
|
dz |
|
d |
n 2 |
z |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
F y,z, |
|
, , |
|
|
|
|
|
|
|
|
|
|
|
f |
|
y,z, |
|
|
|
, , |
|
|
|
|
|
|
|
|
|
z, |
|
|
, , |
|
|
|
. |
|||
|
|
n 2 |
|
|
|
n 1 |
|
|
|
|
|
|
n 2 |
|
|
|
n 2 |
|||||||||||||||||||||||
|
dy |
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
dy |
|
|
|
||||||||||||||||||||
|
|
dy |
|
z |
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
dy |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Полученное |
уравнение |
|
|
(3.57) имеет |
порядок, |
на |
единицу меньший |
|||||||||||||||||||||||||||||||||
порядка дифференциального уравнения (3.54). Если, интегрируя уравнение (3.57), удастся найти общее решение
|
z (y,C1, ,Cn 1), |
|
|
|||
то, возвращаясь к исходной функции y , получим уравнение: |
|
|||||
|
y (y,C1, ,Cn 1). |
|
(3.58) |
|||
Проинтегрировав его, найдем общий интеграл уравнения (3.54), |
||||||
выраженный в квадратурах |
|
|
|
|
|
|
|
dy |
|
|
x Cn. |
|
(3.59) |
(y,C , ,C |
n 1 |
) |
|
|||
1 |
|
|
y за |
|
||
В заключении отметим следующее. Принимая |
независимую |
|||||
переменную в (3.55), мы могли потерять решение вида |
y const . Поэтому в |
|||||
уравнении (3.54) нужно положить y C . В результате получим |
f (C,0, ,0) 0. |
|||||
Если это уравнение имеет корни C(1), ,C(m), то уравнение (3.54) допускает решения вида y C(k) (k 1,2, ,m), которые могут оказаться особыми решениями.
Далее, особые решения уравнения (3.57) могут привести к особым решениям уравнения (3.54) в силу подстановки (3.55). И, наконец, особые решения могут возникать при интегрировании уравнения (3.59).
б)1. Рассмотрим частный случай – уравнения второго порядка, не
содержащие независимое переменное: |
|
y f (y, y ). |
(3.60) |
____________________________________________________________________
1Материал этого пункта входит в обязательный минимум лекционного курса по дифференциальным уравнениям.
95
Выполним подстановку |
|
||||
|
|
z(y) y (x), |
(3.61) |
||
откуда y z |
dz |
. В результате подстановки уравнение (3.60) примет вид |
|
||
|
|
||||
|
dy |
|
|||
|
|
z |
dz |
f (y,z). |
(3.62) |
|
|
|
|||
|
|
|
dy |
|
|
Решая уравнение (3.62) найдем общее решение z (y,C1), являющееся первым интегралом (3.61).
Используя (3.61), получаем дифференциальное уравнение
|
|
|
|
|
|
|
|
dy |
(y,C ). |
|
|
|
|
|
(3.63) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Разделяя переменные и интегрируя, получим общий интеграл уравнения |
||||||||||||||||||||||||||||||||||
(3.60) |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x C2. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
(y,C ) |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Найти решения уравнения |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
(1 y2)yy (3y2 1)y 2. |
|
|
|||||||||||||||||||||||||||
Решение. |
|
Это |
дифференциальное |
|
|
|
|
уравнения 2-го порядка, не |
||||||||||||||||||||||||||
содержащее независимой переменной. |
Полагая |
y z(y), |
т.е. принимая y за |
|||||||||||||||||||||||||||||||
независимую переменную, имеем: y |
z |
dz |
. Уравнение принимает вид: |
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(1 y |
2 |
)yz |
(3y |
2 |
1)z |
2 |
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
dy |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда видно, |
что |
z 0, |
|
т.е. |
y 0 |
и |
|
y C , |
является решением |
|||||||||||||||||||||||||
уравнения. Разыскиваем ненулевые решения уравнения для z; |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
y(1 y |
2 |
) |
|
dz |
|
(3y |
2 |
1)z. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
dy |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Разделяя переменные, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
dz |
|
|
3y2 1 |
dy. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
y(1 y |
|
|
) |
|
|
|
|
|
|
||||||||
Разложим |
подынтегральную |
функцию |
|
|
в |
правой |
части равенства на |
|||||||||||||||||||||||||||
простые дроби: |
|
3y2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(1 y2) y(By D) |
||||||||||||
|
|
A By D |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(1 y2) |
|
|||||||||||
|
|
y(1 y2) |
y 1 y2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Отсюда, приравнивая числители, получим равенство:
A(1 y2) By2 Dy 3y2 1.
96

Полагая y 0, получаем A 1. Приравнивая коэффициенты при y и
y2, получим: |
|
|
|
|
|
|
A B 3, |
D 0, |
B 4. |
||||
Итак, разложение имеет вид: |
|
|
|
|
|
|
|
3y2 1 |
|
1 |
|
4y |
|
|
|
|
|
|
|
. |
|
y(1 y2) |
|
|
|||
|
|
y |
1 y2 |
|||
Подставив разложение под интеграл, имеем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
ln |
|
z |
|
ln |
|
y |
|
2 |
|
2ydy |
|
ln |
|
y |
|
|
2 |
d(1 y ) |
, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 y |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
z |
|
|
|
ln |
|
y |
|
2ln(1 y2) ln |
|
C |
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Отсюда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yy |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zy |
|
|
|
|
|
|
|
|
|
|
|
|
C , |
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C . |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(1 y2)2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 y2)2 |
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Итак, первый интеграл уравнения получен. Интегрируя еще раз, найдем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
общий интеграл: |
|
|
|
2ydy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
C1 dx C2 , |
|
|
|
1 |
|
|
|
|
1 |
|
C1x C2, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
(1 y |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 y |
|
|
|
|
|
|
||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 y2 |
|
~ |
~ |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1x C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
где |
|
2C2. |
|
|
Из общего интеграла решение |
y C получается, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
C1 2C1, |
C2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
если положить C~1 0. Решение y 0 получается при |
~ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
C2 . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример. |
Найти решение |
|
задачи |
|
Коши: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4y |
|
|
|
y 1, |
|
|
y(0) 1, |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) 1. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Это уравнение не содержит х и, следовательно, относится к |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
типу |
(3.54). Делая |
|
замену |
|
|
|
|
|
y z(y), |
y z |
dz |
|
|
|
|
|
|
и |
подставляя в уравнение, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dy |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
4zdz |
|
|
|
|
|
, |
2z2 2 |
|
2C , |
|
z2 |
|
C . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
y |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Подставляя начальные данные y(0) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, найдем |
C1 0. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y |
(0) z(1) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
z |
|
|
|
y . Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Поскольку y (0) 1 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
x C2. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx, |
|
|
|
|
|
|
|
|
|
y3 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
97

Подставляя x0 0, |
y(0) 1, получим |
C2 |
|
4 |
, после чего найдем у |
|
|||||
|
|
|
3 |
|
|
y3
 1 3 x 4.
1 3 x 4.
4
Вопросы для самоконтроля
1. Сформулируйте теорему о существовании и единственности решения дифференциального уравнения n-го порядка. Как эта теорема формулируется для уравнения 2-го порядка.
|
|
2. |
Изложите |
метод |
решения |
дифференциального |
|
уравнения |
вида |
||||||||||||||
y(n) f (x). Напишите формулу общего решения уравнения |
y |
f (x). |
|||||||||||||||||||||
Приведите пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3. |
Изложите |
метод |
решения |
дифференциального |
|
уравнения |
вида |
||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x,y ). Приведите пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
4. |
Изложите |
метод |
решения |
дифференциального |
|
уравнения |
вида |
||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (y, y ). Приведите пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
5. Напишите пример линейного дифференциального уравнения. |
|
|
|||||||||||||||||||
|
|
|
|
|
Задачи для практических занятий и самостоятельного решения |
||||||||||||||||||
1. |
y x, |
|
y(1) 1, |
y (1) |
2. |
|
Ответ: |
y |
x3 |
|
|
3 |
x |
2 |
. |
|
|
|
|
|
|||
|
|
6 |
|
2 |
3 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
y |
lnx |
, y(1) 0, |
y (1) |
1, |
y (1) 2. |
Ответ: |
y |
x2 |
ln2 x |
3 |
x2 |
2x |
1 |
. |
||||||||
|
|
|
2 |
||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||
3.y x cosx.
4.y 2xln x.
5.xln x y y .
6.xy y .
7.xy (1 2x2)y .
8.xy y ln y .
x
Ответ: |
y |
x4 |
|
sinx C x2 |
C |
2 |
x C . |
|||||||||||||||||
|
|
|
||||||||||||||||||||||
|
24 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
y |
x3 |
lnx |
|
5 |
x3 C x C |
2 |
. |
||||||||||||||||
|
|
|||||||||||||||||||||||
|
3 |
|
|
|
18 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
y (C x C 2)eC1 |
|
C |
2 |
. |
|
||||||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
y C x2 C |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: |
y C ex2 |
C |
2 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
y (C x C2)eC1 |
|
C |
2 |
. |
|
||||||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
98
9. |
2y |
|
|
|
|
y |
|
|
x2 |
|
|
y(1) |
|
|
|
2 |
|
|
|
|
2 |
|
|
Ответ: |
y |
2 |
x5 2. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
, |
|
|
, |
. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
|
|
|
|
|
|
5 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
(C x C |
2 |
)2 |
||||||||||
|
|
2yy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: y |
1 |
|
|
|
|
|
|
. |
||||||||||||||||
|
|
|
|
1 (y ) . |
|
|
|
|
|
|
4 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
y |
|
2y |
3 |
, y(0) 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
11. |
|
|
|
|
|
|
|
|
Ответ: y |
|
. |
|
|
|||||||||||||||||||||||||||
|
|
y (0) 1. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|||||||
12. |
2yy |
|
y |
y |
4, |
|
y(0) 1, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
y (0) 2. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
8 |
|
5 |
||
|
|
|
|
|
|
|
|
|
|||
Ответ: 15 |
|
4 |
|||
|
|
|
|
1 |
|
y |
|
|
|||
5 |
|||||
|
|
|
|
||
3 2
2
y 1 x C2 общий интеграл.
(15x 1)2 3 4. 5
3 4. 5
13. |
yy y 2 y2 ln y (считая y 0, y 0). |
|
|
|
|
|
|
|
|
|||||||
|
|
|
C |
ln2 |
y C2e2x |
2C |
2 |
ex ln y ln2 |
y или |
|||||||
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
C2e2x |
C |
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
y exp |
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
ex |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2C |
2 |
|
|
|
|
|
||
|
y y (1 y ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
14. |
Ответ: y C2 |
|
|
|
|
|||||||||||
ln1 exp(x C1) |
. |
|
||||||||||||||
15. |
yy y (1 y ). |
Ответ: |
y |
1 |
|
(1 C2eC1x). |
|
|
|
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|||
16.yy 1 y 2. Ответ: y C1ch x C2 .
C1
17. y 3yy , |
y(0) y (0) 1, y (0) |
3 |
. |
Ответ: |
y |
4 |
. |
2 |
(x 2)2 |
4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
4.1. Линейные дифференциальные уравнения второго порядка
Линейные дифференциальные уравнения второго порядка в теории дифференциальных уравнений занимают важное место не только потому, что представляют собой простой и хорошо изученный тип уравнений, но и потому, что многие практические задачи физики, механики, техники и особенно электротехники приводят к решению этих уравнений.
1. Основные понятия Определение. Уравнение вида
y p(x)y q(x)y f (x), |
(4.1) |
99 |
|
