Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 800446

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

2.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 199 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

путем n кратного дифференцирования уравнения (3.16) с последующим исключением параметров из полученной системы n 1 уравнений.

Таким образом, можно считать, что общее решение дифференциального уравнения n-го порядка должно содержать n независимых параметров

C1,C2, ,Cn.

Общим решением дифференциального уравнения n-го порядка называется функция вида (3.15), зависящая от n независимых переменных, из которого при соответствующих значениях этих параметров могут быть получены все решения уравнения, кроме особых.

Приведем более подробное определение, в котором “расшифрованы” все

условия, содержащиеся в выше приведенном.

Пусть D - область в

каждой точке которой

задача

Коши

для

уравнения (3.15)

имеет

единственное

решение.

Функция (3.16),

где

C1,C2, ,Cn -

произвольные

постоянные,

называется

общим

решением

уравнения (3.15) в области D, если:

1) функция имеет непрерывные частные производные по

x до n-го

порядка включительно;

2) для любой точки M0(x0, y0, y0, , y0(n 1)) D система n уравнений

y0 (x0,C1,C2, ,Cn),

(3.17)

(n 1)

(n 1)(x

, ,C

)

единственным образом разрешима относительно C1, ,Cn :

		C10 1(x0, y0, y0, , y0(n 1)),
		C20 2(x0, y0, y0, , y0(n 1)),							(3.18)
		Cn0 n(x0, y0, y0, , y0(n 1));
3) функция (x,C10, ,Cn0) является решением уравнения (3.15) при
любых значениях	произвольных постоянных			C10, ,Cn0,		когда			точка
M0(x0, y0, y0, , y0(n 1)) принадлежит области D.
Замечание.	Если в формуле общего решения (3.16) роль произвольных
постоянных C1, ,Cn		играют начальные значения			y0, y0, , y0(n 1)			искомой
функции y(x) и	ее	первых n 1	производных				(n 1)	(x) при
					y (x), , y
некотором фиксированном значении			аргумента	x x0 , то		формула			(3.16),
принимающая вид

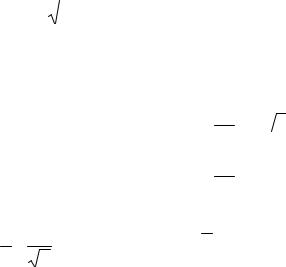
	y (x,x0;y0,y0, ,y0(n 1)),	(3.19)
называется общим решением в форме Коши.
Интегрируя уравнение (3.15) редко удается получить решение,
зависящее	от n произвольных параметров, в виде (3.16).	В большинстве
случаев n	- параметрическое семейство интегральных кривых получается в

неявном виде (в виде, не разрешенном относительно неизвестной функции y ):

Ф(x, y,C1,C2, ,Cn) 0.	(3.20)
Такая форма решения называется общим интегралом уравнения.
Частным решением дифференциального уравнения (3.15)	называются

решения, полученные из общего решения при частных числовых значениях произвольных постоянных C1, ,Cn, включая случай, когда значения этих

констант равны : y (x,C10, ,Cn0).

Аналогично вводится понятие частного интеграла – это решение в неявном виде, полученное из общего интеграла (3.20) при частных значениях


параметров C C		0,	, C	n	C	0:
1	1					n
Особым	решением				Ф(x, y,C10, ,Cn0) 0.		(3.21)
					называется такое решение уравнения, в каждой
точке которого нарушается единственность решения задачи Коши.
Уравнение		n го порядка (3.15) может иметь семейство					особых

решений, зависящее от произвольных постоянных, число которых может

доходить до n 1.
Пример.		Найти решения	дифференциального	уравнения второго
порядка y 2		.
порядка y 2	y	.
Решение.	Введем новую неизвестную функцию			z(x) y (x). Отсюда
y z . Выраженное через новую			функцию дифференциальное уравнение

будет эквивалентно системе уравнений с разделяющимися переменными:

2 z,

dy z.dx

Из первого уравнения системы получим:

12 dzz dx (z 0), z x C1, z (x C1)2 при x C1.

Другим решением этого уравнения является функция z 0.

Подставим найденные функции во второе уравнение. Получим совокупность уравнений

dy		(x C )2	,
		(x C )2	,
		1

dx
	dy	0.
		0.
dx

Интегрируя эти уравнения, будем иметь:

y	1	(x C )			3 C	2	(x C );	y C.

	3		1				1
							y C не
Таким образом, семейство				решений				получается из общего

решения уравнения ни при каких значениях постоянных C1 и C2. Каждая из линий этого семейства является особым решением уравнения.

Итак, для данного дифференциального уравнения получено общее решение – двухпараметрическое семейство интегральных кривых, а также построены особые решения.

Пример. Для дифференциального уравнения, заданного в предыдущем примере, найти частное решение, удовлетворяющее начальным условиям: y(0) 1, y (0) 0.

Решение. Из общего решения уравнения и его производной получим систему уравнений для нахождения постоянных C1 и C2:

y(0)

(x C1)3 C2

x 0,

dy(0)

(x C1)

)

x 0;

C1 0,

C2 1.

Подставляя найденные постоянные в формулу для общего решения, получим частное решение, удовлетворяющее заданным начальным условиям:

y x3 1. 3

3.3. Уравнения высших порядков, интегрируемые в квадратурах. Уравнения, допускающие понижения порядка

1. Из того, что дифференциальное уравнение n-го порядка (3.15) имеет решение, вовсе не следует, что решение выражается в квадратурах. Это замечание относится даже к уравнениям первого порядка. В этом параграфе будут указаны некоторые виды уравнений n-го порядка, общий интеграл которых, (или общее решение) можно найти при помощи квадратур.

Интегрирование таких уравнений будет осуществляться сведением к уравнениям низшего порядка. При такой процедуре порядки промежуточных

дифференциальных уравнений постепенно понижаются, а число входящих в них параметров C1,C2, (“произвольных постоянных”) – увеличивается. Интегрирование уравнения будет закончено когда получается общий интеграл Ф(x, y,C1, ,Cn) 0, не содержащий производных искомой функции и включающий n произвольных постоянных.

Ниже будем рассматривать неполные уравнения, т.е. уравнения вида (3.15) но такие, в которых функция, стоящая в правой части, зависит только от некоторых аргументов.

2.Уравнение, содержащее старшую производную неизвестной функции

изаданную функцию от x.

а) Рассмотрим решение уравнения (3.15) в том случае, когда в правой части функция зависит только от x, то есть уравнения вида

y(n) (x),	(3.22)
где, функция (x) непрерывна в некотором интервале	(a,b). Представляя


производную в форме y(n) y(n 1) , можно записать уравнение (3.22) так:
			dy(n 1)
					(x),
					(x),
откуда			dx
откуда				x
				x
		y(n 1)		(x)dx C1,				(3.23)
				x0
где C1 - произвольная постоянная,				x (a,b), x0 - любое фиксированное число
из промежутка (a,b). Рассуждая аналогично, находим
	x		s2
y(n 2) ds2 (s1)ds1 C1(x x0) C2,
	x0		x0
x	s3	s2				C1
y(n 3) ds3 ds2 (s1)ds1						C1	(x x0)2 C2(x x0) C3,
y(n 3) ds3 ds2 (s1)ds1							(x x0)2 C2(x x0) C3,
x0	x0	x0		2
x0	x0	x0

	x	s2

	y dsn (s1)ds1
	x0	x0
x	s2	C1
y dsn (s1)ds1		C1
			(x
		(n 1)!	(x
x0	x0

(3.24)

(x x )n 2

(x x )n 3

C ,

(n 2)!

(n 3)!

n 1

x )n 1

(x x )n 2

n 1

(x x ) C .

(n 2)!

Последняя из формул (3.24) содержит все решения уравнения (3.22) в

области a x b,	y ,	y ,	, y(n 1)	и
представляет собой общее решение уравнения.
З а м е ч а н и е. Функция		s2
	x	s2
	Y(x) dsn (s1)ds1			(3.25)
	x0	x0

является частным решением уравнения (3.21), поскольку получается из общего решения при C1 C2 Cn 0.

Выражение для функции (3.25) можно упростить, если воспользоваться следующими соображениями. Введем следующую последовательность функций

K1(x,x0) (s1)ds1, x0

x	x	s2					x	s2
K2(x,x0) K1(s2,x0)ds2							ds2 (s1)ds1,
K2(x,x0) K1(s2,x0)ds2		(s1)ds1 ds2					ds2 (s1)ds1,
x	x	x					x	x
0	0			0			0	0
x	x		s		s
K3(x,x0) K2(s3,x0)ds3				3		2
K3(x,x0) K2(s3,x0)ds3						(s1)ds1 ds2 ds3,
x	x		x		x
0	0			0		0

(3.26)

x	x	sn 1	s2
Kn 1(x,x0) Kn 2(sn 1,x0)dsn 1 dsn 1 dsn 2 (s1)ds1,
x0	x0	x0	x0
x

Y(x) Kn 1(sn,x0)dsn, x0

где индекс у K -функций нумерует число квадратур в формуле, определяющей эти функции.

Упростим сначала формулу для функции K2(x,x0), рассматривая последнее интегральное выражение в этой формуле как повторный интеграл, равный соответствующему двойному интегралу по области D21 x0 s1 s2, x0 s2 x на плоскости S2OS1 (см. рис. 10):

x s2

ds2	(s1)ds1	(s1)ds1ds2.	(3.27)
x0	x0	D21
		84

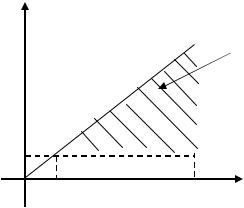
Область интегрирования K2(x,x0). Область ограничена линиями: s1 x0,s1 s2, s2 x0 , s2 x.

x			D21
x

	s1 s2
x0			s2
x0	x0	x
0	x0	x

Рис. 10

Двойной интеграл в правой части равенства (3.27) запишем в виде повторного интеграла, но с измененным порядком интегрирования относительно повторного интеграла в левой части этого равенства. Имеем:

(s1)ds1ds2 ds1 (s1) ds2 ds1 (s1)s2

(x s1) (s1)ds1.

Таким образом,

выражение для функции K2(x,x0) записывается в виде

одной квадратуры

K2(x,x0) (x s) (s)ds,

(3.28)

где переобозначили переменную интегрирования s1 s.

Для функции K3(x,x0)

упрощенное выражение получаем в результате

выполнения аналогичных процедур на плоскости S3OS :

K3(x,x0) K2(s3,x0)ds3 ds3 (s3 s) (s)ds

(s2 s) (s)ds3ds

ds (s)

(s3 s)ds3 ,

D31

где область D31-та же , что на рис. 10, с переобозначением осей координат. Вычислив интеграл по s3, получим выражение для функции K3 в виде одной квадратуры:

K3(x,x0) 12 (x s)2 (s)ds. x0

Дальнейшее применение описанного выше алгоритма приводит к выражениям:

(x s)3 (s)ds,

(x s)n 2 (s)ds,

K4(x,x0)

Kn 1(x,x0)

2 3

(n 2)!

n 1

(3.29)

Y(x) (n 1)! (x s)

(s)ds.

Таким образом, общему решению (3.24) уравнения (3.22) с учетом (3.29)

можно придать следующий вид:

n 1

(x x0)n k

(x s)

(s)ds Ck

(n 1)!

(n k)!

k 1

(3.30)

(x x0)n 1

(x s)

n 1

(s)ds C1

(n 1)!

(x x0 )n 2

Cn 1(x x0 ) Cn ,

(n 2)!

где, как известно,

0! 1,

x0 - произвольная фиксированная точка из (a,b),

x (a,b), Ck

(k 1,2, ,n)- произвольные постоянные. Еще раз подчеркнем –

общее решение (3.30) дифференциального уравнения (3.22) содержит все решения этого уравнения.

Формула (3.30), представляющая общее решение уравнения (3.22), позволяет найти решение с любыми начальными значениями искомой функции и ее производных до (n 1)- го порядка включительно.

Пусть задана задача Коши
		y(n) (x),	(3.31)
	y(x0) y0,	y (x0) y0, , y(n 1)(x0) y0(n 1),
где x0 (a,b),	y0, y0, , y0(n 1) - произвольные заданные числа.

Для определения значений постоянных положим в формулах (3.23), (3.24) и (3.30) x x0 и подставим в левые части соответствующие значения y и производных при x x0 из (3.31). Из формулы (3.23) получаем:

y0(n 1)	x0	C10 y0(n 1),
y0(n 1)	(x)dx C1,	C10 y0(n 1),	(3.32)
	x0

где использовали равенство нулю определенного интеграла с одинаковыми верхним и нижним пределами интегрирования.

Первое из выражений в формулах (3.24) позволяет найти C2

x	s
0		2	C20 y0(n 2),
y0(n 2)		(s)ds ds2 C1(x x0) C2,	C20 y0(n 2),	(3.33)
x	x
0		0
остальные формулы этого блока определяют постоянные
		C30 y0(n 3), Cn0 1 y0.		(3.34)

Последнюю константу найдем аналогично из формулы (3.30): Cn0 y0. Таким образом, найдены все значения постоянных, входящих в решение уравнения. Собирая результаты вычислений (3.32)-(3.34), имеем:

Ck0 y0(n k) (k 1, ,n), или в подробностях:

C10 y0(n 1),

C20 y0(n 2), ,Cn0 1

y0, Cn0 y0.

(3.35)

Решение задачи Коши (3.31) получаем подстановкой найденных

постоянных (3.35) в общее решение (3.30) уравнения (3.22):

(x x

)n k

(n k)

(s)ds y0

(3.36)

y (n 1)! (x s)

(n k)! .

k 1

З а м е ч а н и е.

Иногда функцию (3.36) называют общим решением

уравнения (3.22) в форме Коши. Однако в этом случае числа y0, y0

, , y0(n 1) в

формуле (3.36) являются произвольными постоянными.

б1. Рассмотрим частный случай – уравнения второго порядка вида

y (x).

(3.37)

Пример. Среди всех интегральных кривых уравнения y 6x выделить ту, которая в начале координат касается прямой y x.

1.	Решение.		Поскольку		искомая	интегральная кривая должна
проходить через начало координат,					то y(0) 0 - является первым условием.
Прямая	y x	с угловым коэффициентом k 1 должна быть касательной к
искомой линии		y(x)	в начале координат. Поэтому, y (0) 1. Таким образом,
получили задачу Коши
			y	6x,	y(0) 0,
						y (0) 1.

________________________________________________________________

1Материал этого пункта входит в обязательный минимум лекционного курса по дифференциальным уравнениям

Введем новую	функцию z(x) y (x).						Тогда z y .		Заданное
дифференциальное	уравнение			сводится			к	следующей	системе
дифференциальных уравнений 1-го порядка:
		dz	6x,		dy	z.

		dx			dx
Решение первого уравнения имеет вид z(x) 3x2 C1. Поскольку z y ,
то z(0) 1. Подставим в полученное решение x 0,								z(0) 1, получим C1 1.

Решаем второе уравнение, подставив в его правую часть z 3x2 1. Получим:

y (3x2 1)dx C2,	y x3 x C2.
Полагая, x 0, y(0) 0, получим	C2 0. Искомая интегральная кривая
уравнения: y x3 x.

2. Уравнение, не содержащее искомой функции и уравнение, не содержащее искомой функции, и нескольких первых производных.

В этом разделе будут рассмотрены несколько типов уравнений,

допускающих понижение порядка.

а) рассмотрим дифференциальное уравнение вида

y(n) f (x, y(m), y(m 1), , y(n 1))					(1 m n 1),		(3.38)
причем, производная m-го порядка обязательно входит в уравнение.
Введем новую неизвестную функцию
		z(x) y(m).					(3.39)
Тогда y(n) z(n m),		y(n 1) z(n m 1), , y(m 1) z и уравнение
(3.38) запишется в следующем виде
z	(n m)			(n m 1)		.	(3.40)
z		f (x,z,z , ,z				.	(3.40)
Это уравнение (n m)-го порядка . Введением замены (3.39) удалось
понизить порядок уравнения на m единиц.
Пусть интегрируя уравнение (3.40), мы нашли его общее решение
	z g(x,C1, ,Cn m).						(3.41)
В силу (3.39) это означает, что получено уравнение для функции							y(x)
вида:	y(m)
	y(m)	g(x,C , ,C	n m		).		(3.42)
		1	n m

Уравнение (3.42) относится к типу, уже изученному в п. 2 настоящего параграфа. Применяя метод, развитый для решения уравнения (3.31), получим формулу для общего решения уравнения (3.38) (аналог формулы (3.30)):

(x s)m 1g(s,C , ,C

)ds

(m 1)!

n m

(3.43)

(x x )m 1

Cn m 1

Cn 1(x x0) Cn.

(m 1)!

Отдельно рассмотрим два частных случая уравнения вида (3.38).

а. 1. Рассмотрим уравнение вида:

y(n) f (y(n 1)).

(3.44)

Применяя

подстановку

z(x) y(n 1) , получаем уравнение

первого

порядка:

f (z).

Интегрируя, находим первый интеграл уравнения:

x C .

f (z)

Предполагая возможным разрешение этого уравнения в элементарных

функциях относительно z(x), получаем

или

z (x,C1)

y(n 1) (x,C ).

(3.45)

Полученное уравнение относится к изученному типу (3.31). Используя

формулу для общего решения (3.30), получим:

n 2

(x x )n 2

(x s)

(s,C1)ds C2

Cn 1(x x0) Cn.

(3.46)

(n 2)!

Формула (3.46) дает общее решение уравнения (3.44).

а. 2.

Еще один тип уравнений, разрешаемых в квадратурах и

представляющих собой частный случай уравнения (3.38), имеет вид:

y(n) f (y(n 2)).

(3.47)

Применяя

подстановку

z(x) y(n 2),

получаем дифференциальное

уравнение второго порядка:

f (z).

(3.48)

Уравнения такого вида встречаются в механике при изучении движения материальной точки. Понижение порядка уравнения до первого проводится следующим приемом. Умножим обе части равенства (3.48) на 2z dx. Учитывая, что

	2			2	,
2z z dx ((z )		)	dx d(z )		,	z dx dz,

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 199 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20222.68 Mб6Учебное пособие 800441.pdf
#
01.05.20222.72 Mб1Учебное пособие 800442.pdf
#
01.05.20222.75 Mб14Учебное пособие 800443.pdf
#
01.05.20222.76 Mб2Учебное пособие 800444.pdf
#
01.05.20222.76 Mб4Учебное пособие 800445.pdf
#
01.05.20222.77 Mб7Учебное пособие 800446.pdf
#
01.05.20222.8 Mб7Учебное пособие 800447.pdf
#
01.05.20222.82 Mб3Учебное пособие 800448.pdf
#
01.05.20222.85 Mб2Учебное пособие 800449.pdf
#
01.05.2022355.3 Кб7Учебное пособие 80045.pdf
#
01.05.20222.85 Mб1Учебное пособие 800450.pdf