Учебное пособие 800446

где K - положительное число, M(x, y1, , yn) D. Тогда система имеет единственное решение

y1 1(x), , yn n(x),

удовлетворяющее начальным условиям y1 y1(0), , yn yn(0) при x x0. Это решение определено и непрерывно дифференцируемо (все k (x) имеют непрерывные производные) в интервале x x0 h, где h min a,b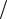M .

3. Понятие общего, частного и особого решений.

Вупрощенной формулировке общее решение системы (5.1)

определяется как семейство решений этой системы, зависящее от n

yn n(x,C1, ,Cn).

Геометрически общее решение есть семейство интегральных кривых в (n 1)-мерном пространстве x, y1, , yn, зависящее от n параметров

C1,C2, ,Cn, причем уравнения этого семейства линий разрешены

относительно y1, ,yn.

Частное решение системы – это такое решение, которое состоит из точек единственности решения задачи Коши.

Решение, получаемое из общего решения при определенных числовых значениях параметров C1,C2, ,Cn, включая , является частным решением.

Особым решением называется такое, в каждой точке которого нарушается единственность решения задачи Коши.

Пример. Найти решение системы

Решение. Заданная система, представляет собой совокупность зацепляющихся уравнений – одно из них можно решить независимо от другого. Интегрируем второе уравнение, разделяя переменные

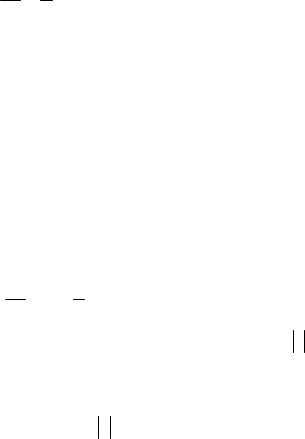
Подставим найденную функцию в первое уравнение

dy 2 y C1. dx x

Полученное уравнение является линейным дифференциальным уравнением 1-го порядка. Его решение найдем методом Бернулли: y uv, y u v uv ,

Второе уравнение системы (5.9) имеет особое решение z 0. Подставим его в первое уравнение, получим

dy x 2 y. dx x

Решая это уравнение методом Бернулли, получим y x2 C ln x . Итак,

система (5.9) помимо общего решения имеет еще семейство решений

z 0,

y x2 C ln x .

5.3.Интегрирование системы дифференциальных уравнений сведением

кодному уравнению n–го порядка

Впредыдущих разделах 5–й главы рассматривались примеры нахождения решений систем уравнений. Однако используемые там приемы интегрирования не были систематическими, а носили скорее характер ”ad hoc”.

Вэтом разделе будет рассмотрен один из основных методов интегрирования системы дифференциальных уравнений.

Суть используемого здесь метода заключается в следующем: из уравнений системы и из уравнений, получающихся дифференцированием уравнений системы, исключаются все искомые функции, кроме одной. Для определения этой функции получают одно дифференциальное уравнение n–го порядка (в случае системы из n уравнений). Из полученного уравнения находится одна неизвестная функция, а остальные искомые функции находятся из исходных уравнений и уравнений, получившихся в результате их дифференцирования.

1. Общий случай нормальной системы.

Рассмотрим схему приведения системы к одному дифференциальному уравнению n – го порядка в случае системы вида (5.1):

121

их значения, взятые из правых частей уравнений (5.10), мы получим следующие уравнения:

122

использовать систему (5.11), рассматривая ее как систему алгебраических уравнений относительно неизвестных y2, , yn . Требуем, чтобы эта система была разрешима относительно указанных неизвестных. Из математического анализа известно, что для разрешимости такой системы уравнений требуется выполнение условия

(5.11).

Можно показать (мы на этом не останавливаемся), что при сделанных предположениях, решение y1(x), найденное из (5.14) а также функции y2, , yn , найденные из (5.11), в совокупности будут являться решением

123

системы уравнений (5.10). И наоборот – решение системы (5.10) будет являться решением уравнения (5.14) и системы (5.11).

Пример. Решить систему уравнений

Решение. Дифференцируя обе части первого уравнения, получим:

Подставим эти выражения в предыдущее уравнение и присоединим выражение для z, найденное из 1-го уравнения:

dx

Для решения уравнения 2-го порядка представим его в виде:

d (y x) C1(y x). dx

Интегрируя, имеем: y x C2eC1x, C1 0, C2 , . Находим вторую неизвестную функцию:

dx

Таким образом, решение системы имеет вид: