
Учебное пособие 800446
.pdf2.7. Приведение некоторых дифференциальных уравнений к виду уравнения в полных дифференциалах. Интегрирующий множитель
Если условие (2.68) для коэффициентов в уравнении (2.62) не выполнено,
то есть |
P |
|
Q |
, то уравнение (2.62) не является уравнением в полных |
|
|
|||
|
y |
x |
||
дифференциалах. Естественно возникает вопрос: можно ли уравнение не в полных дифференциалах привести к виду уравнения в полных дифференциалах.
1. Введем понятие интегрирующего множителя.
Оказывается, что в ряде случаев уравнение вида (2.62) можно привести к уравнению в полных дифференциалах. Идея такого приведения состоит в
нахождении такой функции |
(x, y), называемой интегрирующим |
|
множителем, после умножения, на которую уравнение |
|
|
P(x, y)dx Q(x, y)dy 0 |
(2.78) |
|
преобразуется в уравнение |
|
|
(x, y)P(x, y)dx (x, y)Q(x, y)dy 0 |
(2.79) |
|
в полных дифференциалах, то есть |
|
|
Pdx Qdy dU(x, y). |
(2.80) |
|
В п. 2.6 показано, что необходимым и достаточным условием этого является соотношение (2.68), которое в рассматриваемом случае принимает вид
|
( P) |
|
( Q). |
(2.81) |
|
|
|||
y |
x |
|
||
Равенство (2.81) рассматривается как дифференциальное уравнение, решением которого является интегрирующий множитель (x, y). Выполняя дифференцирование, получим:
|
(x, y) |
|
(x, y) |
P(x, y) |
Q(x, y) |
(2.82) |
|||
Q(x, y) |
|
P(x, y) |
|
(x, y) |
|
|
|
. |
|
x |
y |
|
x |
||||||
|
|
|
y |
|
|
||||
Полученное уравнение содержит неизвестную функцию (x, y), и ее частные производные по x и по y, то есть является дифференциальным уравнением в частных производных. Решение такого уравнения представляет более сложную задачу, чем решение исходного уравнения (2.78). Далеко не всегда из уравнения (2.82) удается найти интегрирующий множитель и выразить с помощью квадратур.
2. Построение интегрирующего множителя в частных случаях.
Достаточно просто интегрирующий множитель находится в случаях, когда он является функцией одной переменной - x или y.
50

Рассмотрим сначала случай интегрирующего множителя, зависящего только от x. Пусть уравнение (2.78) имеет интегрирующий множитель вида(x). Тогда уравнение (2.82) упрощается и имеет вид
|
|
|
d (x) |
P(x,y) |
Q(x,y) |
(2.83) |
||||
|
Q(x, y) |
|
(x, y) |
|
|
|
, |
|||
|
|
|
|
|||||||
|
|
|
dx |
|
y |
x |
|
|
||
|
|
|
|
|
|
|||||
поскольку |
0. Уравнение |
(2.83) |
является |
обыкновенным |
||||||
|
||||||||||
|
y |
|
|
|
|
|
|
|||
дифференциальным уравнением. Из (2.83) разделяя переменные, имеем:
d |
1 |
P(x, y) |
Q(x, y) |
(2.84) |
||||
|
|
|
|
|
|
|
dx. |
|
|
|
|
|
|||||
|
|
|
y |
x |
|
|
||
Q(x, y) |
|
|
||||||
По предположению функция зависит только от x. Поэтому только от x зависит левая часть дифференциального равенства, а, следовательно, и правая часть этого равенства. Таким образом, для существования интегрирующего множителя вида (x) необходимо, чтобы
|
|
|
1 |
|
P(x,y) |
|
Q(x,y) |
(x). |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
y |
|
x |
|
|
||
|
|
|
Q(x,y) |
|
|
|
|
|||||||
Запишем уравнение (2.84) в виде |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
d |
(x)dx. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интегрируя это уравнение, |
получим |
|
|
|||||||||||
|
d |
|
|
|
|
(x)dx C, |
(x) Cexp( (x)dx). |
|||||||
|
|
|
|
|
||||||||||
|
|
(x)dx, |
ln |
|
|
|||||||||
|
||||||||||||||
|
|
|
|
|||||||||||
(2.85)
(2.86)
Обычно в выражении (2.86) берется частное значение C 1.
Покажем, что при выполнении условия (2.85) функция (2.86) превращает уравнение (2.78) в уравнение в полных дифференциалах. Используем признак
(2.81), имеем:
e (x)dxP(x, y) e (x)dx P(x, y),
y y
e (x)dxQ(x, y) e (x)dx (x)Q(x, y) e (x)dx Q(x, y).
x x
Преобразуем второе выражение, используя равенство (2.85). Получим:
x e (x)dxQ(x,y) e (x)dx Py Qx e (x)dx Qx e (x)dx Py .
Таким образом, условие (2.81) выполнено и уравнение (2.79) для нашего случая будет являться уравнением в полных дифференциалах.
Итак, доказано утверждение:
51
Для того чтобы дифференциальное уравнение (2.78) имело
интегрирующий множитель, |
|
зависящий |
от |
x, |
необходимо и достаточно, |
|||||||||||||||||||||||
|
|
1 |
|
P |
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
чтобы выражение |
|
|
|
было функцией только от x. В этом случае |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
интегрирующий множитель находится по формуле: |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
P |
|
Q |
|
|
|||||||
|
|
|
|
|
(x) exp |
|
|
|
|
|
|
|
|
dx . |
(2.87) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||
Пример. Найти |
|
|
|
|
|
|
|
|
|
|
|
Q |
|
x |
|
|
||||||||||||
|
|
|
интегрирующий |
множитель линейного |
уравнения |
|||||||||||||||||||||||
y p(x)y q(x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Запишем уравнение в симметрической форме: |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
p(x)y q(x) dx dy 0. |
|
|||||||||||||||||||
Проверим выполнимость условия (2.85): |
|
|
|
|
|
|
||||||||||||||||||||||
|
P(x, y) |
|
|
|
p(x)y q(x) p(x), |
|
Q(x, y) |
0, |
|
|||||||||||||||||||
|
|
y |
|
|
||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||
|
|
|
|
1 |
|
|
P |
|
Q |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
P(x) (x). |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, функция (x) exp( p(x)dx) является интегрирующим
множителем линейного уравнения 1-го порядка.
Найдем теперь условие, при котором интегрирующий множитель
зависит только от y. В этом случае уравнение (2.82) |
также упрощается и |
||||||
принимает вид |
|
|
|
|
|
|
|
P(x, y) |
d |
|
Q |
|
P |
|
|
|
|
|
|
|
. |
(2.88) |
|
|
|
|
|||||
|
dy |
|
x |
|
|
|
|
|
|
|
y |
|
|||
Если P(x, y) 0, имеем:
d (y) |
|
1 |
|
Q(x, y) |
|
P(x, y) |
|
|
|
|
|
dy. |
|||||
|
|
|
|
|||||
(y) |
|
|
x |
|
y |
|
||
P(x, y) |
|
|
||||||
Если
1 |
|
|
Q(x, y) |
|
P(x, y) |
|
(2.89) |
|
|
|
|
(y), |
|||||
|
|
|
|
|
||||
|
|
|
|
x |
|
y |
|
|
|
P(x, y) |
|
|
|
||||
то, интегрирующий множитель дается формулой |
|
|||||||
|
|
(y) exp( (y)dy). |
(2.90) |
|||||
При этом условие (2.89) является необходимым и достаточным для того, чтобы уравнение (2.78) имело такой интегрирующий множитель.
Имеется, помимо рассмотренных, немногочисленные случаи, для которых
интегрирующий множитель находится без затруднений. |
Например, легко |
|
находится интегрирующий множитель |
уравнения с |
разделяющимися |
52 |
|
|
переменными, однородного дифференциального уравнения 1-го порядка и в некоторых других случаях, на которых мы не будем останавливаться.
Рассмотрим примеры интегрирования конкретных дифференциальных уравнений с помощью интегрирующего множителя.
Пример. Найти общий интеграл уравнения
(3x 6xy 3y2)dx (2x2 3xy)dy 0.
Решение. Это дифференциальное уравнение не является ни уравнением с разделяющимися переменными, ни однородным, ни линейным, ни уравнением Бернулли. Выясним, является ли оно уравнением в полных дифференциалах.
Проверим выполнение условия |
P |
|
Q |
: |
|
|
|
|
||||
|
|
|
|
|
|
|||||||
|
P(x, y) |
|
|
|
y |
x |
Q(x, y) |
|
|
|
||
|
|
(3x 6xy 3y2) 6x 6y; |
|
|
(2x2 3xy) 4x 3y. |
|||||||
|
y |
|
x |
|
||||||||
|
|
y |
|
|
|
x |
||||||
Видим, что условие не выполняется. Проверим, имеет ли уравнение интегрирующий множитель, зависящий только от x, воспользовавшись условием (2.85). Имеем:
1 |
P(x,y) |
Q(x, y) |
1 |
|
1 |
|||||
|
|
|
|
|
|
|
|
(2x 3y) |
|
(x). |
|
|
|
|
|
||||||
|
|
y |
x |
|
|
x(2x 3y) |
|
x |
||
Q(x, y) |
|
|
|
|||||||
Уравнение имеет интегрирующий множитель, зависящий от x, который находим по формуле (2.87):
|
|
dx |
|
ln x |
|
||
(x) exp |
|
|
e |
|
|
x. |
|
|
|
|
|||||
|
x |
x, |
|
|
|||
Умножив обе части уравнения |
на |
получим уравнение в полных |
|||||
дифференциалах:
(3x2 6x2y 3xy2)dx (2x3 3x2y)dy 0.
Общий интеграл этого уравнения найдем по формуле (2.74), положив
x0 y0 |
0: |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
3 |
|
|
|
|
(3x2 6x2y 3xy2)dx C, x3 |
2x3y |
x |
2y2 C. |
||||||
|
2 |
|||||||||
|
0 |
1 |
|
1 |
|
|
|
|
||
Общий интеграл получен. Поскольку |
|
0, |
то решения, не |
|||||||
|
|
x |
||||||||
|
|
|
|
|
|
|
|
|||
вытекающего из общего нет. Решение x 0, входящее в состав общего интеграла (при C 0), не является посторонним, что показывает его подстановка в исходное уравнение.
Пример. Найти общий интеграл уравнения y(1 xy)dx xdy 0. Решение. Это уравнение является уравнением Бернулли, но мы построим
решение, приведя его к виду уравнения в полных дифференциалах.
53
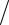
P(x, y) |
|
|
(y xy2) 1 2xy; |
Q(x, y) |
1; |
|||||||||
|
y |
|
||||||||||||
|
|
|
||||||||||||
|
|
|
y |
|
|
|
|
|
x |
|||||
1 |
|
P(x,y) |
Q(x,y) |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2 2xy) (x). |
||
|
|
|
|
|
|
|
|
|||||||
|
Q(x,y) |
|
y |
x |
|
|
x |
|
|
|||||
|
|
|
|
|
|
|||||||||
Таким образом, уравнение не имеет интегрирующего множителя, зависящего только от x. Проверим выполнение условия (2.89):
|
|
|
1 |
|
|
|
|
|
|
|
|
|
P(x,y) |
|
|
|
|
2(1 xy) |
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
Q(x, y) |
|
|
|
|
|
(y). |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
y(1 xy) |
|
|
y |
|||||||||||||||||
|
|
|
|
P(x, y) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Уравнение имеет интегрирующий множитель, зависящий от y. Находим |
||||||||||||||||||||||||||||||||||||
его по формуле (2.90): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
2ln y |
1 |
|
|||||||
|
|
|
|
(y) exp( |
(y)dy) exp |
2 |
|
|
|
e |
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Умножив, данное уравнение на 1 y2 , превращаем его в уравнение в |
||||||||||||||||||||||||||||||||||||
полных дифференциалах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
dx |
|
dy 0. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Его общий интеграл найдем по формуле (2.74), полагая x0 0, y0 1. |
||||||||||||||||||||||||||||||||||||
Имеем: |
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x dx |
0dy C, |
|
|
|
|
|
|
|
|
|
|
C. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Кроме общего интеграла получаем дополнительное решение, не |
||||||||||||||||||||||||||||||||||||
вытекающее |
|
из |
общего, |
из |
|
уравнения |
|
|
|
1 |
y2 0, y 0. Поскольку |
||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
0, |
то в общем интеграле не содержится посторонних решений. |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для некоторых уравнений удается найти интегрирующий множитель подбором. В этом случае бывает полезным следующее утверждение.
Теорема. Если (x, y) - интегрирующий множитель уравнения (2.78), т.е. (x,y)P(x,y)dx (x,y)Q(x,y)dy dU(x,y), то интегрирующим множителем является функция (U) , где (z)- произвольная непрерывная функция, не равная нулю.
Доказательство. Пусть F(z) - первообразная для функции (z), т.е. F (z) (z). Тогда имеем:
(U) Pdx Qdy (U)dU F (U)dU dF(U).
54
Это и доказывает, что (U) - интегрирующий множитель уравнения
(2.78).
Задачи для самостоятельного решения
Найти интегрирующий множитель и проинтегрировать уравнения:
1. |
(x2 y2 |
2x)dx 2ydy 0. |
|
Ответ: ex; |
ex(x2 y2) C. |
|
|
|
||||||||||||||||||||||||||
2. |
|
dy |
(3x2 cos y sin y)cos y. |
Ответ: |
1 |
|
|
; |
|
x(x2 tg y) C; |
y |
|
k . |
|||||||||||||||||||||
|
dx |
|
||||||||||||||||||||||||||||||||
|
cos2 |
y |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
(x |
2 |
|
|
|
2 |
y)dx xsin2ydy 0. |
|
1 |
|
; |
x |
2 |
sin |
2 |
y Cx. |
|
|
|
|||||||||||||||
3. |
|
sin |
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y2 |
x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4. |
1 |
|
dx 2xy |
|
|
|
|
dy 0. |
Ответ: |
|
; |
ln |
x |
ln |
y |
|
|
C. |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
y |
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.8.Пфаффовы формы, полный дифференциал и термодинамика
1.Дифференциальные соотношения, используемые в термодинамике, такие как уравнение первого закона термодинамики для простых систем
Q dU A, |
(2.91) |
где, Q - количества тепла подводимого (или отводимого) к рассматриваемой термодинамической системе; U - внутренняя энергия системы; A - работа, производимая системой (или производимая над системой);
соотношение для работы термодинамической системы, связанной с увеличением объема V системы против сил внешнего давления p
A pdV; |
(2.92) |
уравнение второго закона термодинамики |
|
Q TdS, |
(2.93) |
где, S и T - энтропия и температура системы;
объединенное уравнение первого и второго законов термодинамики (для простой системы)
TdS dU pdV;
а также ряд других термодинамических соотношений, сходны между собой по структуре и имеют следующий вид
Z A1(x1, ,xn)dx1 An(x1, ,xn)dxn,
где x1, ,xn - независимые переменные.
Выражение вида
n |
|
đZ Ak (x1, ,xn)dxk |
(2.94) |
k 1 |
|
55

называется дифференциальным выражением Пфаффа или пфаффовой формой.
(Пфафф Иоганн Фридрих 1765-1825 г.г. – немецкий математик и астроном, один из учителей К. Гаусса. Наибольшие достижения Пфаффа относятся к области исследования теории важного класса дифференциальных уравнений). В формуле (2.94) перечеркнутая буква đ означает, что в правой части равенства стоит, вообще говоря, дифференциальное выражение, которое может быть и полным дифференциалом. Таким образом, введенный символ “đ” объединяет две возможности: đ d , когда правая часть этого равенства
представляет собой полный дифференциал; đ |
- в том случае, когда правая |
|
часть не является полным дифференциалом. |
|
|
Сравнивая, |
например, уравнение первого закона термодинамики для |
|
простых систем |
(2.91) с выражением (2.94) |
видим, что первый закон |
термодинамики представляет собой пфаффову форму двух переменных; для термодинамических систем, совершающих, помимо работы расширения, еще один вид работы - пфаффову форму трех переменных
Q dU pdV W ,
где - любая обобщенная сила, за исключением давления, W - любая обобщенная координата, за исключением объема. Выражения (2.92) и (2.93) очевидно являются пфаффовыми формами одного переменного.
2. При рассмотрении дифференциальных выражений вида (2.94) важнейшим вопросом для теории дифференциальных уравнений является вопрос о том, будет ли это выражение полным дифференциалом. Этот вопрос в частном случае двух переменных мы изучали в п. 2.6 и п. 2.7.
Различие в поведении пфаффовых форм, представляющих собой полный дифференциал
|
n |
|
|
|
|
n Z(x , ,x |
n |
) |
|
|
dZ |
|
A (x , ,x )dx |
|
|
|
1 |
|
dx , |
||
|
xk |
|
|
|||||||
|
k 1 |
n |
k |
|
|
|
k |
|||
|
k 1 |
|
k 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
Ak (x1, ,xn) Z(x1,xk ,xn) ,
от пфаффовых форм, не являющихся таковыми, весьма существенна и для термодинамики. Дело в том, что вычисленный по любой линии, соединяющий точки M1 и M2 , интеграл от полных дифференциалов
dZ Z(M2) Z(M1) |
(2.95) |
|
M1M2
равен разности значений функции Z в этих точках (не зависит от вида линии). Если же đZ dZ, то величина интеграла зависит не только от координат точек M1 и M2 , но и от вида кривой, соединяющей эти точки:
56

|
|
|
đ Z Z(M1M2). |
(2.96) |
M1M2
В термодинамике при отсутствии внешних воздействий на простую однокомпонентную систему ее состояние определяется заданием двух независимых интенсивных параметров (Напомним: термодинамические параметры, не зависящие от массы или числа частиц в системе, называются интенсивными). Любой другой параметр состояния такой системы является функцией двух заданных параметров. Иными словами – любые три параметра состояния (например, давление p, удельный объем v V m или температура T ) однозначно связаны между собой. Уравнение, связывающее эти параметры,
m или температура T ) однозначно связаны между собой. Уравнение, связывающее эти параметры,
называется уравнением состояния вещества.
Например, уравнения состояния идеального газа – уравнение Клапейрона - Менделеева, имеет вид: pV vRT , где v m - число молей газа; m - масса
- число молей газа; m - масса
газа; - молярная масса; |
R 8314,4 Дж (киломоль.K) - универсальная |
(молярная) газовая постоянная.
Всистеме координат, по осям которой отложены величины этих параметров, связь между параметрами состояния представляется в виде поверхности состояния. Изменение состояние термодинамической системы приводит к перемещению по поверхности состояния изображающей состояние точки; кривые на поверхности состояния – траектории этой точки.
Втермодинамике разделяют все термодинамические функции на два вида
–функции состояния и функции процесса. Первые из них характеризуются тем,
что при малом изменении состоянии системы изменение этой функции является полным дифференциалом, т.е. при конечном перемещении точки, изображающей состояние системы, имеет место формула (2.95). Для функций процесса – имеет место формула (2.96).
Вп. 2.6 и п. 2.7 мы рассмотрели два класса пфаффовых форм, зависящих от двух переменных: пфаффовы формы, которые не являются полным дифференциалом, но имеют интегрирующий множитель, умножение на который превращает дифференциальное выражение в полный дифференциал некоторой функции.
Например, второй закон термодинамики в формулировке Р. Клаузиуса (Рудольф Юлиус Эмануэль Клаузиус 1822 - 1888 г.г. – выдающийся немецкий
физик) вводит понятие энтропии соотношением dS |
1 |
Q. Энтропия, в |
|
||
|
T |
|
отличии от количества тепла, является функцией состояния и потому dS - есть
полный дифференциал. Последнее означает, что 1 является интегрирующим
T
множителем для пфаффовой формы đQ Q.
57

Кроме указанных выше классов, существует третий класс пфаффовых форм. Принадлежащие этому классу дифференциальные выражения не являются полными дифференциалами, и не имеют интегрирующего множителя.
Голономными пфаффовыми формами называются такие линейные дифференциальные формы (2.94), которые имеют интегрирующий множитель (очевидно, что формы 1-го класса – частный случай 2-го класса).
Пфаффовы формы третьего класса (не имеющие интегрирующего множителя) называются неголономными.
Доказано, что пфаффовы формы двух переменных всегда голономны. В случае трех и более переменных можно утверждать, что одни из них голономны, другие - неголономны. В частности, линейная дифференциальная форма трех переменных
P(x, y,z)dx Q(x, y,z)dy R(x, y,x)dz
голономна в том случае, если выполняется соотношение:
|
Q |
|
R |
|
|
R |
|
||||
|
|
|
|
|
|||||||
P |
|
|
|
|
|
|
|
Q |
|
|
|
z |
|
y |
|
|
|||||||
|
|
|
|
|
|
x |
|
||||
|
x,y |
|
|
|
|
|
|
y,z |
|||
|
|
|
|
|
|
x,z |
|
|
|
||
Qz x,y
|
|
|
|
|
|
Q |
|
|
|
P |
|
|
|||||
|
R |
|
|
|
|
|
|
0. |
|
|
|
||||||
|
|
|
|
|
|
x |
|
|
|
y |
x,z |
||||||
|
|
|
|
|
|
|
y,z |
|
Приведенный в этом параграфе материал указывает перспективу развития теории, изложенной в п. 2.6 и п. 2.7 и связь формальной математической теории с физикой тепловых процессов. В третьем семестре курса “Высшая математика” мы покажем связь этой теории с теорией потенциала, имеющей важнейшее значение для гидро- и аэродинамики, термодинамики и теории электричества.
2.9.Применение дифференциальных уравнений первого порядка
кзадачам физики и экологии
З а д а ч а о р а д и о а к т и в н о м р а с п а д е. Экспериментальным путем установлено, что скорость распада радиоактивного вещества, т. е. скорость изменения его массы в зависимости от времени, прямо
пропорциональна его количеству. Установим закон |
изменения |
|
массы m |
||||||||||
радиоактивного вещества в зависимости от времени |
t , |
считая, |
что начальная |
||||||||||
масса вещества при t 0 |
была |
m0. |
|
|
m, в момент времени |
||||||||
Пусть в момент времени |
t масса вещества есть |
||||||||||||
t t масса составляет |
m m. За время |
t |
распадается |
масса |
m. |
||||||||
Отношение |
m |
средняя скорость распада за время |
t, a |
lim |
|
m |
|
dm |
|
||||
|
|
|
|
||||||||||
|
t |
|
|
|
|
t 0 t |
dt |
||||||
мгновенная скорость распада в момент времени |
t . |
|
|
|
|
|
|
|
|
||||
58

Согласно условию
dm |
km, |
(2.97) |
|
||
dt |
|
|
где k коэффициент пропорциональности (знак минус взят потому, что масса вещества убывает с течением времени, а производная убывающей функции отрицательна). Получено дифференциальное уравнение первого порядка, из которого надо найти зависимость массы m от времени t . Решая уравнение,
находим dm kdt, lnm kt lnC, откуда
m |
|
m Ce kt. |
(2.98) |
Формула (2.98) дает зависимость массы вещества как функции времени. В данной задаче постоянная C имеет определенное значение, а именно: при t 0
получаем m0 Ce0 C. Подставляя это значение C в формулу (2.98), получаем
искомую зависимость массы радиоактивного вещества от времени: |
|
m m0 e kt. |
(2.99) |
Равенство (2.98) представляет собой общее решение дифференциального уравнения, а равенство (2.99) частное решение, отвечающее начальному условию данной задачи.
Коэффициент k определяется экспериментально. Например, для радия k 0,000447. Промежуток времени T , за который распадается половина первоначальной массы радиоактивного вещества, называют периодом полураспада этого вещества. Подставляя в формулу (2.99) вместо m значение m0 /2, вместо k значение 0,000447, получаем уравнение для определения периода полураспада T радия:
|
|
|
m0 |
m e 0,000447T |
, 0,000447T ln2, |
|
|
|
|
|
|
||
|
|
2 |
0 |
|
||
|
ln2 |
|
|
|||
откуда T |
|
|
;T 1550 лет. |
|
||
|
|
|
|
|||
0,000447 |
|
|
||||
З а д а ч а |
о з а к о н е «е с т е с т в е н н о г о р о с т а1». Закон |
|||||
«естественного роста» это закон, согласно которому скорость «роста» вещества прямо пропорциональна его количеству. Найдем формулу для определения изменения количества вещества y в зависимости от времени t , считая, что в начальный момент t 0 количество вещества было равно y0 .
Здесь независимой переменной является время t , а искомой величиной количество вещества в любой момент времени. Скорость «роста» вещества есть скорость изменения величины y в зависимости от переменной t .
___________________________________________________________________
1Примеры заимствованы из книги проф. МГУ Ризниченко Г.Ю. Лекции по математическим моделям в биологии. Ч.1. – Ижевск: НИЦ “Регулярная и хаотичная динамика”, 2002. 232 с.
59
