Учебное пособие 800446

Задачи для самостоятельного решения

Решить уравнения:

1.y 5y 4y 0. Ответ: y C1ex C2e4x.

2.y 6y 9y 0. Ответ: y e3x(C1 C2x).

3.y 8y 25y 0. Ответ: y e 4x (C1 cos3x C2 sin x).

4.y 3y 2y 0. Ответ: y C1ex C2e2x.

5.y 4y 4y 0. Ответ: y e2x C1 C2x .

6.y 2y 2y 0. Ответ: y ex(C1 cos x C2 sin x).

7.y 4y 3y 0. Ответ: y C1ex C2e3x.

8.y 4y 0. Ответ: y C1e2x C2e 2x.

9.y 4y 0. Ответ: y C1 C2e 4x.

10.y 3y 2y 0. Ответ: y C1e 2x C2e x.

11.y 2ay a2y 0. Ответ: y (C1x C2)e ax.

12.y 2y 5y 0. Ответ: y e x(C1 cos2x C 2 sin2x)

13.y y 0. Ответ: y C1ex C2e x.

14.y y 0. Ответ: y C1cosx C2 sin x.

19.y 2y xe x. Ответ: y C1ex2 C2e x2 (x 2)e x.

20.y 4y 8x3. Ответ: y C1e2x C2e 2x 2x3 3x.

5. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

5.1.Нормальные системы дифференциальных уравнений

1.Понятие о нормальной системе. Линейные системы. Автономные системы

Нормальная система обыкновенных дифференциальных уравнений содержит n неизвестных функций одного переменного и состоит из n уравнений первого порядка, каждое из которых содержит производную только одной из функций и разрешено относительно этой производной:

dyn fn(x,y1,y2, ,yn);dx

где y1, y2,..., yn - искомые функции от независимой переменной x, f1,..., fn -

заданные функции, зависящие от (n 1) переменных. Число уравнений, входящих в систему (5.1), называется порядком этой системы. То есть, согласно этому определению, система (5.1) есть система n- го порядка.

К нормальному виду может быть приведена система уравнений высших порядков, каждое из которых разрешено относительно старшей производной. Для этого должны быть введены дополнительные функции, как в рассмотренном ниже примере.

Fимеет вид:

dt,rt,

Подставив разложения r и F в уравнение (5.2), приравняв проекции на координатные оси. Получим систему трех уравнений:

где точка над буквой обозначает производную по t. Каждое из уравнений системы (5.3) является дифференциальным уравнением второго порядка. Для

Подобным образом и одному дифференциальному уравнению высшего порядка можно сопоставить систему дифференциальных уравнений первого порядка.

Система уравнений (5.1) называется линейной системой дифференциальных уравнений, если правые части зависят линейно от некоторых функций y1, y2, , yn :

113

имеет решение y1 ex, z1 ex. В этом можно убедиться, подставив эти функции в уравнения системы:

ex 7ex 6ex, ex 6ex 7ex.

Мы получили тождества, справедливые при x ( ; ) . Эта же система имеет и другие решения. Например, решением, является другая совокупность

любых числовых значениях параметров A и B.

Рассмотренный пример системы двух уравнений наводит на мысль, что всякая система двух уравнений имеет решение, содержащее два произвольных параметра.

совпадает с направлением поля в этой точке. Аналогичную геометрическую интерпретацию можно дать и нормальной системе n дифференциальных уравнений (5.1).

Будем рассматривать (x,y1, , yn) как координаты точки в (n 1)- мерном пространстве x, y1, , yn. Тогда решению y 1(x), y 2(x), , y n(x)

fn(x, y1, y2, , yn) в системе (5.1) определены и конечны в некоторой области

Если в точке M0(x0, y1(x0), , yn(x0)) все правые части системы (5.1)

или некоторые из них обращаются в неопределенные выражения вида

то в этой точке поле направлений не определено и через такую точку не проходит ни одна интегральная кривая.

Рассмотрим механическое истолкование нормальной системы.

Если дифференциальные уравнения описывают движение механической системы, то независимую переменную обозначают t, искомые функции через

движения или движение по некоторой траектории с течением времени t. Если

векторном уравнении (5.7) не зависят от времени t, то система (5.6), или (5.7),

называется автономной динамической системой.

Взаимосвязь между траекторией и движением состоит в том, что

уравнения траектории движения (в пространстве x1,x2,...,xn ). Эти уравнению определяют траекторию как однопараметрическое геометрическое место точек; они показывают, как происходит движение точки по траектории с течением времени. В соответствии с этим решение системы x1 1(t),x2 2(t), ,xn n(t) обычно в механике называют движением.

Основной задачей интегрирования системы (5.6) или (5.7) является нахождение всех движений, определяемых этой системой и изучение свойств движений.

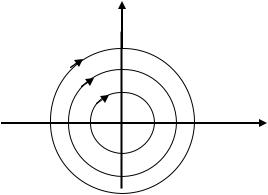
Пример. Пусть задана система уравнений x y, y x. Можно убедиться непосредственной подстановкой в уравнения, что семейство

точки по определенной траектории в направлении, показанном на рис. 11.

y

s1 s2

x

Рис. 11. Фазовые траектории системы

Отметим, что уравнение траектории на фазовой плоскости не зависит от C2 . Поэтому все движения при фиксированном C1 происходят по одной и той

же траектории. При C1 0 (x2 y2 0) фазовая траектория состоит из одной точки (точки О), называемой в этом случае точкой покоя системы.

5.2.Задача Коши. Достаточные условия существования

иединственности решения задачи Коши. Общее, частное

иособое решения

1.Задача Коши для системы вида (5.1) ставится так: среди всех решений

системы найти такое решение y1 1(x), , yn n(x), в котором функцииk (x) (k 1,2, ,n) принимают заданные числовые значения y1(0), y2(0), , yn(0)

при заданном числовом значении x x0 независимой переменной:

117

1(x0) y1(0), , n(x0) yn(0).

Совокупность чисел x0, y1(0), , yn(0) называется начальными данными решения y1 1(x), , yn n(x); число x0 называют начальным значением

независимой переменной; числа y1(0), , yn(0) называются начальными

значениями искомых функций (начальные значения решения). Геометрический смысл задачи Коши заключается в том, что среди всех

интегральных кривых системы разыскивается та, которая проходит через