1.2.1. Фермионы

Функция распределения Ферми-Дирака имеет вид

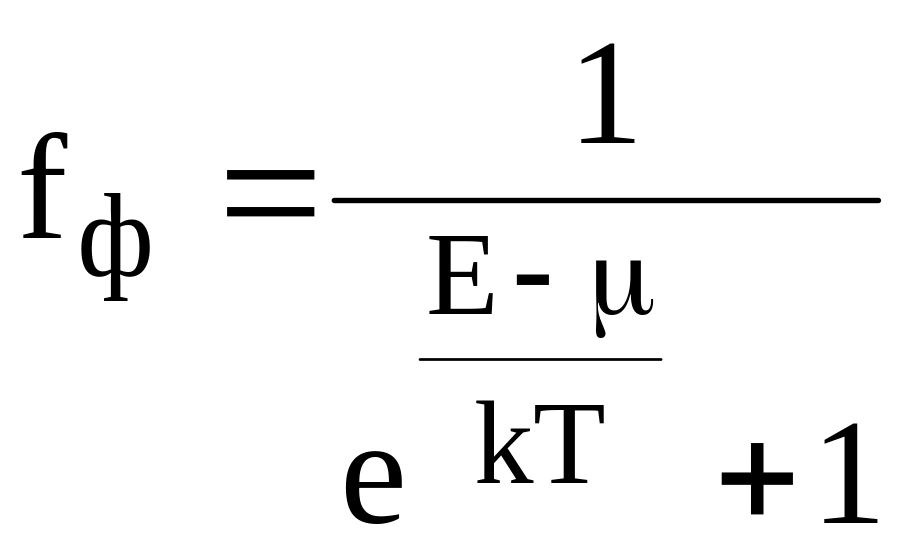. (1.9)

Если умножить f(E) на число состояний g(E)dE, приходящихся на интервал dE, где g(Е) - плотность состояний, то найдем закон распределения фермионов по энергиям

, (1.10)

где (2S+1) - число состояний спина (S) частицы (спиновые состояния); V- объем слоя сферы в пространстве Е (см. рис.1.1); - число фазовых ячеек в этом слое. Кроме того, необходимо помнить, что .

Умножив обе части уравнения (1.10) на получим его в виде

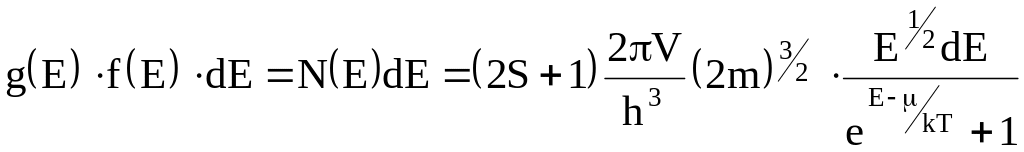. (1.11)

Т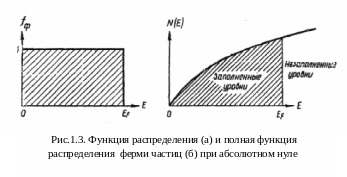 ак как для электронов , тогда окончательно запишем выражение для полной функции распределения .

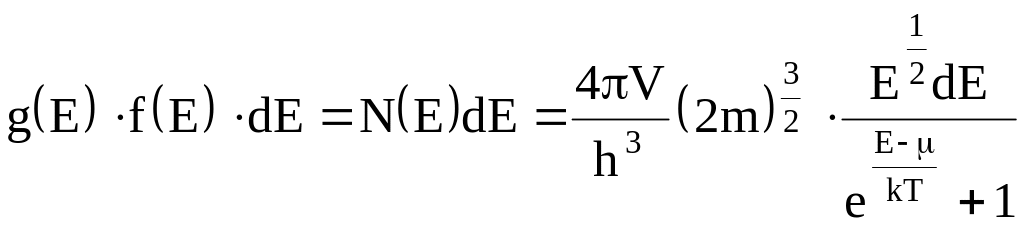. (1.12)

Функция распределения Ферми частиц (рис.1.3, а) и их полная функция распределения (рис.1.3, б) показаны в отсутствии тепловых колебаний, т.е. при Т = 0. Так как электроны подчиняются принципу Паули, они не скапливаются на дне потенциальной ямы (см. рис. 1.4), а последовательно занимают попарно все уровни вплоть до уровня Ферми и при Т= 0, Е_max = Е_F называется энергией Ферми (рис.1.4).

Вероятность заполнения электронами состояний при Т= 0 с энергией меньше E_F равна единице (на рис.1.3,а) видна резкая ступенька), а состояний с большим значением Е, чем E_F равно нулю. Это свойство можно записать:

(1.13)

Тот же результат можно получить из (1.9), для этого необходимо отсчитывать от дна ямы и тогда .

В этом случае (1.9) перепишем

. (1.14)

О ткуда следует, что если Е < E_F, то при Т=0, сомножитель а если Е > E_F, при Т = 0 величина и, естественно, f_Ф (Е) = 0. Для полной функции распределения (1.10) при Т= 0 можно записать с учетом (1.12) следующее выражение

.

Что графически показано на рис. 1.3, б.

Энергия Ферми вычисляется из условия нормировки полной функции Ферми-Дирака при Т= 0, и в конечном счете записывается

, (1.15)

где n- число электронов в единице объема

при Т>Т_F выполняется критерий невырожденности.

Влияние температуры на уровень Ферми. Температурную зависимость Е_F можно получить из условия нормировки полной функции распределения Ферми-Дирака.

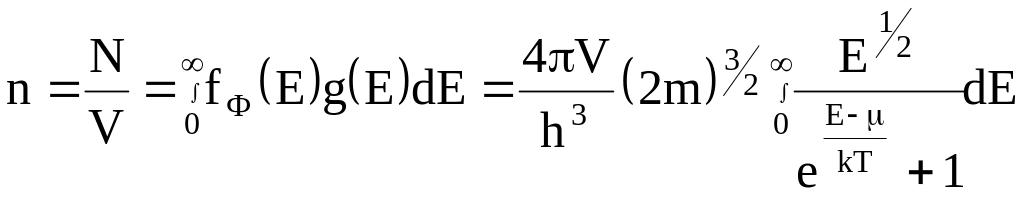. (1.16)

Интеграл в правой части в явном виде не вычисляется.

Приближенное его вычисление для области низких температур (Т<<Т_F) дает

, (1.17)

для Т>Т_F выражение f_F (1.9) переходит в выражение (1.3) для классического газа.

Если в функции Ферми-Дирака положить , тогда и функция не зависит от Т, т.е. равна 1/2. Это дает возможность определить характер изменения f_Ф от температуры, как показано на рис.1.5.

Видно, что если с повышением температуры уровень Ферми смещается по оси энергии влево, то влево смещаются и точки А. При Т>Т_F функция Ферми - Дирака переходит в функцию Максвелла - Больцмана и становится отрицательной (точка A₄).

1.2.2 Бозоны

Функция распределения их впервые была получена Бозе и Эйнштейном в виде

. (1.18)

Как и для ферми-газа бозе - газ также имеет некоторую характерную температуру То - температуру вырождения. Она хотя и несколько отличается от То ферми-газа, но имеет с ней одинаковый порядок

.

При температурах О <Т<<Т₀ почти все частицы имеют импульс равный нулю и только их небольшое количество имеет импульс отличный от нуля, т.е. движется. Однако при Т=Т_Б = 3,31 Т₀ движутся все частицы. Символом Т_Б обозначена температура вырождения идеального газа бозонов, т.е. частиц с целочисленным спином, в том числе равным нулю. Число бозонов не сохраняется, и оно зависит от температуры. При Т<< То, как мы отмечали, их число мало и корреляция между их движением не существенна. При температурах близких к температуре вырождения, их движения скоррелировано и поэтому движение каждой квазичастицы зависит от движения всех остальных. В качестве примеров поведения бозонов в литературе рассматриваются фононы, которые обладают рядом особенностей [2].