3.1. Теплоемкость твердого тела

Тепловая энергия твердого тела Е_реш складывается из энергии нормальных колебаний решетки. Число нормальных колебаний, приходящихся на спектральный участок равно , умножая его на среднюю энергию Е_нк нормального колебания (3.3), получим суммарную энергию нормальных колебаний

, (3.4)

где g () - плотность состояний.

Проинтегрировав это выражение по всему спектру нормальных колебаний от 0 до , получим энергию тепловых колебаний решетки твердого тела

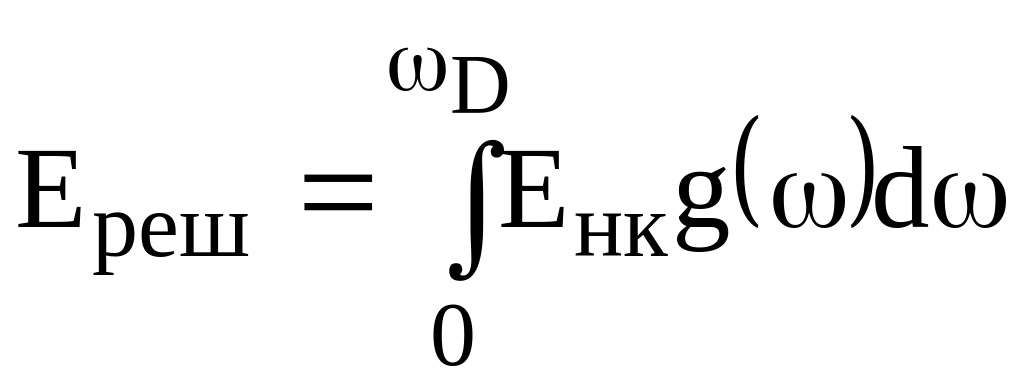. (3.5)

Теплоемкость твердого тела при постоянном объеме выражает изменение тепловой энергии при изменении температуры на 1 ⁰С. Это первая производная энергии по температуре, т.е.

(3.6)

в области высоких температур

,

где N_A - число Авогардо, N_A= , = R - универсальная газовая постоянная

. (3.7)

Рассмотрим температурную зависимость .

3.1.1. Область низких температур

В этой области возбуждаются в основном низкочастотные, нормальные колебания, кванты энергии которых . В этом случае приближенное значение средней энергии нормальных колебаний можно определить так: разлагаем знаменатель выражения (3.3) в ряд и ограничиваемся вторым членом разложения. Получим:

. (3.8)

Следовательно, в области низких температур средняя энергия каждого нормального колебания растет пропорционально абсолютной температуре

.

Кроме того, в этой области температур с повышением последней возбуждаются новые нормальные колебания с более высокими частотами. Их число ~ Т³.

В общую энергию вносят свой вклад оба фактора и тогда,

E_реш ~ T⁴,

а теплоемкость

. (3.9)

Это и есть закон Дебая. Графически зависимость представлена на рис.3.2.

Рис. 3.2. Температурная зависимость удельной теплоемкости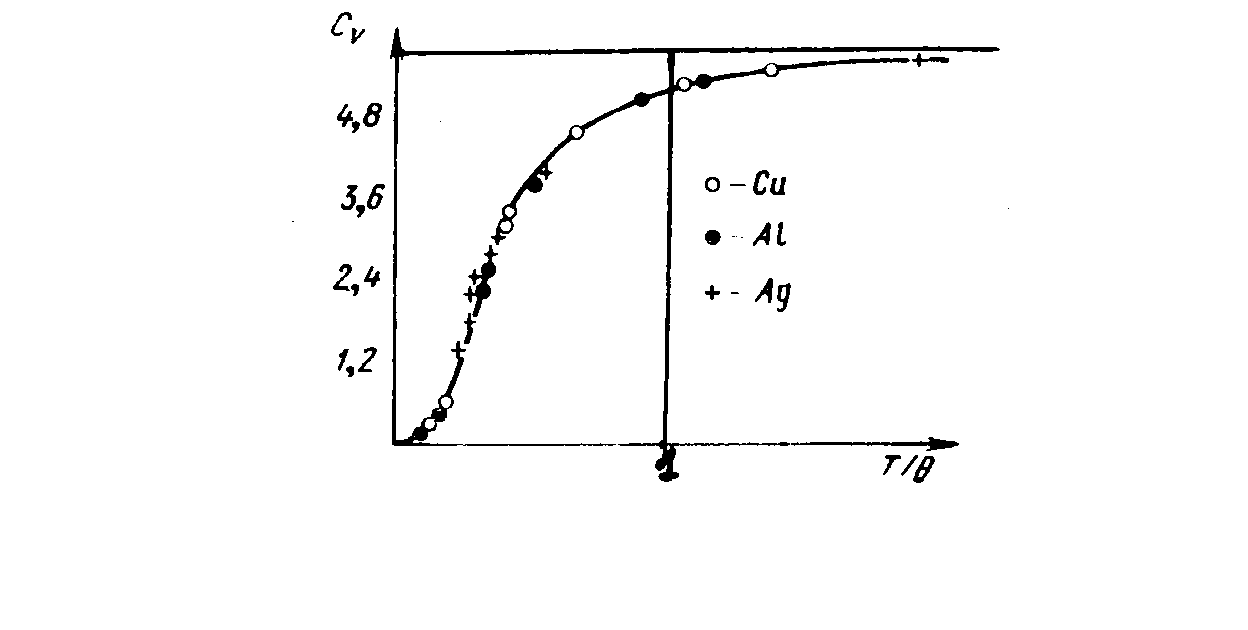

Теплоемкость электронного газа

В общем виде запишем, что теплоемкость имеет две составляющие: решеточную и электронную

.

Мы помним, что электронный газ является вырожденным и с повышением температуры растет число возбужденных электронов как показано на рис.1.5.

,

откуда с учетом заселения электронами разрешенных состояний

. (3.10)

Каждый электрон, подвергающийся термическому возбуждению, поглощает энергию порядка kT. Энергия, поглощенная всем возбужденным газом электронов, с учетом (3.10) равна

. (3.11)

Теплоемкость электронного газа равна

.

Более строгий расчет дает следующее выражение

. (3.12)

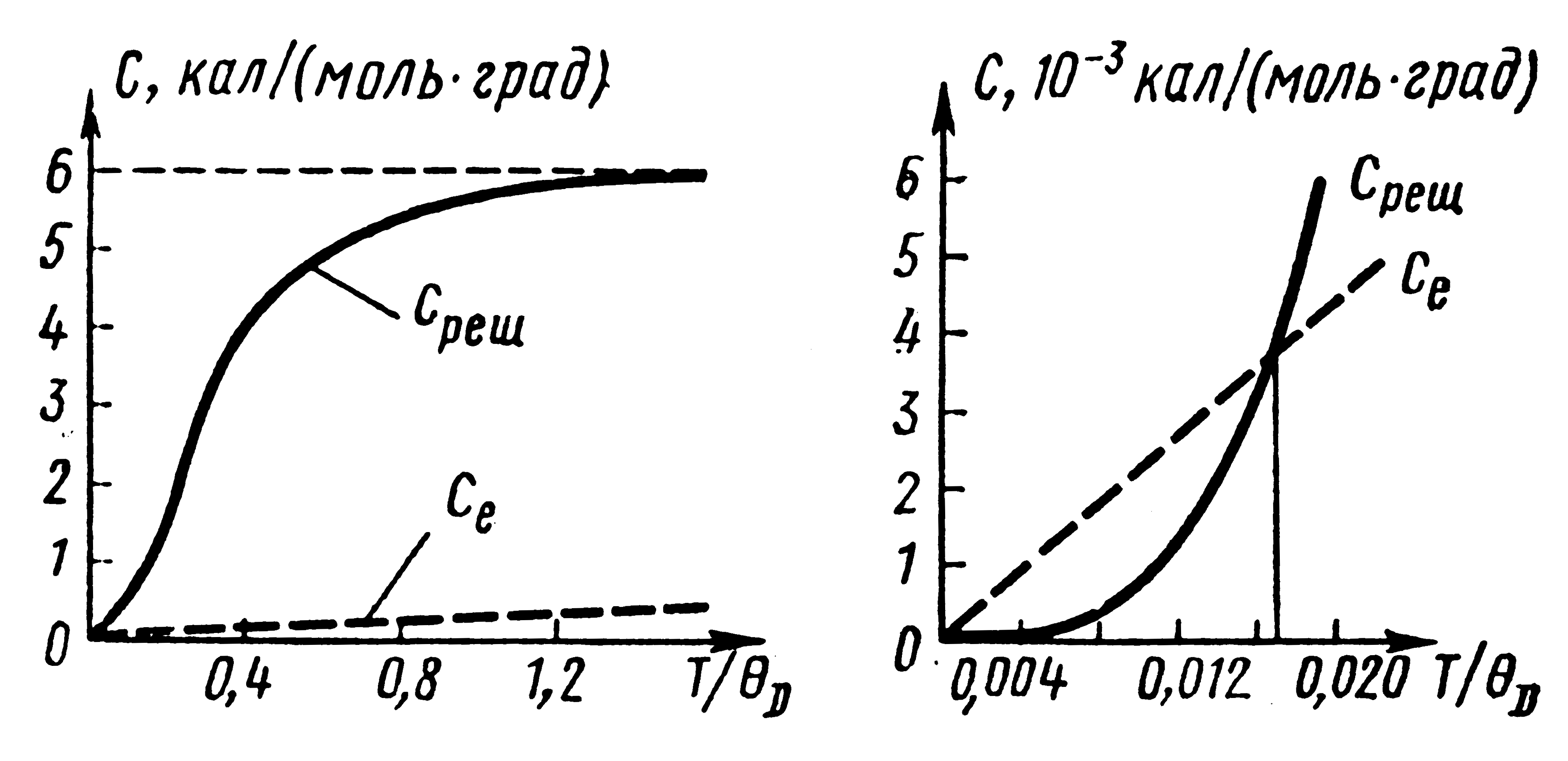
Рис. 3.3. Фононная и электронная составляющие удельной теплоемкости

В области же низких температур, где С_реш ~ Т, ее значение заметно уменьшается и вблизи абсолютного нуля С_реш. может оказаться столь малой, что основную долю удельной теплоемкости составляет теплоемкость электронного газа, как это хорошо видно из рис.3.3.

3.2. Тепловое расширение твердых тел

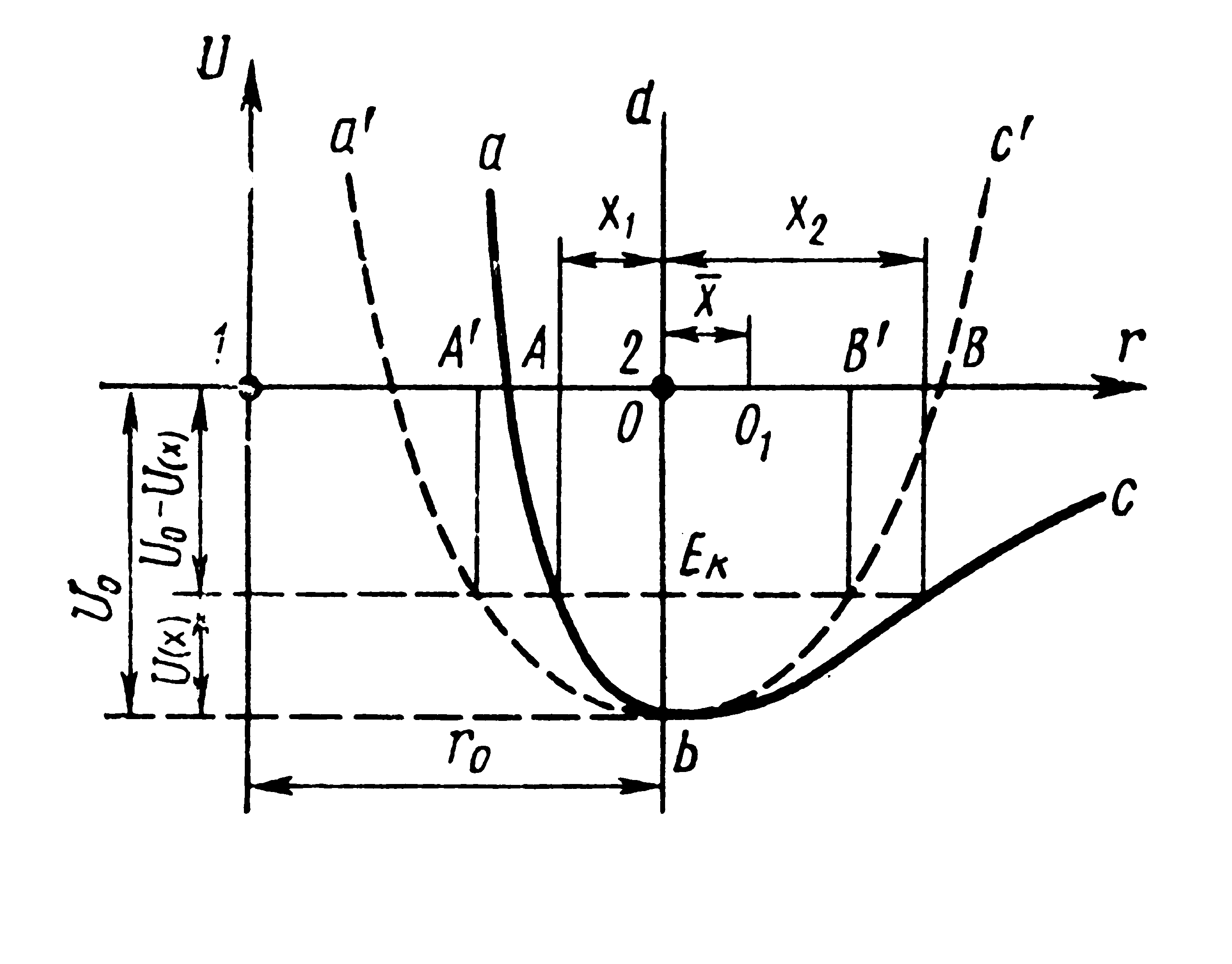
Для рассмотрения вопроса об изменениях объема твердого тела с температурой, возьмем систему из двух частиц (рис.3.4). Известно, что сила, возникающая при смещении частицы от положения равновесия пропорциональна смещению

,

а потенциальная энергия смещенной частицы пропорциональна квадрату смещения

. (3.13)

Рис. 3. 4 Схема взаимодействия атомов к вопросу расширения твердых тел

Из гармонического колебания частицы около положения равновесия (кривая ) следовал закон Гука. Однако с этой точки зрения оказалось невозможным объяснить такие параметры как тепловое расширение и теплопроводность. Рассмотрим зависимость потенциальной энергии взаимодействия частиц от расстояние между ними. Для этого будем считать, что в выбранной системе из двух частиц, которые находятся в точках 1 и 2 (рис.3.4.) частица 1 будет закреплена, а другая имеет возможность перемещаться относительно 1 под действием подводимого тепла.

Обозначим расстояние между частицами (период решетки) через r₀, а минимум энергии взаимодействия через U₀. Предположим, что Т>То, тогда частица 2 колеблется и естественно обладает некой наибольшей энергией U₀, которая при движении равна кинетической энергии U_k. Известно, что при колебаниях кинетическая энергия переходит в потенциальную и наоборот, т.е. , где U_n -потенциальная энергия частицы.

Если бы частица 2 совершала бы гармонические колебания ( ), то

тогда

(3.14)

и отклонения ее от положения равновесия были бы симметричны. Естественно, нагревание в этих условиях не приводило бы к расширению тела. В действительности же (закрепление также проведено в точке 1) из-за ангармоничности колебаний (кривая аbс) кривая энергии является несимметричной. Для учета асимметрии потенциальной кривой необходимо в уравнении (3.13) ввести дополнительный член - ( g- коэффициент пропорциональности), тогда (3.13) перепишем

; (3.15)

f (x) = - .

При отклонении частицы 2 вправо (Х>О) член вычитается, и ветвь bc идет пониже ветви bc'. При отклонении же влево (Х<0) член прибавляется к и ветвь ab идет круче ветви аb. Несимметричность кривой abc позволяет сделать вывод о том, что из-за ассиметричности в отклонении частицы 2 при тепловых колебаниях амплитуды оказываются неодинаковыми и, следовательно, среднее положение ее уже будет не точка 0, а 0', т.е. расстояние между частицами будет при некоторой температуре Т' > Т не r_о, а (r_о+Х).

Относительное линейное расширение представляет собой отношение измененного среднего расстояния Х между частицами к их нормальному расстоянию r_о.

Из уравнения (3.15) следует, что при отсутствии внешней силы осуществляются свободные колебания, т.е. при f(х) = 0

откуда

x = . (3.16)

При рассмотрении потенциальной энергии колеблющейся частицы с точностью до величины второго порядка малости из (3.15) для среднего значения имеем

(x) = ,

x²  ,

подставив это значение в (3.16) получим

= .

Учитывая полную энергию частицы Е = Е_к + Е_{n =} Е_к + (x) = 2 (x) перепишем

=

и ,наконец, относительное линейное расширение

.

Коэффициент линейного расширения

(3.17)

и окончательно имеем

,

где .

Из (3.17) видно, то коэффициент линейного расширения пропорционален удельной теплоемкости тела.