8.1. Изоэнтропное расширение

Для понижения температуры необходимо осущетвлять перенос тепла от тела с более низкой температурой, которое надо охладить к телу с более высокой температурой а для этого требуется совершить работу. Как следует из второго закона термодинамики понижение температуры системы сопряжено с изменением параметров ее состояния. Запишем выражение связывающее температуру с энтропией и параметром состояния в следующем виде

s = f (T, х) (8.4)

где х – параметр состояния, в разных системах он различен: для термодинамической системы, это давление, для магнитной – напряженность магнитного поля (Н), для электрических диполей – напряженность электрического поля (Е).

Для термодинамической системы, которая описывается выражением (8.4) является обязательным условием процесса охлаждения. Оно может служить основой для анализа самого процесса охлаждения. Графически зависимость (8.4) s -Т можно 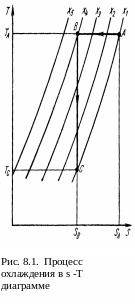представить, как показано на рис. 8.1. изотермическое сжатие (для термомеханической системы ). Отвод тепла . Затем, теплоизолируя систему, (изоэнтропный процесс), возвратим параметр s к исходному значению x, (процесс адиабатического расширение). Происходит качественное перераспределение энтропии и в результате температура падает.

Итак, только уменьшая энтропию, можно обеспечить понижение температуры, а для этого нужны некие физические методы.

Исходя из общего соотношения, связывающего температуру с энтропией и параметром состояния x, как записано в уравнении (8.4), и отождествляя х с давлением р x = p, запишем

. (8.5)

Дифференцируя (8.5) по Т и р получим

. (8.6)

Для рассматриваемого процесса ds = 0 и тогда из уравнения (8.6) получим

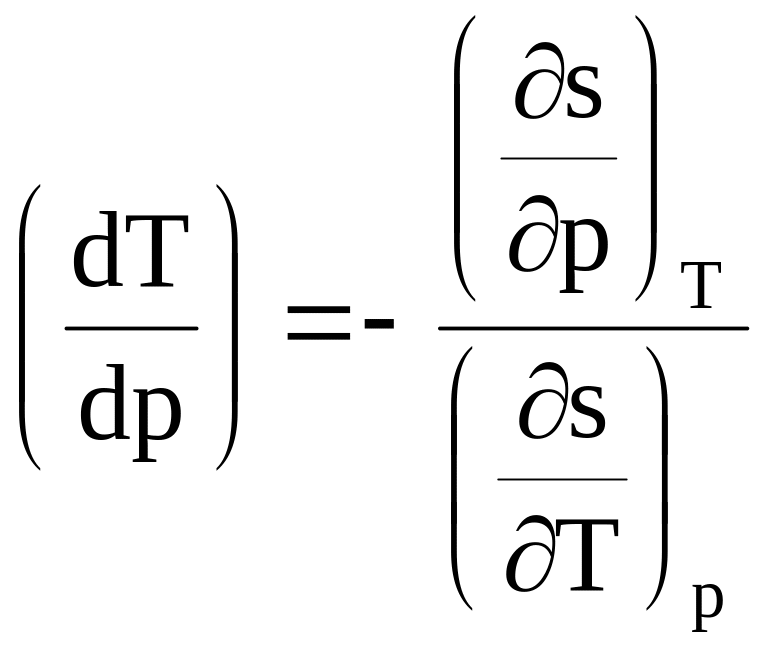(8.7)

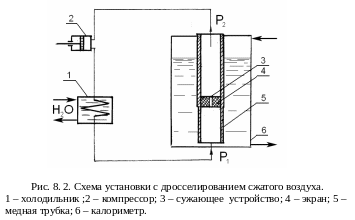
Для изобарного процесса

запишем

. (8.8)

Используя выражения термодинамического потенциала , дифференциал которого , запишем

, (8.9)

подставляя (8.9) и (8.8) в уравнение (8.7) получим

. (8.10)

Величина _s характеризует интенсивность охлаждения в процессе изоэнтропного расширения и называется дифференциальным эффектом процесса. Всегда больше нуля. Конечное изменение температуры в этом процессе может быть найдено с помощью s -T диаграммы ΔТ = Т_А-Т_с (рис. 8.1) или аналитически, интегрированием уравнения (8.9).

Осуществляется такой процесс в различного типа детандерах. Необходимо помнить, что в реальных условиях эксплуатации существует небольшая по величине необратимость, что и дает меньший эффект охлаждения. К.П.Д. процесса определяется как отношением величины понижения энтальпии газа от начальной i_н до конечной (i_к) точек, т.е. Δi = i_н – i_к к понижению энтальпии Δi_uд при идеальном обратимом расширении

 _о =

Величина _о зависит от типа детандера и условий его работы и обычно он составляет 0,85 ÷ 0,6..

8.2. Дросселирование сжатого газа

В основе этого процесса изменения температуры лежит эффект, обнаруженный Джоулем и Томсоном. Этот процесс протекает как без теплообмена, так и без совершения внешней работы. Он осуществляется при движении потока газа через сужающее устройство, где и происходит падение давления. Схема установки представлена на рис. 8.2. Компрессор 2 сжимает рабочий газ до давления р₁, который охлаждается в холодильнике 1 проточной водой. Далее газ поступает в калориметр 6 по медной трубке 5, где установлено сужающее устройство 3,изолированное экранами 4. В опытах Джоуля и Томсона сужающим устройством служила вата, а экраны изготовлялись из резины. С помощью термометров измеряли температуры на входе Т₁ и на выходе Т₂, а манометры позволяли определять перепад давления р = р₁- р₂ между входом газа и его выходом. Устанавливался ламинарный режим течения в местах, достаточно удаленных от сужающего устройства. Работа, связанная с продавливанием газа, рV определяет изменение внутренней энергии U до и после сужающего устройства (изменением кинетической энергии пренебрегаем)

или перепишем

,

т.е. энтальпии будут равными

i₁ = i₂ = const.

Определим дифференциальный эффект охлаждения (эффект Джоуля-Томсона) в этом процессе. Для этого используем

d _i = Тds + Vdp (8.11)

и подставляя значения для ds из (8.6) в (811) с учетом, что di=0, получим

,

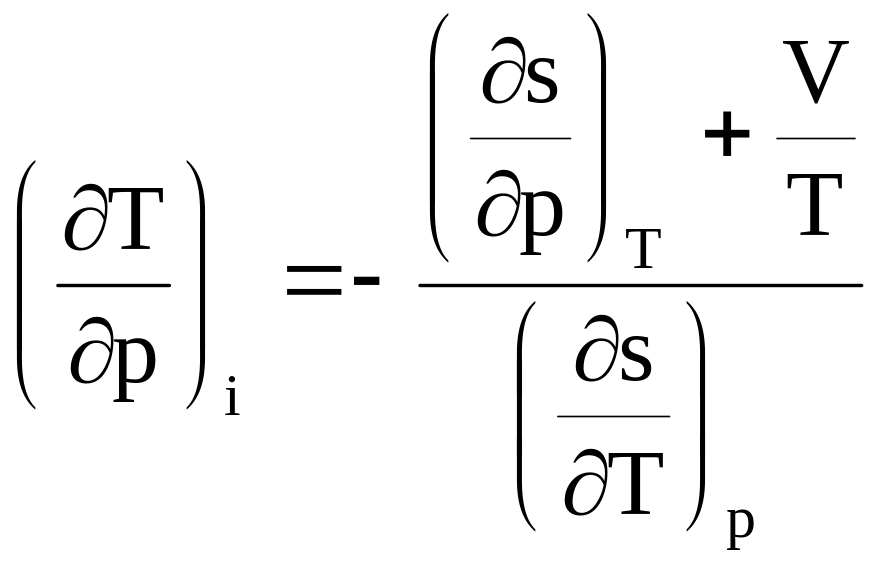используя выражения (8.8) и (8.9) окончательно получим

. (8.12)

Дифференциальный эффект Джоуля-Томсона ( ) также характеризует интенсивность изменения температуры. Это изменение температуры является следствием затраты работы на преодоление сил межмолекулярных внутренних связей.

Как следует из формулы (8.12) знак может быть как отрицательным, так и положительным, то есть – дросселирование может сопровождаться охлаждением или нагреванием рабочей среды. Изменение знака следует из условия =0

Из уравнения

рV = RT

получаем

.

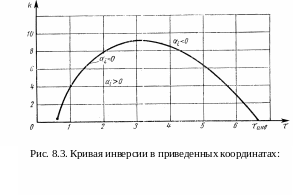
Кривая инверсии гелия (рис. 8.3) разграничивает области положительного и отрицательного эффектов Джоуля Томсона. При =0 существует температура инверсии выше которой всегда отрицательно и охлаждение получить невозможно. Все газы могут быть разделены на две группы: газы, у которых Т_инв>Т_среды и газы для которых, где Т_инв<Т_среды. У гелия Т_инв 40 К, а у водорода Т_инв = 204,6 К. При этом температура кипения жидкого водорода 20.4 К при атмосферном давлении и за счет уменьшения давления паров до 54 мм рт.ст может быть понижена до 14 К. При более низких давлениях, в отличии от гелия, водород переходит в твердую фазу (Т_к = 13,95 К).

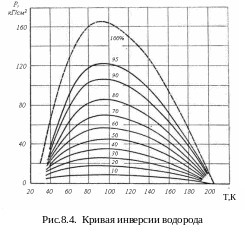
Кривая инверсии водорода показана на рис. 8.4. (пунктирной линией) в координатах абсолютное давление – температура. Сплошные линии соответствуют доле производительности в этом цикле по отношению к 100 %, взятым на кривой инверсии.

Наибольший эффект охлаждения при заданной температуре наблюдается при условии, если за начальное давление процесса принять давление, соответствующее точке на кривой =0, т.е. давление инверсии р = р_инв.

Тепловой эффект процесса характеризуется разностью энтальпий в точках, соответствующих начальному и конечному давлению при Т= const

. (8.13)

Эта величина называется изотермическим эффектом дросселирования.