
Методическое пособие 657
.pdf
В левом маркере этого оператора должно быть определено преобразуемое выражение без знака равенства, в правом – переменная, по которой осуществляется преобразование:
d 2 |
R d |
|
|
|
1 |
|
|
|
|
|
|||||||
|
i t |
|
|
|
|
|
i t |
|
|
|
|
i t laplace, t |
S (S |
laplace i t ,t, s |
|||
dt2 |
|
L |
dt |
|
|
L |
C |
||||||||||
|
|
t |
0 |
R |
(S |
laplace i t ,t, s |
i 0 ) |
|
1 |
laplace i t ,t, s |
|||||||
|
L |
|
L C |
||||||||||||||
i 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d |
i t |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||
Далее необходимо упростить это громоздкое выражение. Для этого переменную laplace i t ,t, s заменим на Z . Начальное условие для первой производной
|
t |
0 |
|
|
|
|
|
d |
i t |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
запишем в виде i 0 . |
|
|
|
|||
В результате получим выражение |
|
|
||||
S S Z i0 i 0 |
R |
S Z i0 |
1 |
Z. |
||
|
|
|||||
L |
L C |
|||||
После проведенных замен уравнение следует разрешить относительно переменной Z, т.е. использовать специальный оператор символьного решения уравнений solve панели Symbolic
(Символьные) и принять, что i0 0 , а i 0 |
E |
. |
|
||
|
L |
|
При таких начальных условиях после применения оператора solve получаем, что
S S Z |
E |
|
R |
S Z |
1 |
Z solve, Z |
E |
C. |
|
|
|
|
|
||||
L |
|
L |
L C |
S 2 LC rSC 1 |
61
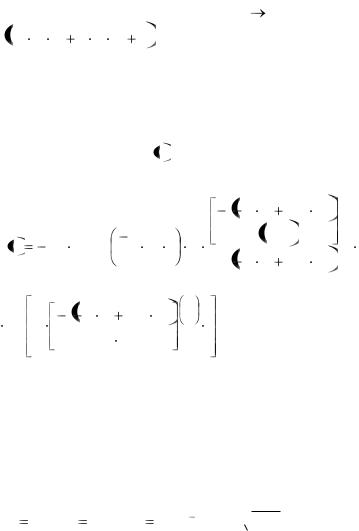
Теперь, чтобы получить решение дифференциального уравнения, к полученному решению-изображению нужно применить операцию обратного преобразования Лапласа. Сделать это можно при помощи оператора invlaplace панели Symbolic (Символьные), т.е.
E |
|
C |
invlaplase, S |
. |
|
|
simplify |
||
S 2 L C r S C |
1 |
При расчете обратного преобразования Лапласа желательно одновременно провести и упрощение получаемого громоздкого выражения, что можно сделать, задействовав одновременно с оператором invlaplace и специальный оператор Simplify (Упростить).
Найденная функция i t после применения обратного преобразования Лапласа будет иметь следующий вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
4 |
L |
C 2 |
|
||||||
i t |
|
2E C exp |
1 |
R |
t |
L |
|
|
L2C |
|
|
|
|
|
|||||
|
2 |
|
L |
|
|
|
R 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
4 |
L |
C |
|
|||||||||
|
|
|
|
R 2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 L |
C |
|
|
|
|
|
|
|
|
|
|
|||||
sin |
|
|
|
2 t . |
|
|
|
|
|
|
|||||||||
2 |
|
L2 |
C |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Такое решение дифференциального уравнения является пусть
изаписанным не в самой удобной форме, но полностью соответствует поставленной задаче и дает такие же результаты как
ипри применении процедуры Given odesolve, как это было сделано в пп.1.5.1 для решения дифференциального уравнения второго порядка.
После соответствующего ввода численных значений будем иметь:
E : 100 L : 0.05 C : 5  10 9 R :
10 9 R :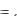
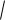 L
L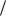 C
C  0,5
0,5
62
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 L |
R2C |
|
i t : |
|
2 E exp |
1 |
|
R |
t |
|
|
L |
|
|
L2 |
C |
|
||
|
2 |
|
|
L |
|
|
|
|
4 L |
R2 C |
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
||
sin |
1 |
|
4 L |
|
C |
2 |
|
t |
|
|
||||||
2 |
|
L2 |
C |
|
|
|
|
|
|
|
||||||
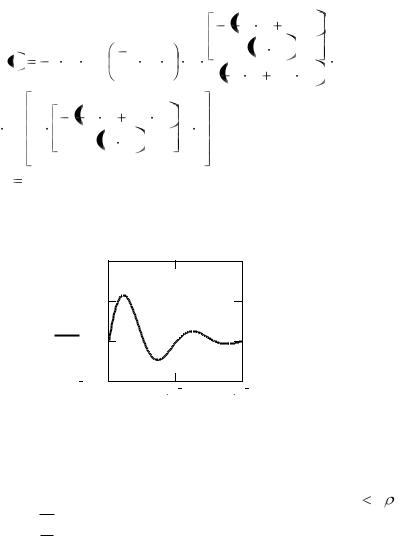
t : 0, 0.000001.. 0.0002
0 .04
0 .02
i( t)
0
0 .02
0
1 1 0 4 |
2 1 0 4 |
t |
|
Рис.2.5. График переходного процесса
Этот результат (рис.2.5) соответствует условию R 2 , где
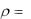
 CL .
CL .
63
2.3. Применение процедур численного дифференцирования и интегрирования к вычислениям методом интеграла Дюамеля
Вычисление интеграла Дюамеля (1.53) предусматривает применение процедур численного дифференцирования и интегрирования. При необходимости можно предварительно осуществить процедуру символьного дифференцирования, которое может быть использовано для подавляющего числа функций, в отличие от того же символьного интегрирования, имеющего весьма ограниченное применение.
Приступая к вычислению производной какой-либо функции, следует найти соответствующий оператор. Оператор производной расположен на панели Calculus (Вычисления) и, поми-
мо того вводится сочетанием клавиш [Shift] + [/], т.е. |
d |
. |
|
||
|
d |
|
Если в результате дифференцирования должна быть получена функция производной, следует обратиться к возможностям символьного вычисления. В качестве оператора вывода следует использовать оператор символьного вывода («→» – Evaluate Symbolically).
При символьном дифференцировании можно оперировать функциями нескольких переменных и функциями с параметрами. Оператор дифференцирования может сочетаться с любым вычислительным оператором.
Пример 2.7. Символьное дифференцирование
d |
|
ln e x sin x |
1 cos x |
|
ln exp x sin x |
, |
|
dx |
|
x |
|
x |
|
x 2 |
|
|
|
|
|
||||
|
d a |
1 |
a 4 . |
||||
|
|
|
|
|
|
|
|
x 1 |
dx x3 |
30 |
|
||||
|
|
||||||
|
|
|
|
|
|
|
|
64

Пример 2.8. Подсчет численного значения при символьном дифференцировании
x :
d |
|
ln ex sin x |
|
1 cos |
|
ln exp |
|
sin |
0,318. |
dx |
|
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Аналогично дифференцированию, интегрирование может быть как численным, так и символьным. Роль численного алгоритма выше в случае интегрирования, чем при вычислении производной. Это связано с тем, что многие функции не имеют первообразной (производную можно вычислить практически для любой функции).
Для ввода определенного интеграла следует использовать оператор панели Calculus (Вычисления) или через клавиши
[Shift] + [7]:
d 
Оператор содержит четыре маркера, которые заполняются в соответствии с принятой в математике формой. Предварительно необходимо присвоить всем параметрам и переменным конкретные значения. Пределы интегрирования должны быть числами. В качестве оператора вывода следует использовать оператор численного вывода (=).
В систему Mathcad встроено несколько численных методов интегрирования. Необходимость этого связана с тем, что алгоритмы численного интегрирования не столь универсальны, как алгоритм дифференцирования. Каждый из них подходит для определенной группы функций. Так, например, такие классические методы, как метод трапеций, средних прямоугольников или Симпсона подходят лишь для гладких непрерывных функций и для небольшого интервала интегрирования. Чтобы подсчитать интеграл с бесконечным пределом или интеграл от функции, имеющей точку разрыва второго рода на границе промежутка, нужно использовать другие методы.
65

Чтобы произвести смену численного метода необходимо осуществить правый щелчок по оператору интегрирования. Откроется его контекстное меню, содержащее список из пяти вариантов возможных алгоритмов интегрирования.
Лучше всего, если по умолчанию отмечен первый вариант Autoselect (Автоматический выбор). Метод интегрирования выбирается при этом автоматически. Однако, в некоторых ситуациях (прежде всего при наличии точек разрыва) система может не справиться с расчетами. В этом случае следует попробовать сменить алгоритм подсчета, сделав выбор из следующих четырех методов:
1.Romberg. Метод, применяемый для вычисления интегралов от функций, не имеющих особенностей.
2.Adaptive. Метод, предназначенный для вычисления интегралов от функций, быстро изменяющихся на промежутке.
3.Infinite Limit (Бесконечный предел). Предназначен для расчета интегралов с бесконечными пределами интегрирования. Самостоятельно выбирать данный метод не придется, поскольку система автоматически переключается на него при введении в оператор интегрирования символа бесконечности.
4.Singular Endpoint (Неопределенность в точке предела интегрирования). Данный метод предназначен для вычисления интегралов от функций, не существующих в одной или в обеих точках пределов интегрирования (так называемые несобственные интегралы второго рода).
Точность результатов интегрирования можно регулировать заданием оператора TOL перед интегралом.
По умолчанию TOL:= 10-3. Можно задавать любую величину
до 10-13.
Так, например, точное аналитическое решение интеграла
e x sin x dx |
1 |
0.5, |
|
|
|||
2 |
|||
|
|
0
а при обычной точности (TOL = 10-3)
66

e x  sin x dx 0,499999999986754,
sin x dx 0,499999999986754,
0
но при TOL:=10-13 имеем, что
e x  sin x dx 0.5.
sin x dx 0.5.
0
Приведем теперь пример использования численных методов при определении отклика цепи на входное воздействие с помощью интеграла Дюамеля.
Воспользуемся условиями задачи из примера 1.4, когда на
вход |
RL |
цепи (рис.1.27(а)) с |
переходной характеристикой |
|||
|
|
R |
t |
|
|
|
|
|
|
|
|
|
|
h t |
e L |
воздействует напряжение |
||||
|
|
|
|
|
0 при t |
0 |
|
|
|
|
u t |
U eat |
при 0 t t |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
0 при t |
t1. |
Пример 2.9. Зададимся конкретными значениями величин,
т.е. t : 0,0001..0.01 |
R : 100 Ом L 100 10 3 Гн a 100 |
t1: 0.005 U 10 В |
|
Для интервала 0 t |
t1 получим, что |
u1 t  : U
: U  e
e
R t t
t t
L
0
d |
|
|
R t |
|
|
a |
|
L |
|
||
|
U e |
|
e |
d , |
|
d |
|
|
|||
а для интервала t t1 будем иметь отклик
|
R t |
t1 |
|
|
|
|
|
|
u2 t U e L |
|
|
|
|
0 |
d |
|
|
R t |
|
|
|
R t |
t1 |
||
a |
|
|
|
at1 |
|
|
|
|
||
|
L |
|
|
L |
|
|
||||
|
U e |
|
e |
U e |
|
e |
. |
|||
d |
|
|
|
|
||||||
Вычисляем результирующий отклик с учетом двух интервалов и строим график (рис.2.6), т.е.
u3 t : if t t1, u1 t , u2 t
67
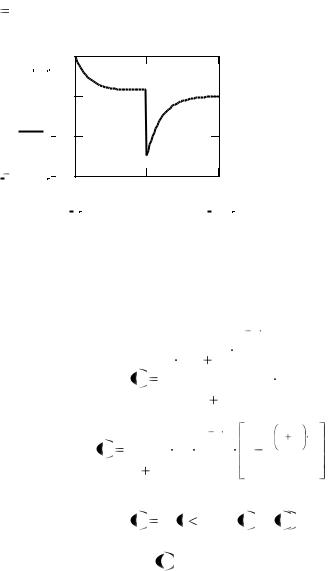
t : 0, 0.0001..0.008
10 |
10 |
|
|
|
0 |
u3(t) |
|
|
10 |
14.927 |
20 0 |
|
|
|
0 |
0.005 |
0.01 |
t |
0.01 |
Рис.2.6. График переходного процесса
Вычисление отклика по формулам, полученным в примере 1.4, осуществляется в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
eat |
|
|
R e L |
|
|
|
|
|||||||||
u4 t : |
|
|
|
|
|
|
L |
U |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
a |
|
|
R |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
U |
|
|
|
|
R |
|
|
R t |
|
|
|
|
a |
R |
t1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|||||
u5 t : |
|
|
|
|
e |
L |
1 e |
|
|
|||||||||||
a |
R |
|
L |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
u3 t : if t t1, u4 t ,u5 t |
|
|
||||||||||||||||||
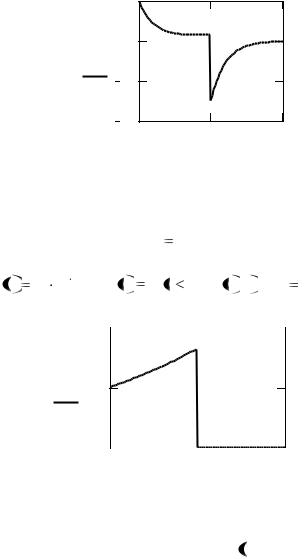
и график отклика u3 t |
(рис.2.7) |
совпадает с откликом |
||||||||||||||||||
(рис.2.6), рассчитанным численным методом.
68
10 |
|
|
|
0 |
|
|
|
u3(t) |
|
|
|
10 |
|
|
|
20 |
0 |
0.005 |
0.01 |
|
|
t |
|
Рис.2.7. График при расчете по формулам
Представление входного воздействия, используя Mathcad при
конкретных значениях |
a |
100, можно осуществить в виде |
||||
графика (рис.2.8), следующим образом |
|
|
||||
u7 t : U ea t u8 t : |
if t |
t1,u7 t , 0 |
t : 0, 0.0001.. 0.008 |
|||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
u8(t) 10
0 |
|
|
|
|
|
0 |
0.005 |
0.01 |
|||
|
|
|
t |
|
|
Рис.2.8. График входного воздействия
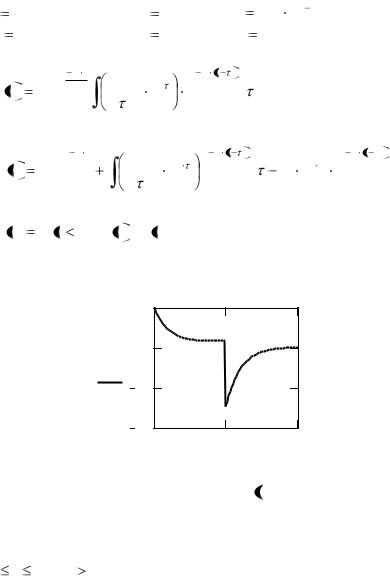
Листинг 2.1 расчетов с графиком h t  (рис.2.9) для примера
(рис.2.9) для примера
1.4 будет иметь следующий вид. Листинг 2.1, Mathcad
69
t : |
0, 0.0001.. 0.01 |
R : |
100 |
L : |
100 10 3 |
a : |
100 |
t1: |
0.005 |
U : |
10 |
u1 t : U  e
e
u2 t : U  e
e
R t |
t |
|
d |
|
|
|
|
|
R t |
|
|
|
|
|
||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||
L |
|
|
U |
e |
|
e |
|
L |
d |
|
|
|
||||
|
0 |
|
d |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R t |
|
t1 |
d |
|
|
|
|
|
R t |
|
|
|
|
R t t1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
a t1 |
|
|
|
L |
|
|
|
|
U e |
|
e |
L |
|
d U e |
e |
L |
||||
|
|
0 |
|
d |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u3 t : if t t1, u1 t , u2 t
: if t t1, u1 t , u2 t
10 |
|
|
|
0 |
|
|
|
u3(t) |
|
|
|
10 |
|
|
|
20 |
0 |
0.005 |
0.01 |
|
|
t |
|
Рис.2.9. График результата расчета с h t 
В случае применения для расчетов интеграла Дюамеля на основе импульсной характеристики (1.56), переходной процесс по примеру 1.4. также вычисляется по частям на интервалах 0 t t1 и t t1 . Расчеты с применением системы Mathcad и график (рис.2.10) для этого случая показаны в листинге 2.2.
70
