
Методическое пособие 657
.pdf
Пример 1.4. Найти напряжение на выходе цепи (рис.1.27(а)), если напряжение на ее входных зажимах изменяется во времени по закону
|
0 |
при t |
0 |
|
|
|
u t |
U e t |
при 0 |
t t |
|
|
|
1 |
|
|
1 |
|
|
|
|
0 |
при t |
t1 , |
|
|
|
|
|
|
|
|
R |
t |
|
|
|
|
|
|
|
а переходная характеристика цепи h t |
e L . |
|||||
График входного воздействия u1 t |
на электрическую цепь |
|||||
показан на рис.1.27 (б).
Рис.1.27. RL -цепь (а) и входное воздействие (б)
Решение. В интервале времени 0 t t1 воспользуемся формулой интеграла Дюамеля (1.53)
|
|
t |
|
f t |
f1 0 h t |
f1 h t |
d . |
0
Подставляя соответствующие значения, получаем, что
t |
du1 |
|
|
|
u2 t u1 0 h t |
|
h t |
d |
|
d |
||||
0 |
|
|
||
|
|
|
51
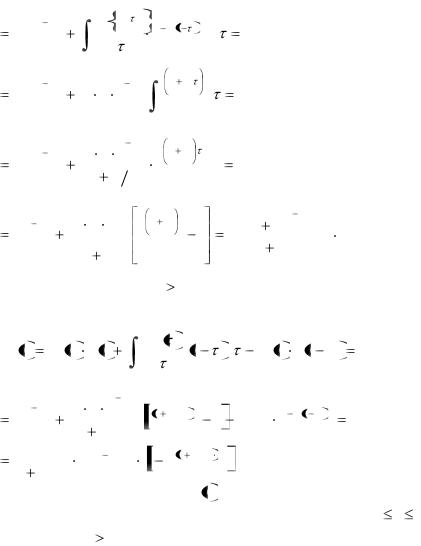
U  e
e
U  e
e
U  e
e
R |
t |
|
t |
d Ue |
a |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
L |
|
|
|
|
|
|
e |
R t |
|
|
|
/ L |
d |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
d |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R |
t |
|
|
|
|
|
Rt |
|
t |
a |
|
R |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|||
L |
U |
|
a e |
|
L |
|
e |
|
|
d |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
Rt |
|
|
a |
R |
|
|
t |
|||
t |
U |
|
a e |
L |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
L |
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
L |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
||||
|
|
|
|
a |
R L |
|
|
|
|
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
Rt |
|
|
|
R |
|
|
|
|
|
|
Rt |
|
|
|||||
|
|
|
t |
U a e L |
a |
|
t |
|
|
aeat |
Re L / L |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
L |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
Ue |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
1 |
|
|
|
|
|
|
U. |
|||
|
|
|
|
a |
|
R |
|
|
|
|
|
|
a |
R / L |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В интервале времени |
t |
t1 |
получаем с учетом скачка в мо- |
|||||||||||||||||||||||||||
мент t1 , что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
du1 |
|
|
|
|
|
|
|
|
|
|
||||
u2 t |
|
|
u1 0 h t |
|
h t |
|
d u1 t h t t1 |
|
||||||||||||||||||||||
|
|
d |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Rt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
U |
|
a e L |
e a R / L t1 |
|
1 Ueat1 |
e R t t1 L |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Ue |
|
L |
|
|
|
|||||||||||||||||||||||||
|
|
a R / L |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
U |
|
|
|
R |
e Rt / L |
1 e a R / L t1 . |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
a |
|
R / L |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Результирующий отклик |
|
u2 |
t определяется последователь- |
|||||||||||||||||||||||||||
ной стыковкой выходного воздействия на интервале 0 t t1
и интервале t t1.
Возможно также определение реакции цепи на произвольное внешнее воздействие по ее импульсной характеристике. Выражение для этого случая можно получить из формулы (1.52), используя правило интегрирования по частям и учиты-
52
вая соотношение между переходной и импульсной характеристиками цепи (1.43), т.е.
|
|
t |
|
|
|
uвых t |
u t h 0 |
u |
g t |
d , |
(1.56) |
|
|
0 |
|
|
|
где h 0 |
- значение h t |
цепи при t |
0. |
|
|
Выражение (1.56) можно использовать для определения реакции цепи и в том случае, когда внешнее воздействие на цепь описывается кусочно-непрерывной функцией. При этом интервал интегрирования разбивается на несколько промежутков в соответствии с интервалами непрерывности входного входного сигнала u t .
Так, если на цепь воздействует колебание сложной формы
f t |
(рис.1.26), то в случае применения импульсной характе- |
||||||||
ристики, отклик цепи uвых |
t необходимо определять с учетом |
||||||||
различных интервалов времени: |
|
|
|
|
|||||
а) в первом интервале времени |
0 t |
t1 |
|
|
|||||
|
|
|
|
|
|
t |
|
|
|
|
|
uвых t |
f1 t |
h 0 |
f1 |
g t |
d |
; |
|
|
|
|
|
|
|
0 |
|
|
|
б) во втором интервале времени |
t1 |
t t2 |
|
|
|||||
|
|
t1 |
|
|
|
|
t |
|
|
uвых t |
f1 |
g t |
d |
f2 t |
h 0 |
f2 |
g t |
d ; |
|
|
|
0 |
|
|
|
|
t1 |
|
|
в) в третьем интервале времени |
t2 |
t |
|
|
|||||
|
|
t1 |
|
|
t2 |
|
|
|
|
uвых |
t |
f1 |
g t |
d |
f 2 |
g t |
d |
f3 t |
h 0 |
|
|
0 |
|
|
t1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
f3 |
g t |
d . |
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
53
2.ПРИМЕНЕНИЕ ЭВМ ДЛЯ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ
Для расчета переходных процессов в линейных электрических цепях достаточно успешно может быть использован программный продукт компьютерной математики Mathcad по-
следних версий: Mathcad 8/2000, Mathcad 2001 [ 3, 4].
Применение пакета Mathcad позволяет, используя стандартные программы, получить численное решение дифференциального уравнения цепи с определением переходного процесса и построения его графика.
Здесь имеются в виду так называемые обыкновенные дифференциальные уравнения (ОДУ). Это уравнения, в которые входят производные только по одной переменной.
Mathcad, к сожалению, не позволяет непосредственно находить аналитические решения таких дифференциальных уравнений, однако реально упрощает выполнение различных вычислительных этапов при поиске указанных решений традиционными методами .
Переходные процессы, отражаемые ОДУ, обычно описывают изменение анализируемой характеристики с течением времени, а начальные условия должны определяться в момент времени t 0 .
Заданные таким образом дифференциальные уравнения называются задачами Коши [2].
Методы численного решения ОДУ в форме задачи Коши разработаны весьма досконально. Самыми популярными из них заслуженно являются алгоритмы Рунге-Кутта [3], успешно используемые для решения подавляющего большинства дифференциальных уравнений.
Решение одного линейного дифференциального уравнения в Mathcad может быть реализовано в двух формах: в виде вычислительного блока или в виде встроенных функций. Первая форма предпочтительнее с точки зрения наглядности представления решения и технической простоты.
54

2.1. Решение дифференциальных уравнений с помощью вычислительного блока Given-Odesolve
Описание функции Odesolve можно найти в [5].
Чтобы реализовать блок Given-Odesolve, необходимо иметь составленное заранее по электрической цепи в соответствии с правилами (пп.1.2-1.3) дифференциальное уравнение (1.8) или (1.11) и далее выполнить следующую последовательность действий:
1.Ввести вводное слово Given (дано).
2.Ниже вводного слова ввести дифференциальное уравнение типа (1.8) или (1.11). Это дифференциальное уравнение должно быть строго линейным (то есть высшая производная в нем не должна иметь никаких сомножителей или степенных показателей). Подобное ограничение связано с особенностями используемого (по умолчанию) системой при решении дифференциального уравнения в форме вычислительного блока Given-Odesolve метода Рунге-Кутта 4-го порядка точности.
3.Производные в выражении дифференциального уравнения необходимо задать при помощи специальных операторов панели Calculus (вычисления) отдельно для производной первого порядка и производных произвольного порядка.
4.Искомые функции могут быть определены произвольным образом с соблюдением общих правил синтаксиса Mathcad.
5.В качестве знака равенства в дифференциальном уравнении следует использовать логическое равенство (=) из иконки «Boolean».
6.Кроме дифференциального уравнения, внутри блока необходимо задать и соответствующие начальные условия. Число начальных условий определяется порядком дифференциального уравнения. Так для уравнения первого по-
рядка |
необходимо задать |
одно начальное условие при |
|
t 0, |
а для уравнения второго порядка еще |
и значение |
|
первой производной при t |
0. Оно вводится |
через соот- |
|
55

ветствующий штрих, который ставится сверху переменной при помощи сочетания [Ctrl] + [F7] и при этом не требуется устанавливать значок ввода степени.
7.Затем следует задействовать специальную функцию odesolove (t, в, [step] ), где t – переменная, от которой зависит искомая функция; в – правая единица интервала поиска решения, левая граница которого определяется при задании начальных условий. Обязательное условие – значение
«в» должно лежать правее.
Step – определяет число шагов, используемых численным методом Рунге-Кутта.
Задание step не является обязательным, и по умолчанию этот параметр определяется таким образом, чтобы длина шага равнялась 0,1. Нельзя задавать step равным 1, так как при этом возникает неопределенность. При уменьшении значения step увеличивается время расчетов.
Затем, перед построением графика переходного процесса, необходимо ввести изменение величины t для более полного отражения сущности возникающих отклонений тока или напряжения. Изменения вводятся по образцу:
t : 0, доля шага в .. в.
Приведем примеры решения дифференциальных уравнений первого и второго порядков с использованием блока GivenOdesolve.
Пример 2.1. Найти решение дифференциального уравнения, составленного в примере 1.1.
Выражение для дифференциального уравнения берем из (1.8), т.е.
RC |
duc |
uc |
E2 , |
|
dt |
||||
|
|
|
||
а начальное условие uc 0 |
|
uc 0 |
E1. |
Теперь зададимся для определенности значениями элементов:
R 104 Ом, C 10 10 |
6 Ф, E 10 В, |
E |
2 |
20 В. |
|
1 |
|
|
56

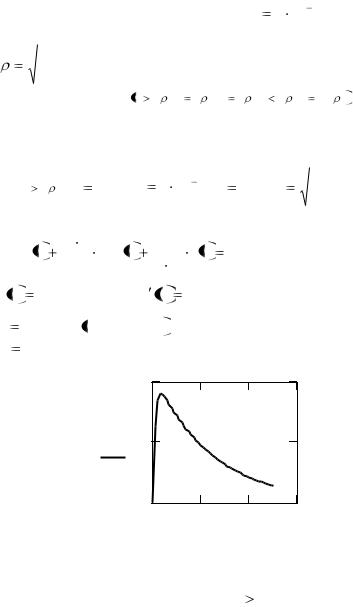
Последовательность ввода и результат в виде графика (рис.2.1) при определении переходного процесса будет иметь следующий вид.
R : |
104 C : |
10 10 |
6 E : 10 |
E |
2 |
: |
20 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R C |
d |
u t |
u t |
E |
|
u 0 |
|
E |
|
u : odesolve t,0.4,10 |
||||||
|
|
2 |
|
|||||||||||||
|
|
dt |
|
|
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
t : |
0, 0.001.. 0.4 |
|
|
|
|
|
|
|
|
|
||||||
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
u( t) |
1 5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
0 .2 |
|
0 .4 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
Рис.2.1. График переходного процесса
Пример 2.2. Найти решение дифференциального уравнения, составленного в пп.1.3. [(1.10), (1.11)].
Выражение для дифференциального уравнения берем из
(1.11), т.е.
L |
d 2i |
R |
di |
1 |
i 0. |
|
|
|
|
|
dt 2 |
dt |
|
C |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Начальные условия i 0 |
i 0 |
|
0 и из (1.14) |
di |
|
E |
при |
|||
|
dt |
|
L |
|||||||
|
|
|
|
|
|
|
|
|
||
t 0.
57
Теперь зададимся для определенности конкретными значе-
ниями элементов цепи: L = 0,05 Гн, C |
5 10 9 |
Ф, а необходи- |
||||
мую величину R будем брать |
при вычисленном значении |
|||||
|
|
|
|
|||
|
L |
, изменяя ее для получения различных видов пере- |
||||
|
|
|||||
|
C |
|
|
|
||
ходных процессов R 2 (R 5 ), R |
2 , R |
2 (R |
0,5 ) . |
|||
Последовательность ввода и результаты расчетов в виде графиков (рис.2.2-2.4) при определении переходных процессов будут следующими:
а) |
(R |
2 |
) L |
0.05 C |
5 10 9 |
E 100 |
R |
|
L |
|
||||||||
|
|
|||||||||||||||||
C |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
2 |
i t |
|
R 5 |
|
d |
i t |
1 |
|
i t |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dt 2 |
|
L |
|
dt |
L C |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i 0 |
|
0 |
|
|
|
|
i |
0 |
|
E |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
L |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i : |
|
odesolve t, 0.01, 2000 |
|
|
|
|
|
|
|
|
||||||||
t : 0, 0.000001.. 0.0002
|
0 .2 |
|
|
|
i( t) |
0 .1 |
|
|
|
|
0 0 |
0 .02 |
0 .04 |
0 .06 |
|
|
|
t |
|
Рис.2.2. Переходной процесс при R 2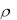
58
б) ( R |
2 |
) L : |
0.05 C : |
5 10 |
|
9 E : |
100 |
R : |
L |
|
||||||||
|
C |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d |
2 |
i t |
R 2 d |
i t |
|
1 |
i t |
0 |
i 0 0 |
i 0 |
E |
|||||||
dt 2 |
|
|
|
|
|
|||||||||||||
|
|
L |
dt |
|
L |
C |
|
|
|
|
|
|
|
L |
||||
|
|
i : |
odesolve t, 0.01, 2000 |
|
|
|
|
|
|
|
|
|||||||
t : |
|
0, 0.000001.. 0.0002 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 .4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i( t) |
|
0 .2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
0 .02 |
|
0 .04 |
|
0 .06 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
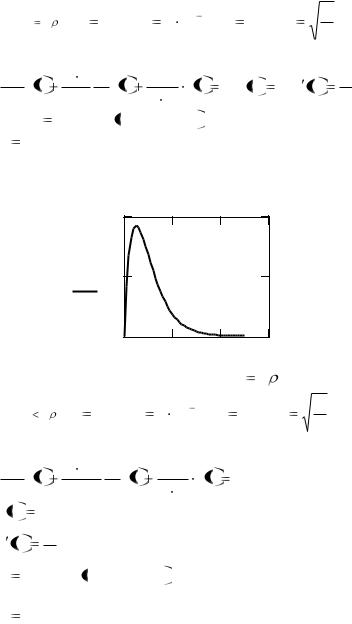
Рис.2.3. Переходной процесс при R |
2 |
|
|
|
|
|||||||||||||
в) |
(R |
2 |
) L : |
0.05 C : |
5 10 9 |
E : 100 |
R : |
|
L |
|
||||||||
|
C |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d |
2 |
i t |
R 0,5 d |
i |
t |
|
1 |
i |
t |
0 |
|
|
|
|
|
|||
dt 2 |
L |
|
dt |
L |
C |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i 0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
0 |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i : |
|
odesolve t, 0.01, 2000 |
|
|
|
|
|
|
|
|
|
|||||||
t : |
|
0, 0.000001.. 0.0002 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|
0 .04 |
|
0 .02 |
|
i( t) |
|
0 |
|
0 .02 |
1 1 0 4 |
0 |
|
|
t |
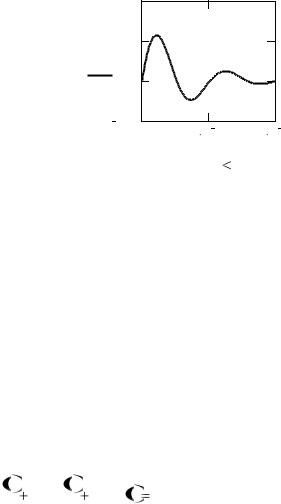
Рис.2.4. Переходной процесс при R
2 1 0 4
2
2.2. Решение дифференциальных уравнений операторным методом
Если дифференциальное уравнение, которое необходимо решить, имеет постоянные коэффициенты, то для этих целей можно использовать преобразование Лапласа. Используя его свойства, переводят дифференциальное уравнение в соответствующее алгебраическое, аналитически решив которое и применив к нему операцию обратного преобразования Лапласа, можно получить решение дифференциального уравнения в общем виде.
Возьмем в качестве примера для решения дифференциальное уравнение (1.11), описывающее процессы в последовательном колебательном контуре
d 2i t |
|
R di t |
1 |
i t 0. |
|||
|
|
|
|
|
|
|
|
dt 2 |
|
L dt |
|
LC |
|||
|
|
|
|||||
Приступая к решению уравнения, получим прежде всего его изображение с помощью прямого преобразования Лапласа. Для этого используем специальный оператор «laplace» (Лапласа) панели Symbolic (символьные): ● laplace, ● →.
60
