
Методическое пособие 657
.pdf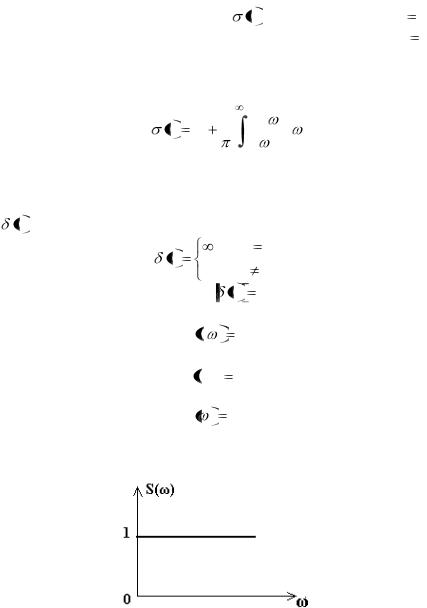
о наличии в исходной функции t (1.36) скачка при t |
0. |
Для образования этого скачка в соответствии с (5.37) при t |
0 |
необходимо осуществить суммирование бесконечно большого числа синусоидальных составляющих, что может быть выражено формулой [10]
t |
1 |
|
1 |
|
sin t |
d , |
2 |
0 |
|
||||
|
|
|
||||
|
|
|
|
|||
которая отражает спектр единичного импульса в интегральной форме.
Единичный импульс (1.38), обозначаемый в формулах как
t - это сигнал, для которого |
|
||
t |
при t |
0, |
|
0 при t |
0. |
||
|
|||
В соответствии с (1.42) L t |
1.Следовательно, и спек- |
||
тральная плотность единичного импульса равна единице:
S j |
1 |
(5.40) |
или
S j 1
1  e j0 ,
e j0 ,
откуда модуль спектральной плотности
S |
1. |
(5.41) |
Согласно формуле (5.41) у единичного импульса сплошной равномерный спектр (рис.5.12).
Рис.5.12. Спектральная плотность единичного импульса
141

Получить спектр единичного импульса в интегральной форме можно, применяя формулу обратного преобразования Фурье (5.22) к спектральной функции единичного импульса
(5.41), т.е.
t |
1 |
|
S |
j e j t d |
1 |
|
e j t d |
||
|
|
|
|
|
|||||
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|||
1 |
|
|
cost |
j sin t d |
1 |
cos td |
|||
|
|
|
|
|
|
||||
2 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|||
1 cos td .
0
Единичный импульс  t физически не может быть реали-
t физически не может быть реали-
зован. Он, как математическая функция, используется в теории сигналов и в анализе передачи сигналов по электрическим цепям. Единичный импульс может быть получен следующим образом. Так, если имеется прямоугольный видеоимпульс длительностью tu и высотой 1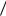 tu , то площадь такого импульса
tu , то площадь такого импульса
равна единице. Если одновременно уменьшать длительность импульса и увеличивать его высоту в одинаковое количество раз, то площадь импульса остается неизменной; при tu 0 получаем единичный импульс 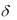 t .
t .
5.7.Спектральный метод анализа электрических цепей
Понятие о спектрах сигналов может быть применено к задаче анализа электрических цепей. При этом должны быть известны: временная функция входного сигнала и комплексный ко-
эффициент передачи цепи K j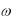 . Для решения этой задачи
. Для решения этой задачи
входной сигнал необходимо представить в виде элементарных (гармонических) сигналов. Затем определить реакцию цепи на каждый такой элементарный сигнал. Заключительным этапом
142
решения задачи является суммирование всех элементарных сигналов на выходе цепи.
Если входной сигнал является непериодическим, то амплитуда элементарного гармонического колебания в спектре сигнала определяется через спектральную плотность формулой (5.24)
dA 1 S1 j d ,
где S1 j
j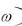 - спектральная плотность входного сигнала, определяемая с помощью прямого преобразования Фурье (5.21)
- спектральная плотность входного сигнала, определяемая с помощью прямого преобразования Фурье (5.21)
S |
j |
u t e j t dt. |
1 |
|
1 |
Так как комплексный коэффициент передачи электрической цепи
K ( j ) U2 , U1
то элементарная амплитуда в спектре выходного сигнала |
dU |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
определяется выражением |
|
|
|
|
|
|
|
|
||
dU2 |
K j |
dU1 |
|
K j |
1 |
S1 j d . (5.42) |
||||
|
|
|
|
|
|
|
|
|
|
|
С учетом того, что |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
dU2 |
|
S2 |
j |
d |
, |
|
|
|
|
|
|
|
|
|
|
|||||
то после ее подстановки и преобразований в (5.42) получаем зависимость
|
|
S 2 j |
S1 j |
K j , |
(5.43) |
|
|
|
|
|
|
где S2 j |
- спектральная плотность выходного сигнала. |
||||
Следовательно, |
спектральная |
плотность выходного |
сигнала |
||
S2 j |
равна произведению спектральной плотности входно- |
||||
го сигнала S1 j |
на комплексный коэффициент передачи це- |
||||
пи K j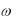 . Заменяя комплексные величины, входящие в урав-
. Заменяя комплексные величины, входящие в урав-
143

нение (5.43), выражениями через их модули и аргументы, получаем
S2 |
e |
j |
S2 |
S1 |
e |
j |
S1 |
|
|
K |
e |
j |
; |
|
|
|
|
|
|
|
|||||||
S2 |
e |
j |
S2 |
S1 |
K |
|
e |
j |
S1 |
|
. |
(5.44) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||
Приравнивая модули и аргументы в выражении (5.44), получаем формулы:
|
S2 |
|
S1 |
|
K , |
|
s2 |
|
|
s1 |
. |
|
|
|
|
||
Определив S2 j |
и применив обратное преобразование Фу- |
||||
рье, можно найти напряжение на выходе цепи |
|||||
|
u2 t |
1 |
S |
|
j e j t d . |
|
|
2 |
|||
|
2 |
||||
|
|
|
|
|
|
Если на входе цепи действует периодический сигнал, то производится также разложение его на гармоники, которые определяются комплексной амплитудой n -й гармоники
|
|
|
|
|
|
T 2 |
|
|
|
|
|
|
|
2 |
|
|
jn t |
|
|
|
|
|
An1 |
|
|
u1 t |
e |
|
dt. |
|
|
|
|
T |
|
||||
|
|
|
|
|
T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем определяется спектр выходного сигнала как |
|||||||||
|
|
|
|
An2 |
An1 |
K n |
, |
|
|
|
|
|
|
|
|
|
|
|
|
где |
An2 |
- комплексная амплитуда n |
й гармоники выходного |
||||||
|
|
|
|
|
|
|
|
|
|
сигнала, |
K n |
комплексный коэффициент передачи цепи |
|||||||
|
|
|
|
|
|
|
|
|
|
для |
n |
й гармоники. |
|
|
|
|
|
|
|
Заключительный этап – суммирование гармоник на выходе цепи:
|
|
1 |
|
|
|
jn t |
|
u2 |
t |
|
|
An2 |
e |
|
. |
2 n |
|
||||||
|
|
|
|
|
|
||
Изложенную выше методику можно применять в различных случаях анализа электрических цепей, в том числе и для опре-
144
деления переходных процессов в линейных цепях при разных видах входных воздействий, а также использовать для определения условий безыскаженной передачи сигналов через электрическую цепь.
5.8. Условия безыскаженной передачи сигналов через электрическую цепь
Рассмотрим условия, которым должны удовлетворять частотные характеристики электрической цепи, чтобы сигнал проходил через цепь без искажения своей формы.
Очевидно, что математическим условием неискаженной передачи сигнала является выражение
u2 t ku1 t t0 , |
(5.45) |
где k 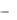 постоянный множитель; t0
постоянный множитель; t0  время запаздывания (за-
время запаздывания (за-
держка).
Выражение (5.45) означает, что передача сигнала будет считаться неискаженной, если в результате прохождения его через цепь, он изменится на постоянный множитель k и сдвинется (задержится) по времени на величину t0 .
Учтем эти условия через формулы для спектральных плотностей и тогда получим, что
S |
|
j |
u t |
|
e |
j |
t dt, |
|
|
|
|
|
|
||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
S |
2 |
j |
u |
2 |
t e |
|
i t dt |
ku t t |
0 |
|
e j t dt |
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
k |
u t |
t |
|
|
e |
j |
t |
|
j |
e |
j |
|
t0 |
, |
|
0 |
|
|
|
dt kS |
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
где последнее выражение определено с учетом теоремы запаздывания (5.4), которая говорит о том, что задержка колебания
145
на время t0 эквивалентна умножению его спектра на множи-
тель e j t0 .
Таким образом, комплексный коэффициент передачи такой электрической цепи описывается формулой
|
|
|
j |
|
|
|
|
|
|
|
|
S2 |
|
|
j t0 |
|
j |
|
|
K |
j |
S1 |
j |
k |
e |
|
K e |
|
. |
|
|
|
|
|
|
|
|
|
|
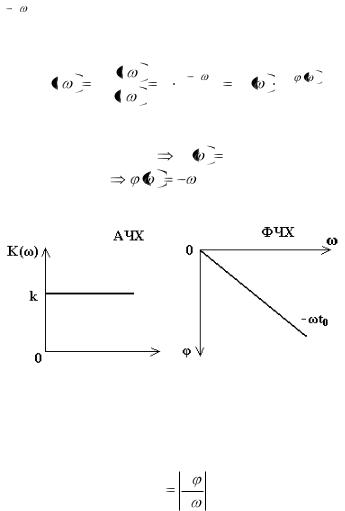
Следовательно, для неискаженной передачи сигналов частотные характеристики электрической цепи должны быть такими:
АЧХ K |
k, |
(5.46) |
ФЧХ |
t0 . |
(5.47) |
Графики зависимостей (5.46) и (5.47) показаны на рис.5.13.
Рис.5.13. Графики АЧХ и ФЧХ электрической цепи для неискаженной передачи сигнала
Задержка сигнала на время t0 , создаваемая цепью без искажений определяется наклоном ФЧХ (рис.5.13), т.е.
d
t0 d .
Частотные характеристики реальных электрических цепей могут лишь приближаться к этим идеальным характеристикам (рис.5.13) в ограниченном диапазоне частот.
146
6. ПРИМЕНЕНИЕ ЭВМ ДЛЯ РАСЧЕТА СПЕКТРАЛЬНОГО ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
Для расчета спектра сигнала достаточно успешно может быть использован программный продукт компьютерной математи-
ки Mathcad [4].
Процедура определения спектрального представления функций предусматривает, как правило, применение методов их численного интегрирования. Основные правила и приемы при использовании этих методов рассматривались в расчете переходных процессов (п.2.3).
Последовательность вычисления спектра сигнала на основе ЭВМ включает в себя следующие этапы:
1.Представление функции сигнала в виде аналитической записи, соответствующей правилам пакета Mathcad;
2.Запись выражений для коэффициентов гармоник и их вычисление;
3.Построение графиков спектра амплитуд и спектра фаз гармоник.
6.1. Аналитическая запись сигналов при определении их спектров
Аналитическая запись рассматриваемого сигнала, как правило, осуществляется в пределах одного периода, так как этого обычно достаточно для определения коэффициентов спектра Фурье.
В программе Mathcad для представления сигналов наиболее удобно использовать функцию условных выражений [4]: if (условие, выражение 1, выражение 2).
Если в этой функции условие выполняется, то будет вычисляться выражение 1, в противном случае – выражение 2. Возможен также расширенный вариант применения функции условных выражений: if (условие 1, выражение 1), if (усло-
вие 2, выражение 2, выражение 3). Если здесь выполняется
147

условие 1, то будет вычисляться выражение 1, в противном случае вступает в силу условие 2, при выполнении которого вычисляется выражение 2, в противном случае – выражение 3. В том случае, когда число условий больше трех, то следует использовать панель Programming (Программирование), раздела Math (Математические) и воспользоваться языком программирования Mathcad (рис.6.1)
Рис.6.1. Рабочая панель Programming (Программирование)
Для того чтобы написать программу, прежде всего, должен быть создан специальный обособленный от остального документа блок. Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения алгоритма. Для построения единичного элемента программного блока следует нажать кнопку команды Add Line (Добавить линию) панели Programming (рис.6.1). В области курсора появится следующий объект
в который следует внести наименования функций и условия, а число маркеров, при необходимости можно увеличить, нажав необходимое число раз «горячую» клавишу « ] ».
Приведем примеры записи некоторых функций с различным количеством условий.
148

Для формирования прямоугольного импульса следует осуществить следующую запись
S t : if t |
T |
, 1, 0 . |
(6.1) |
|
2 |
||||
|
|
|
Для получения другой длительности импульса следует в (6.1) изменить T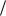 2 на соответствующую величину. Изменение амплитуды импульса и его полярности обеспечивается подстановкой иных значений в позиции, следующей за T
2 на соответствующую величину. Изменение амплитуды импульса и его полярности обеспечивается подстановкой иных значений в позиции, следующей за T 2 .
2 .
Иной вид импульса, например, пилообразный получается, если задать условия
u t : if t T , kt, 0 . |
(6.2) |
График пилообразного импульса в соответствии с (6.2) показан на рис.6.2.
Рис.6.2. График импульса в соответствии с условиями (6.2)
Иная форма пилообразного импульса (рис.6.3) может быть задана условиями:
u t : if t |
T |
, y1 , y 2 , |
(6.3) |
|
2 |
||||
|
|
|
y1 kt, y2 k t T .
149
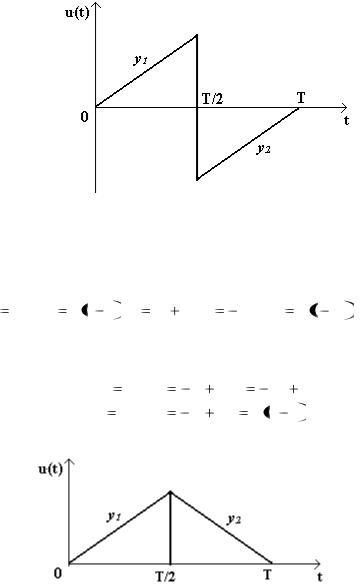
Рис.6.3. График импульса по условиям (6.3)
Условия (6.3) получаются из совместного рассмотрения уравнения прямых линий и определения необходимых коэффициентов, т.е.:
y1 kt, y2 k T t , 0 kt b , b |
kt, y2 k t T . |
Аналогично можно получить выражение для функции, имеющей график, показанный на рис.6.4:
y1 kt, y2 |
kt b, 0 |
kT b, |
(6.4) |
|
b kT, y2 |
kt kT k T t . |
|||
|
||||
Рис.6.4. График пилообразного импульса
150
