Методическое пособие 657
.pdf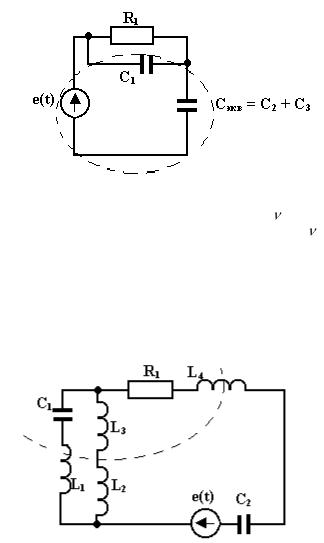
Рис.1.3. Емкостный контур цепи
Таким образом, из предполагаемой сложности цепи = 3 в соответствии с рис.1.3, после преобразований остается сложность цепи = 1, которая получается с учетом объединения элементов С2 и С3 и наличия одного емкостного контура, состоящего из С1, Сэкв, е(t).
Уменьшает порядок сложности цепи и наличие в цепи, так называемых индуктивных сечений. Индуктивное сечение – это индуктивный узел, т.е. узел к которому подключены ветви, в каждой из которых есть только индуктивные элементы или индуктивности с другими элементами R и С или источниками тока i(t). На рис.1.4 представлен такой узел (индуктивное сечение), обозначенное пунктирной линией.
Рис.1.4. Индуктивное сечение
На рис.1.5 показано индуктивное сечение с элементами L1, L2, L3 и источником тока i(t), объединенных в один узел.
11
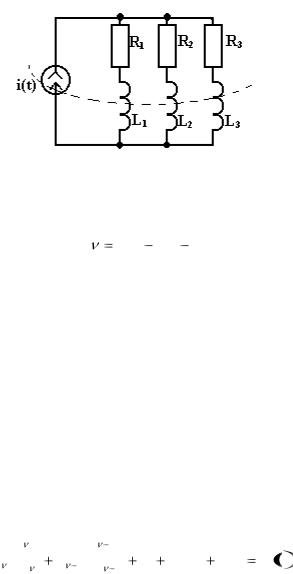
Рис.1.5. Индуктивное сечение из параллельных ветвей
Таким образом, порядок сложности линейной цепи, составленной только из идеализированных пассивных элементов и независимых источников тока или напряжения
PLC neк quc ,
где PLC - общее число реактивных элементов; neк - число независимых емкостных контуров; quc - число независимых индуктивных сечений. Это
возможно в связи с тем, что в емкостном контуре напряжение на любом из конденсаторов такого контура может быть выражено через напряжения других емкостей с помощью уравнения баланса потенциалов, составленного для данного емкостного контура. Для индуктивного сечения (узла) ток, а следовательно, и энергия любой из индуктивностей, входящей в индуктивное сечение, может быть выражена через токи других индуктивностей на основании уравнений баланса токов, составленных для данного сечения.
1.2. Классический метод анализа переходных процессов
Он основан на классическом методе решения обыкновенных дифференциальных уравнений. Как известно, общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами
a |
d y |
a |
|
d 1 y |
a |
dy |
a |
|
y f t |
(1.3) |
|
|
1 |
|
|
|
0 |
||||||
|
dt |
|
dt |
1 |
1 |
dt |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
равно сумме частного решения этого уравнения и общего решения однородного дифференциального уравнения (правая часть равна нулю).
12
Общее решение однородного дифференциального уравнения характеризует так называемые свободные процессы в цепи, т.е. процессы после коммутации в отсутствие внешних источников энергии.
Таким образом, характер свободных процессов не зависит от вида внешнего воздействия на цепь, а определяется только параметрами ee пассивных элементов.
Частное решение уравнения (1.3) определяет принужденный режим работы цепи, т.е. режим, задаваемый действующими в цепи независимыми источниками энергии.
Следовательно, общее решение имеет вид
y t yсв t yпр t .
Свободная составляющая реакции цепи с течением времени
затухает lim yсв 0, поэтому принужденная составляющая ре-
t
акции цепи представляет собой установившееся значение искомого тока или напряжения после коммутации, т.е.
yпр |
lim y . |
|
t |
Для определения принужденной составляющей реакции цепи можно воспользоваться рассмотренными ранее методами анализа линейных цепей в установившемся режиме.
Если после коммутации токи всех независимых источников не изменяются, то с течением времени в цепи после коммутации установится режим постоянного тока.
Если после коммутации цепь находится под гармоническим воздействием, то принужденная составляющая также будет гармонической функцией и для определения yпр можно вос-
пользоваться методом комплексных амплитуд.
Для определения свободной составляющей yсв необходимо найти 
корней характеристического уравнения
a p |
a |
1 |
p |
1 a p a |
0 |
0 |
, |
(1.4) |
|
|
|
1 |
|
|
|
полученного из уравнения (1.3).
Когда все корни уравнения (1.4) простые (различные), свободная составляющая реакции цепи имеет вид
13
y |
св |
A e p1t |
A e p2t |
A e p t |
A |
e pit |
, |
(1.5) |
|
1 |
2 |
|
i |
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
т.е. каждому корню соответствует слагаемое свободной составляющей вида
y i |
A e pit , |
(1.6) |
св |
i |
|
где Ai - постоянная интегрирования. |
|
|
Если какой-либо корень |
рк характеристического уравнения |
|
(1.4) имеет кратность (корни одинаковые) n, то этому корню соответствует слагаемое свободной составляющей вида
y (k ) |
( A A t A t 2 |
A t n 1 )e pkt . |
|
св |
1 2 |
3 |
n |
1.2.1. Общая схема применения классического метода анализа переходных процессов для цепей первого порядка
Схема состоит из следующих процедур, которые далее конкретно раскрываются на примере RC цепи (рис.1.6).
1. Анализ цепи до коммутации. В результате этого анализа определяют токи индуктивностей и напряжения емкостей в момент времени, непосредственно предшествующий коммутации
t 0
.
2. Определение независимых начальных условий. Независимые начальные условия представляют собой токи индуктивностей и напряжения емкостей в момент времени ( t 0
). Независи-
мые начальные условия находят с помощью законов коммутации.
3. Составление дифференциального уравнения цепи после коммутации (при t 0 ). Дифференциальное уравнение цепи составляют используя компонентные уравнения для индуктив-
ности или емкости, т.е. u |
|
L |
di |
, |
i |
С |
du |
и законы Кирхго- |
L |
|
|
||||||
|
|
dt |
|
C |
|
dt |
||
|
|
|
|
|
|
|||
фа. |
|
|
|
|
|
|
|
|
14
4.Анализ установившегося процесса в цепи после коммутации
(при t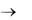 
). В результате анализа установившегося процесса в цепи после коммутации находят принужденную составляющую реакции цепи (частное решение дифференциального уравнения цепи).
5.Определение свободной составляющей реакции цепи. На этом этапе составляют характеристическое уравнение цепи, находят его корни и определяют общий вид свободной составляющей реакции цепи.
6.Нахождение общего вида реакции цепи. Общий вид реакции цепи (общее решение дифференциального уравнения цепи) находят путем суммирования свободной и принужденной составляющих реакции цепи.
7.Определение постоянных интегрирования ( Ai ). Постоянные
интегрирования определяются путем подстановки в общее решение значений токов или напряжений в начальный момент времени после коммутации при t 0 .
8. Определение реакции цепи, соответствующей заданным начальным условиям. Подставляя найденные постоянные интегрирования в общее решение дифференциального уравнения цепи после коммутации, находят его частное решение.
Пример 1.1. Определить переходной процесс в последовательной RC-цепи (рис.1.6), на которую воздействует напряжение e t
15
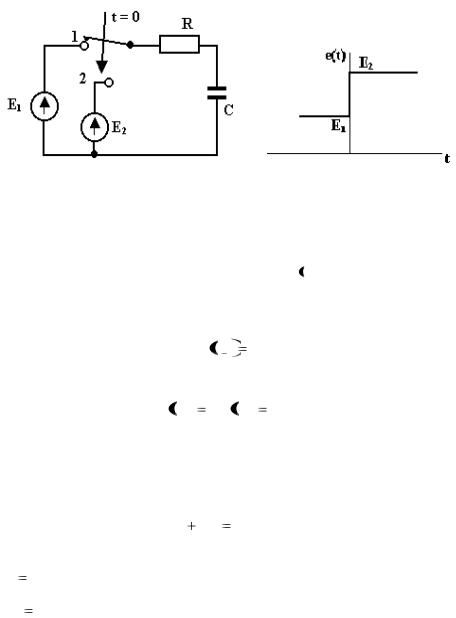
Рис.1.6. Последовательная RC цепь с графиком входного воздействия
Используя предыдущие рекомендации, выполняем следующие процедуры для определения напряжения uc t
.
1. Анализ цепи до коммутации. Очевидно, что в момент времени, непосредственно предшествовавший коммутации напряжения на емкости равнялось напряжению на зажимах источ-
ника энергии при t < 0, т.е. uC 0 |
E1. |
2. Определение независимых начальных условий. Независимое начальное условие выражается в виде
uC 0
uC 0
E1
Это единственное независимое начальное условие для схемы рис.1.6.
3. Составление дифференциального уравнения после комму-
тации. Второй закон Кирхгофа для схемы рис.1.6 записывается как
|
|
|
|
uR |
uC |
E2 . |
(1.7) |
|
Компонентное уравнение |
для |
этого случая берется |
в виде |
|||||
ic |
C |
duC |
. |
Подставляя его в (1.7), и используя зависимость |
||||
dt |
||||||||
|
|
|
|
|
|
|
||
uR |
ic R, получаем дифференциальное уравнение |
|
||||||
|
|
|
|
|
16 |
|
||
RC |
duc |
uc |
E2 . |
(1.8) |
|
dt |
|||||
|
|
|
|
4. Анализ установившегося процесса в цепи после коммутации при t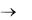 
. Для этого определяется принужденная составляющая процесса.
После коммутации в цепи (рис.1.6) при t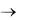 
получаем, что
uспр E2 ,
что соответствует заряду конденсатора С до напряжения Е2.
5. Определение свободной составляющей реакции цепи.
Характеристическое уравнение из (1.8) записывается в виде
RCp 1 0, где единственный корень p |
1/ RC |
|
|
1 |
, а |
||
|
|
|
|||||
|
|
1 |
|
|
|
|
|
RC - постоянная времени. Свободная составляющая пере- |
|||||||
ходного процесса получается в виде |
u |
св |
A e p1t |
A e t |
, ис- |
||
|
|
1 |
1 |
|
|
|
|
ходя из положений (1.5) и (1.6).
6. Нахождение общего вида реакции цепи. Это осуществляется через суммирование принужденного и свободного режимов цепи, т.е.
u |
c |
u |
спр |
u |
ссв |
, |
u |
c |
E |
2 |
A e t . |
|
|
|
|
|
|
1 |
7. Определение постоянной интегрирования. Для определения
постоянной интегрирования |
A1 |
|
используется |
независимое |
||||||||
начальное условие uc 0 |
uc |
0 |
|
E1. |
|
|
|
|
||||
Полагая |
в |
уравнении |
|
u |
c |
E |
2 |
A e t |
t |
0 |
и |
|
|
|
|
|
|
|
|
1 |
|
|
|
||
uc |
uc 0 |
|
E1 находим, |
|
что |
|
E1 |
E2 |
A1 , |
откуда |
||
A1 |
E1 |
E2 . |
|
|
|
|
|
|
|
|
|
|
8. Определение реакции цепи, соответствующей заданным начальным условиям. Подставляя найденную постоянную ин-
тегрирования |
A |
в |
общее |
решение |
u |
c |
E |
2 |
A e t / |
находим, |
||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
c |
Е |
2 |
E E |
2 |
e t / |
E |
2 |
|
E |
2 |
E e t / |
. (1.9) |
|
|
|
1 |
|
|
|
|
1 |
|
||||||
17
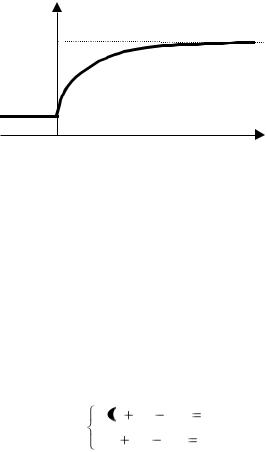
График переходного процесса в соответствии с (1.9) показан |
|
на рис.1.7. |
|
|
uc (t) |
E2 |
|
E1 |
|
0 |
t |
Рис.1.7. График переходного процесса |
|
1.2.2. Составление дифференциальных уравнений для разветвленных цепей
В том случае, когда электрическая цепь состоит из нескольких контуров, следует использовать для составления дифференциального уравнения цепи кроме закона Ома еще и законы Кирхгофа, учитывающие прохождение токов в контурах схемы.
Рассмотрим пример цепи первого порядка состоящей из двух контуров (рис.1.8).
Система уравнений для этого случая будет иметь следующий вид
i1 R R
i2 R uвх i2 R uL i1R 0.
18
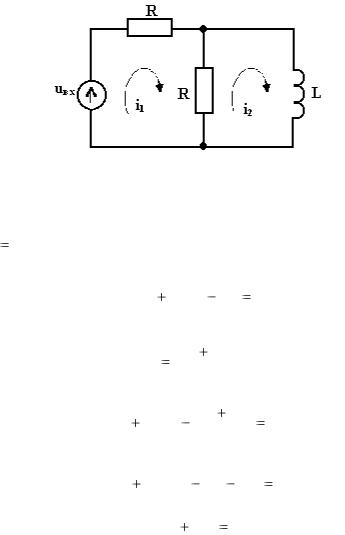
Рис.1.8. Электрическая цепь из двух контуров
Будем учитывать для решения системы уравнений также зависимость между током и напряжением на индуктивности, т.е. uL Ldi2 / dt. Подставляя это выражение во второе уравнение, получим, что
i2 R L |
di2 |
i1R 0. |
|
dt |
|||
|
|
Определив ток i1 из первого уравнения, т.е.
i1 |
uвх |
i2 R |
, |
|
2R |
||
|
|
|
и подставив его во второе уравнение, получим зависимость
i2 R L |
di2 |
|
uвх |
i2 R |
0. |
dt |
|
|
2 |
||
|
|
|
|
Осуществляя дальнейшие преобразования, получим, что
2i2 R 2L |
di2 |
uвх |
i2 R 0, |
|||
dt |
||||||
|
|
|
|
|||
2L |
di2 |
|
Ri2 |
uвх . |
||
dt |
||||||
|
|
|
||||
Последнее выражение и является дифференциальным уравнением цепи (рис.1.8), составленным относительно тока i2 . Его
решение осуществляется по правилам представленным ранее в п.1.2.
19
1.3. Переходные процессы в линейных цепях второго порядка сложности
Линейной цепью второго порядка сложности называется цепь, содержащая два независимых реактивных элемента.
Наиболее распространенными цепями второго порядка сложности являются цепи, содержащие R, L и С элементы, соединенные последовательно или параллельно.
Процессы в таких цепях описываются дифференциальным уравнением второго порядка, т.е.
a |
|
d 2 y |
a |
dy |
a |
|
y f t . |
|
2 dt |
|
|
|
|||||
|
2 |
1 dt |
|
0 |
|
|||
Если в цепях первого порядка свободные процессы описываются только экспоненциальными функциями времени, то в цепях второго порядка сложности возможны кроме этого и колебательные затухающие процессы, вызванные наличием резонансных контуров.
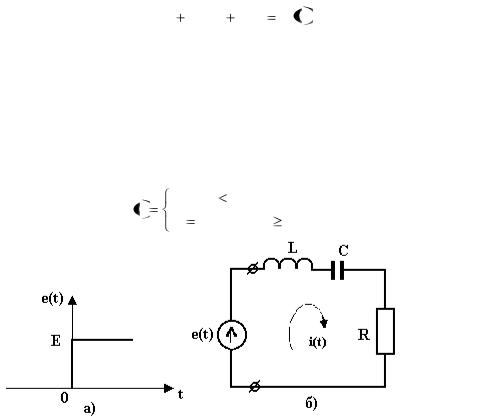
Рассмотрим пример определения переходного процесса после подключения к последовательной RLC цепи (рис.1.9) источника постоянного напряжения Е
e t |
0 при t 0 |
|
E const при t 0. |
||
|
Рис.1.9. График входного воздействия (а) и схема цепи (б)
20