Методическое пособие 657

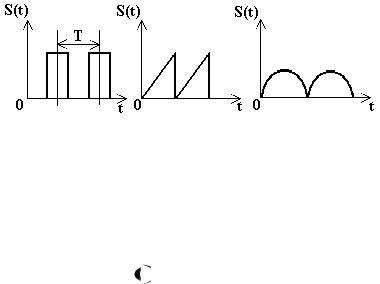
Как видно из рис. 4.35 результаты моделирования с помощью программы Workbench полностью совпадают с расчетными значениями (рис. 4.32, 4.33).

5.СПЕКТРЫ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ

5.1.Системы базисных функций

Наиболее распространенным электрическим колебанием является гармоническое. Для расчета цепей при таком воздействии существуют хорошо разработанные методы, например, метод комплексных амплитуд [1].

Однако, кроме гармонических колебаний в радиотехнических устройствах применяются колебания и других форм, из которых наиболее распространенными являются различные периодические импульсные сигналы (рис.5.1).

Рис.5.1. Периодические импульсные сигналы различной формы

Анализ электрических цепей при воздействии импульсных колебаний является довольно сложной задачей.

Эту процедуру можно упростить и свести ее к расчету цепи известными методами, если представить входное воздействие сложной формы S t (рис.5.1) в виде набора элементарных

колебаний и использовать принцип наложения, применяемый для линейных электрических цепей.

121

Для этого целесообразно представлять сигналы сложной формы в виде линейной комбинации простых функций (колебаний) i t

ний i t - разложением его по системе базисных функций. Если система базисных функций определена заранее, то воз-

a

Простейшим примером ортогональной системы функций, к которой можно применить (5.1) и (5.2), является тригонометрическая система:

Действительно, для (5.3) свойство (5.2) определяет, что

122

функций называется ортонормированной. Для такой системы справедливо равенство

В радиотехнике в качестве базисных функций наиболее часто используются гармонические функции (5.3), что объясняется рядом причин. Во-первых, гармоническое колебание, проходя

123

через линейные цепи, не искажается по форме, во-вторых, такие сигналы достаточно просто генерируются. И наконец, гармоническая функция является одной из самых удобных с математической точки зрения.

В последнее время в связи с развитием цифровых методов обработки сигналов стали использоваться и другие базисные функции: Уолша, Хаара, Лагера, Бесселя и т.п.

5.2. Определение спектра периодического сигнала

Рассмотрим теперь, как может быть представлен спектр периодического сигнала (колебания) S t S t nT , где T - пе-

риод, а функция сигнала удовлетворяет условиям Дихирле, т.е. имеет на всяком конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов.

Такой сигнал может быть представлен в виде набора гармони-

При использовании тригонометрического ряда (5.3) получим, что

Коэффициенты ряда (5.7), который называется рядом Фурье, определяются формулами:

2 T

a0 S t dt, (5.8) T

0

2 T

an S t cosn tdt, (5.9) T

0

124

Составляющие ряда (5.7) называются гармониками. Частота

следующие гармоники имеют более высокие частоты, соответственно 2 f1 , 3 f1 и т.д.

Ряд Фурье (5.7) может выражать заданную функцию S t с

любой требуемой точностью в зависимости от количества гармоник.

Чем выше требуемая точность, тем больше необходимо гармоник для формирования формы сигнала. На рис.5.2 показано образование прямоугольного импульса из суммы первой и третьей гармоник.

Рис.5.2. Формирование прямоугольного импульса из первой (n = 1) и третьей (n = 3) гармоник

125

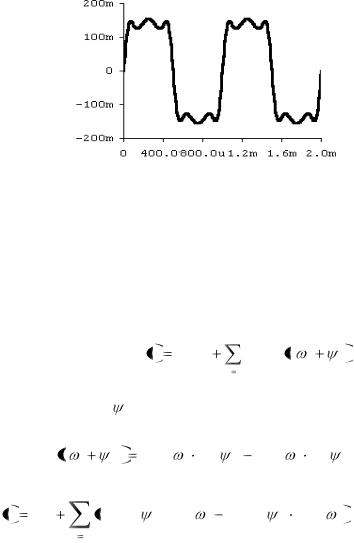
При большем количестве гармоник импульс приближается по форме к прямоугольному (рис.5.3).

Рис.5.3. Формирование прямоугольного импульса при большем числе гармоник

Ряд Фурье (5.7) можно представить в иной, более компактной форме записи

126

Сравнивая (5.7) с полученным выражением (5.12), определяем,

Спектр сигнала S t обычно представляется в виде графиков (рис.5.4) и называется линейчатым.

Рис.5.4. Спектр амплитуд (а) и спектр фаз (б) сигнала S t

Можно получить комплексную форму ряда Фурье, если в формуле (5.11) преобразовать выражение, стоящее под знаком суммы через формулу Эйлера

С учетом (5.14) ряд Фурье в комплексной форме записывается в виде

127

Определим теперь выражение для комплексной амплитуды An из (5.15), используя формулы:

График комплексного спектра по разложению (5.15) показан на рис.5.5.

Рис.5.5. График комплексного спектра амплитуд сигнала S t

128

Вид графика (рис.5.5) определяется тем, что в формуле (5.15) суммирование распространяется на области положительных и отрицательных значений частоты n . Это не свидетельствует о физическом существовании отрицательных частот при n 0 . Они являются лишь удобными в аналитическом отношении при расчетах.

5.3. Определение спектра непериодического сигнала

Рядом Фурье (5.11) могут быть представлены лишь периодические функции времени. Если взять одиночный импульс (непериодический), то можно ли его представить в виде спектральных составляющих?

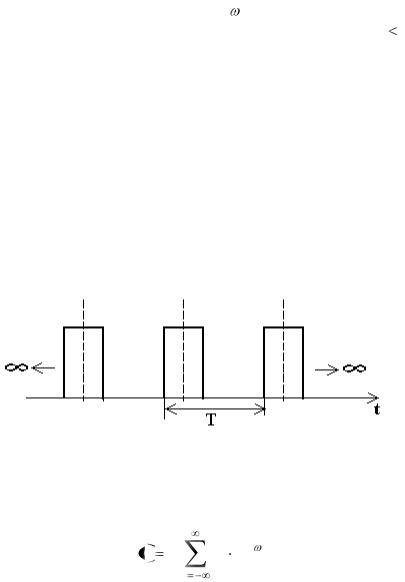
Будем считать, что такой импульс получен из периодической последовательности импульсов в результате удаления от него рядом расположенных импульсов при безграничном увеличении периода T (рис.5.6).

Рис.5.6. Получение одиночного импульса из периодической последовательности импульсов

Посмотрим теперь какие изменения произойдут при таком подходе в выражении (5.15) для ряда Фурье

Преобразуем эту формулу следующим образом

129

ставляет собой частотный интервал между составляющими

сгущается (рис.5.7).

Рис.5.7. Сокращение интервала между составляющими спектра при увеличении периода T

130