
Методическое пособие 657
.pdf
A p L a t |
a t e pt dt, |
0
где L – обозначение прямого преобразования Лапласа.
Это соответствие между оригиналом и изображением записывается как
A p : а t
: а t или a t
или a t : A p .
: A p .
Некоторые простейшие изображения функций представляются в виде следующих соотношений:
1. |
A : |
|
A |
, где |
A - постоянная величина; 2. 1 : |
1 |
; |
|||||||||||||||||
|
p |
p |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. e t |
: |
|
1 |
|
; 4 . 1 e t |
: |
1 |
|
1 |
|
|
|
|
|
|
; |
||||||||
|
p |
p |
|
|
p |
|
|
|
p p |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5. |
e j 0t |
: |
|
1 |
|
|
; 6. cos |
|
t |
: |
|
|
p |
|
|
; |
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
p j |
|
|
p 2 |
2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
7. |
sin |
0t |
: |
|
|
0 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p 2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подробные таблицы оригиналов и их изображений можно найти в справочнике [2].
Обратное преобразование Лапласа записывается в виде
|
|
0 |
j |
a t L-1 A p |
1 |
|
A p e pt dp, |
|
|
||
2 j |
|
||
|
|
|
0 |
j |
|
где комплексное число p S 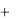 j
j - оператор преобразования
- оператор преобразования
Лапласа.
Однако напрямую этот интеграл не «берут», а поступают следующим образом. Если имеется возможность, то по полученному изображению находят оригинал в соответствии с таблицами, однако, если изображение такое, что оригинала в таблице нет, то используют так называемые формулы перехода от
31

изображения к оригиналу. Так, если изображение имеет вид
рациональной дроби |
|
F1 p |
, причем степень F |
|
ниже степени |
||||||||
|
|
|
|||||||||||
|
|
|
|
|
F2 p |
|
|
|
|
1 р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 р , а |
корни р1 , р2 , рк уравнения F2 р |
0 различны, |
то |
||||||||||
оригинал определяется выражением |
|
|
|
||||||||||
|
|
F1 р |
|
|
n |
|
F1 |
рk |
|
|
|
|
|
|
|
: |
|
|
e рk t , |
|
(1.23) |
||||||
|
|
F2 р |
|
F2 |
рk |
|
|
||||||
|
|
|
k 1 |
|
|
|
|
|
|
||||
где F1 р |
- значение функции |
F1 р , при р |
|
рk , а F2 рk |
- |
||||||||
значение производной F2 |
|
р после подстановки в нее вместо |
|||||||||||
р значений рk .
В случае, если знаменатель последнего выражения имеет один
корень, равный нулю, т.е. |
F2 р |
рF3 |
р , то оригинал нахо- |
||||||||||||
дится по формуле |
|
|
|
|
|
|
|
|
|
|
|||||
|
F1 |
р |
|
F1 р |
|
|
F1 |
0 |
|
n |
F1 |
pk |
|
|
|
|
: |
|
|
е |
pk t |
(1.24) |
|||||||||
|
F2 |
р |
рF3 р |
F3 |
0 |
|
k 1 pk F3 pk |
|
|||||||
|
|
|
|
|
|
||||||||||
где F1 0 |
и F3 0 |
- значения этих функций при р |
0. |
||||||||||||
В соответствующих справочниках,например [2], имеются формулы и для кратных корней уравнения F2 р 0
1.4.3. Некоторые основные свойства преобразования Лапласа
Эти свойства можно представить в виде следующих соотношений:
1.k : kр ;
2.ka t : kA р ;
: kA р ;
NN
3.ai t : Ai р , где ai t : Ai р ;
i 1 |
i 1 |
32

4. |
|
da t |
: |
pA р , если начальное значение a t равно нулю, |
||||
|
|
|||||||
|
dt |
|||||||
|
|
|
|
|
|
|
|
|
|
т.е. a 0 |
|
|
0 ; при a 0 |
0 получаем,что |
|||
|
|
da t |
: |
рA р |
a 0 ; |
|
||
|
|
|
|
|||||
|
|
dt |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
A р |
|
|
5. |
|
a t dt |
: |
|
при нижнем пределе 0, |
|||
|
р |
|||||||
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
t |
|
|
|
А p |
0 |
|
|
|
|
a t dt |
: |
|
a t dt, где 0 . |
|||
|
|
|
p |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
Если интеграл |
a t dt при t |
0 изменяется скачком, то нужно |
||||||
брать его значения справа от нуля, что и обозначено в верхнем пределе знаком 0+.
1.4.4. Операторные схемы замещения идеализированных двухполюсных элементов
По аналогии с комплексным сопротивлением Z j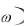 вводится понятие операторного сопротивления Z p . Также поступают и для проводимости, т.е. Y j
вводится понятие операторного сопротивления Z p . Также поступают и для проводимости, т.е. Y j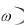 заменяется на Y p .
заменяется на Y p .
Операторным входным сопротивлением пассивного линейного двухполюсника называется отношение операторного напряжения на входе двухполюсника к операторному току при нулевых начальных условиях, т.е.
|
|
U р |
|
: |
|
||
Z |
р |
|
|
I р |
|
, где U р : u t ; I p |
: i t , |
а |
Y p |
1 |
- операторная проводимость. |
||||
|
|
|
|||||
|
|
Z p |
|||||
|
|
|
|
|
|
|
|
33

На практике, чтобы получить Z p  необходимо найти ком-
необходимо найти ком-
плексное |
сопротивление |
Z j |
и |
заменить |
|
j |
|
на |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
р j |
p , |
|
т.е. |
ZL |
j L |
Z p |
pL, |
Zс |
|
j |
C |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Z p |
|
, |
ZR |
R Z р |
R. |
|
|
|
|
|
|
|
рС |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь учитывается, |
что для оператора |
p S |
j |
величина |
||||||||
S0 при нулевых начальных условиях.
Втом случае, когда начальные условия ненулевые, эквива-
лентные операторные преобразования для конденсатора С и индуктивности L , будут другими, где простой заменой j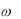 на
на
рпользоваться нельзя.
1.4.4.1. Эквивалентная операторная схема конденсатора при ненулевых начальных условиях
Напряжение на конденсаторе в общем случае определяется соотношением
|
|
|
1 |
t |
|
|
uс |
u с |
0 |
|
iс dt, |
(1.25) |
|
c |
||||||
|
|
|
|
|
0
где uс 0 - постоянная величина, отражающая начальный за-
ряд емкости.
Используя теорему интегрирования
t |
|
A |
|
|
|
|
a t dt |
: |
р |
, |
(1.26) |
||
|
|
|||||
р |
||||||
0 |
|
|
|
|||
|
|
|
|
|
||
а также свойство к : кр , выражение (1.25) записывается в ви-
де
U с |
p |
U |
с (0) |
1 |
I |
|
р . |
(1.27) |
|
|
р |
|
рС |
с |
|||||
|
|
|
|
|
|
|
|
||
34
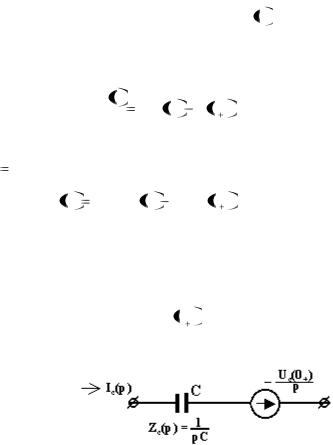
В соответствии с (1.27) теперь можно представить операторную схему замещения конденсатора при ненулевых начальных условиях, предварительно уточнив направление напряже-
ния у дополнительного источника |
U |
С |
0 |
в (1.27), учитываю- |
|
р |
|
||
|
|
|
|
щего начальные условия. Это можно осуществить с помощью теоремы дифференцирования
da t |
: |
рA р a 0 . |
(1.28) |
|
|
||||
dt |
||||
|
|
|
Применяя (1.28) к компонентному уравнению конденсатора
ic |
С |
duс |
|
, получим, что |
|
dt |
|
||||
|
|
|
|
||
|
|
IС |
р рСU С р СU С 0 . |
(1.29) |
|
В соответствии с (1.29) ток через конденсатор имеет две составляющие и вторая из них – отрицательна. В связи с этим на операторных схемах конденсатора ставят стрелку, совпадающую с направлением основного тока совместно с указанием
знака минус у значения |
U |
С |
0 |
(рис.1.13). |
|
|
р |
||
|
|
|
|
Рис.1.13. Операторная схема замещения конденсатора
Схему по рис.1.13 можно представить через обозначение конденсатора в виде операторного сопротивления (рис.1.14).
35
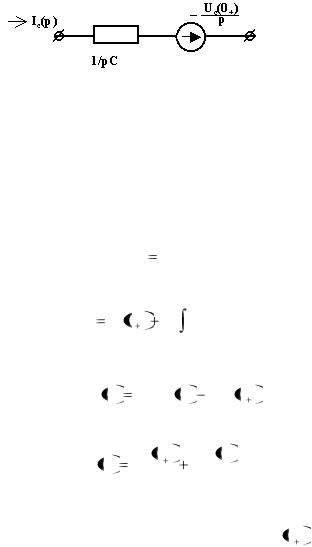
Рис. 1.14. Схема конденсатора в виде операторного сопротивления
1.4.4.2. Эквивалентная операторная схема индуктивности при ненулевых начальных условиях
Для индуктивности напряжение и ток выражаются соответственно соотношениями
uL |
L |
|
di |
|
(1.30) |
||
dt |
|||||||
|
|
|
|
||||
и |
|
|
|
|
|
|
|
|
|
1 t |
(1.31) |
||||
iL iL 0 |
|
|
|
uL dt. |
|||
|
|
|
|||||
|
|
L 0 |
|
||||
Применяя к (1.30) теорему дифференцирования (1.28) получим, что
U L p : pLI L p LI L 0 . |
(1.32) |
Используя теорему интегрирования (1.26), получим для (1.31)
I L |
p |
I L 0 |
U L |
p |
. |
(1.33) |
|
p |
|
pL |
|||||
|
|
|
|
|
|||
Из уравнения (1.32) видно, что в выражении напряжения на индуктивности появилась новая составляющая LI L 0 , опре-
деляемая как дополнительный источник напряжения, составляющая тока которого совпадает с основным током, о чем свидетельствует знак плюс у второго слагаемого в (1.33).
36
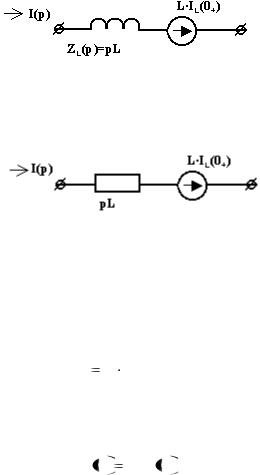
С учетом этого операторная схема для индуктивности при ненулевых начальных условиях может быть представлена как на рис.1.15.
Рис.1.15. Операторная схема индуктивности при ненулевых начальных условиях
Как и для конденсатора (рис.1.14) схему по рис.1.15, можно изобразить через операторное сопротивление (рис.1.16)
Рис.1.6. Схема индуктивности в виде операторного сопротивления
1.4.4.3. Эквивалентная операторная схема сопротивления
Для сопротивления напряжение и ток связаны между собой зависимостью закона Ома
uR R i. |
(1.34) |
Учитывая, что умножению функции времени на постоянное число соответствует умножение изображения функции на это же число, то для (1.34) получим, что
U R p RI R p . |
(1.35) |
В соответствии с (1.35) эквивалентная операторная схема сопротивления может быть представлена на рис.1.17.
37
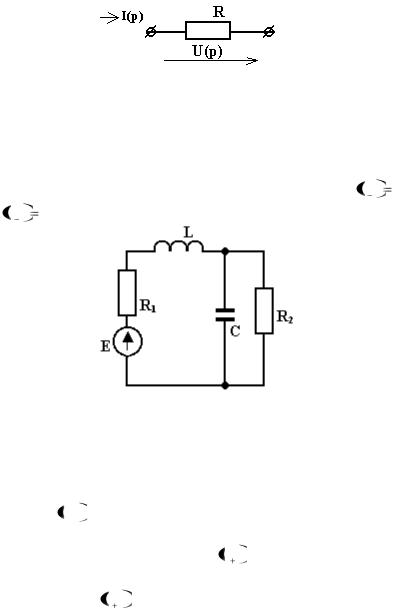
Рис.1.17. Эквивалентная операторная схема сопротивления
Пример 1.2. Приведем пример использования эквивалентных операторных преобразований для L, C и R на конкретной схеме.
Дана электрическая цепь (рис.1.18) и требуется начертить
операторную схему ее замещения, если uC 0 |
E0 , |
|
iL 0 |
I 0 . |
|
Рис.1.18. Схема электрической цепи
Для составления эквивалентной операторной схемы ненулевые начальные условия будем учитывать для индуктивности введением дополнительного источника э.д.с. равного по величине L  I 0
I 0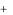 и по направлению совпадающего с положительным направлением тока, а для конденсатора введением
и по направлению совпадающего с положительным направлением тока, а для конденсатора введением
дополнительного источника |
U C |
0 |
и противоположно на- |
|
p |
||
|
|
|
|
правленного U C 0 . |
|
|
|
38
Так |
как в |
рассматриваемом примере iL 0 |
i 0 |
I 0 , а |
|
uc 0 |
uc |
0 |
E, то операторная схема цепи может быть |
||
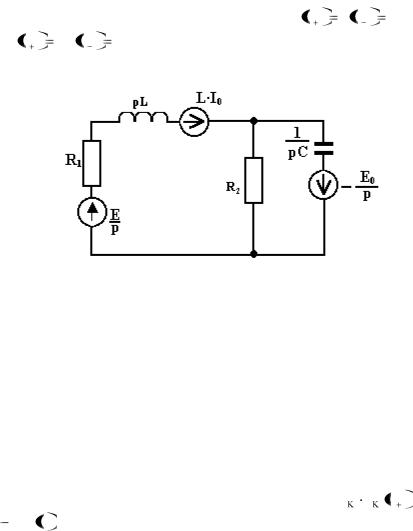
представлена в виде рис.1.19. |
|
|
|||
Рис.1.19. Эквивалентная операторная схема цепи
1.4.4.4. Основные этапы анализа переходных процессов операторным методом
Анализ переходных процессов осуществляют по этапам.
1.Анализ цепи до коммутации и определение независимых на-
чальных условий. Эта процедура выполняется так же, как и при использовании классического метода.
2.Составление операторной эквивалентной схемы цепи после коммутации. Ненулевые начальные условия учитываются
введением дополнительных источников э.д.с. L I 0 |
и |
U C 0 / p.
3. Составление уравнений электрического равновесия цепи в операторной форме. Система уравнений электрического равновесия цепи в операторной форме может быть сформирована любым методом, из ранее применяемых при расчетах электрических цепей, непосредственно по операторной схеме замещения.
39
4.Решение уравнений электрического равновесия цепи относительно изображений искомых токов и напряжений. Это может производиться любым из известных методов.
5.Определение оригиналов искомых токов и напряжений.
Производится путем применения таблиц обратного преобразования или формул перехода от изображения к оригиналу.
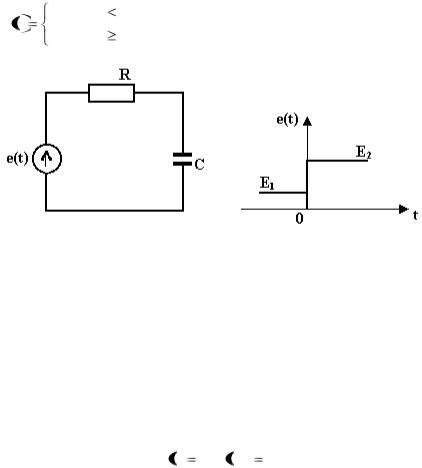
Пример 1.3. Для схемы, изображенной на рис.1.20, определить ток в цепи, используя операторный метод, если
e t |
E1 при t |
0 |
||
E2 |
при t |
0. |
||
|
||||
Рис.1.20. RC цепь с графиком входного воздействия
Представленная цепь аналогична той, которая рассматрива-
лась в примере 1.1, где применялся классический метод. Теперь требуется определить ток в цепи, используя операторный метод. Для этого будем применять рассмотренные ранее основные этапы анализа. С учетом их особенностей последовательность решения задачи будет следующей:
1. Осуществляем анализ цепи до коммутации и определяем независимые начальные условия, т.е.
U C 0 U C 0
U C 0 E1;
E1;
40
