
Методическое пособие 551
.pdf
Поскольку не зависит от r, то |
|
и уравнения Ла- |
|
||
гранжа свободной частицы имеют вид |
|
|
следовательно, |
|
|
Но является функцией только , |
|
|||
поэтому получаем |
. Таким образом, мы снова при- |
||
шли к закону инерции: в инерциальной системе отсчета свободное движение происходит с постоянной по величине и направлению скоростью.
Рассмотрим новую инерциальную систему отсчета, которая движется с бесконечно малой скоростью относительно исходной. Тогда, согласно закону сложения скоростей, в новой
системе отсчета скорость точки равна |
, а функция |
Лагранжа |
|
Разлагая это выражение в ряд и ограничиваясь членами первого порядка малости, получим
Согласно принципу относительности, законы движения в обеих системах отсчета должны быть одинаковы. Чтобы уравнения Лагранжа для функций L и L' были одинаковы, второе слагаемое в правой части выражения (4.21) должно быть полной производной по времени от некоторой функции координат и времени. Заметим, что полная производная от функции координат и времени должна линейно зависеть от скорости:
61
Отсюда заключаем, что величина не должна зависеть от
скорости, т.е. функция должна быть прямо пропорциональна
:
где m – постоянная, называемая массой материальной точки. Покажем теперь, что функция Лагранжа удовлетворяет
принципу относительности и в том случае, когда вторая система отсчета движется не с бесконечно малой, а некоторой конечной скоростью V относительно первой системы:
т.е. функции L и L' отличаются на полную производную функции координат и времени, поэтому соответствующие им уравнения движения будут эквивалентны.
Остается установить знак постоянной m, для этого будем исходить из принципа наименьшего действия, согласно которому на малых отрезках пути из точки 1 в точку 2 действие
имеет минимум. Поскольку при m < 0 действие могло бы неограниченно уменьшаться с увеличением , то есть не имело бы минимума, заключаем, что m > 0.
Рассмотрим теперь замкнутую систему взаимодействующих между собой точек. В этом случае к функции Лагранжа
62

должна быть добавлена функция координат точек, которую мы обозначим – U:
Как мы уже знаем, функция U является потенциальной энергией системы. Заметим, что U для замкнутой системы может зависеть только от расстояний между точками , поскольку только разности векторов остаются неизменными при переносе координатной системы, т.е. удовлетворяют принципу относительности. Если система не содержит связей, то в качестве обобщенных координат можно выбрать декартовы координаты, и уравнения Лагранжа (4.17) после подстановки функции Лагранжа (4.26) перейдут в уравнения второго закона Ньютона:
Задачи
4.1.Используя уравнение Эйлера-Лагранжа, показать, что кратчайшее расстояние между двумя точками на плоскости равно длине отрезка прямой, соединяющего эти точки.
4.2.Частица, начальная скорость которой равна нулю, движется под действием собственного веса по некоторой траектории, проходящей через две заданные точки. Показать, что кривая, движение вдоль которой от верхней точки до нижней происходит за минимальное время, представляет собой циклоиду с изломом в начальной точке (задача о брахистохроне, см. [1], п. 2.2).
63
§5. Законы сохранения и свойства симметрии
5.1.Интегралы движения
Пусть s – число степеней свободы, тогда для интегрирования уравнений Лагранжа, представляющих собой дифференциальные уравнения второго порядка, требуется задать 2s
начальных условий: s обобщенных координат |
и столько же |
|
обобщенных скоростей |
в момент времени t0. Тогда, решив |
|
систему уравнений Лагранжа, мы получим обобщенные координаты как функции времени, начальных координат и скоростей:
Продифференцировав эти равенства по времени, получим обобщенные скорости как функции тех же величин:
Решая (4.1) и (4.2) относительно начальных координат и скоростей, получим 2s уравнений вида
Такие функции координат и скоростей системы, которые во время движения остаются постоянными, называют интегралами движения (первыми интегралами уравнений движения).
Особенно важную роль играют интегралы движения, происхождение которых связано со свойствами симметрии пространства и времени (однородность и изотропность пространства, однородность времени, см. п. 1.3). Они обладают важным свойством аддитивности, которое позволяет делать на их основе (без интегрирования уравнений движения) ряд за-
64

ключений о состоянии тел после взаимодействия, если их состояние до взаимодействия известно. Для замкнутой механической системы существует семь таких аддитивных интегралов движения: полная энергия и по три компоненты векторов импульса и момента импульса. Хотя мы уже рассматривали ранее законы сохранения этих величин, мы получим их снова в рамках формализма Лагранжа, показав связь этих законов со свойствами симметрии механической системы1.
5.2. Обобщенный импульс. Циклические координаты
Для консервативной системы потенциальная энергия зависит только от координат частиц и не зависит от скоростей, поэтому мы можем записать
т.е. декартова составляющая импульса равна частной производной функции Лагранжа по соответствующей компоненте скорости. По аналогии, величину
называют обобщенным импульсом, соответствующим обобщенной координате .
1 Связь между симметрией функции Лагранжа и интегралами движения устанавливает имеющая общий характер теорема Нётер. Согласно этой теореме, для системы дифференциальных уравнений, являющихся уравнениями Эйлера-Лагранжа для некоторого вариационного принципа, из инвариантности вариационного функционала по отношению к - параметрической группе преобразований следует существование законов сохранения (см., например, [6], п.5; [9], §5).
65

Заметим, что для системы со стационарными голономными связями T является однородной квадратичной функцией
обобщенных скоростей, поэтому |
|
и уравнения Лагранжа |
|
(2.23) для такой системы можно переписать в виде, формально совпадающем со вторым законом Ньютона (1.13):
Для консервативной системы эти уравнения примут вид
Если функция Лагранжа не зависит явно от обобщенной координаты , то такую координату называют циклической. Для циклической координаты уравнение Лагранжа имеет вид
откуда следует следующая теорема о сохранении: обобщенный импульс , соответствующий циклической координате , остается постоянным, т.е. является интегралом движения.
5.3. Закон сохранения импульса и однородность пространства
Пусть обобщенная координата |
выбрана таким образом, |
|
что ее приращение |
описывает |
параллельный перенос |
(трансляцию) рассматриваемой консервативной системы как целого в некотором направлении (например, представляет собой одну из декартовых координат центра инерции системы). При параллельном переносе системы скорости ее точек не изменяются, поэтому кинетическая энергия системы T не зависит от и соответствующее уравнение Лагранжа имеет вид
66

или
Выясним физический смысл величин и , сопряженных выбранной указанным выше способом координате . Запишем выражение для обобщенной силы:
В нашем случае есть перемещение системы как целого в направлении некоторого единичного вектора n, при этом вектор будет равен разности радиус-векторов и для каждой i-й точки системы. По определению произ-
водной,
Следовательно, обобщенная сила представляет собой проекцию полной силы, приложенной к системе, на направление n:
Покажем теперь, что обобщенный импульс представляет собой проекцию полного импульса системы на направление n:
67

Уравнение (5.9), таким образом, представляет собой уравнение движения центра инерции системы в заданном направлении n.
|
Если координата является циклической, то |
и |
, т.е. мы пришли к закону сохранения импульса: если |
проекция действующей на систему полной силы на некоторое направление равна нулю, то проекция полного импульса системы на то же направление является интегралом движения.
Для замкнутой системы и сохраняющейся величиной будет вектор полного импульса системы, а координата , приращение которой определяет параллельный перенос системы как целого, будет циклической для любого направления переноса n. Заметим, что это обстоятельство следует также из свойства однородности пространства: законы движения при параллельном переносе замкнутой системы должны оставаться неизменными, следовательно, соответствующая такому переносу координата не может явно входить в функцию Лагранжа.
5.4.Закон сохранения момента импульса
иизотропность пространства
Выберем обобщенную координату |
таким образом, |
|
чтобы ее приращение |
соответствовало углу поворота сис- |
|
темы как целого вокруг некоторой оси, направление которой зададим единичным вектором (рис. 5.1.). По модулю скорости частиц при повороте системы не изменятся, поэтому кинетическая энергия T не зависит от и уравнение Лагранжа для этой координаты будет иметь такой же вид (5.10), как и для
68
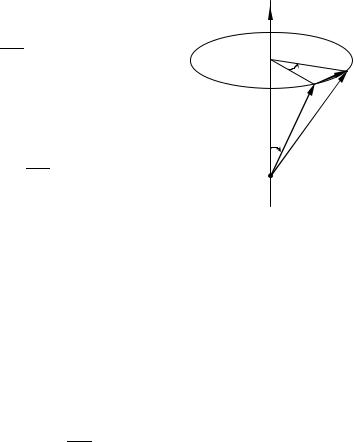
обобщенной координаты, определяющей параллельный перенос системы. Однако, в данном случае величины и будут иметь иной физический смысл. Выберем начало координат на оси вращения, тогда модули радиус-векторов точек при повороте системы не будут изменяться. Как видно из рис. 5.1, для бесконечно малого поворота
или
Учитывая это соотношение и взаимную ортогональность векторов , и , заключаем, что
После подстановки этого равенства в выражение для обоб- Рис. 5.1 щенной силы (5.13) получим
где N – вектор полного момента сил, действующих на данную систему. Таким образом, обобщенная сила представляет собой проекцию полного момента сил на ось вращения.
Подставим теперь соотношение (5.17) в выражение для обобщенного импульса:
69

где – вектор полного момента импульса системы. Таким образом, обобщенный импульс есть проекция полного момента импульса системы на ось вращения. Согласно (5.19), проекция момента импульса на некоторую ось z равна частной производной функции Лагранжа по , где – угол поворота вокруг оси z:
Если координата является циклической, то и Следовательно, мы получили закон сохранения момента импульса: если проекция полного момента сил, при-
ложенных к системе, на некоторое направление равна нулю, то проекция полного момента импульса на то же направление является интегралом движения. Вектор полного момента им-
пульса будет интегралом движения, если система замкнута: в этом случае в силу свойства изотропности пространства угловая координата qj будет циклической при любом выборе оси поворота.
Итак, мы показали, что законы сохранения импульса и момента импульса механической системы являются частными случаями теоремы о сохранении обобщенных импульсов, соответствующих циклическим координатам. Цикличность «трансляционной» обобщенной координаты, соответствующей параллельному переносу системы как целого вдоль некоторого направления, означает инвариантность системы (и, соответственно, ее функции Лагранжа) относительно такого переноса. Аналогично, цикличность «угловой» координаты, соответствующей повороту системы как целого, означает инвариантность системы относительно поворота вокруг данной оси.
Если система замкнута, то цикличность трансляционных и угловых координат следует из свойств симметрии (однород-
70
