
Методическое пособие 551
.pdfв каждой точке некоторой области пространства на матери-
альную точку действует определенная сила |
, то говорят, |
что в этой области задано векторное силовое поле. |
|
Интеграл (1.43) в общем случае зависит от пути, по которому перемещалась материальная точка. Если силовое поле таково, что работа A12 не зависит от траектории перемещения точки, то такая сила называется консервативной. Механические системы, в которых действуют только консервативные силы, также называют консервативными. Можно дать другое, эквивалентное определение: сила называется консервативной, если ее работа при перемещении материальной точки по замкнутой траектории равна нулю:
Очевидно, что силы трения не являются консервативны-
ми, поскольку для таких сил скалярное произведение |
все- |
гда отрицательно и условие (1.46) не будет выполнено. |
|
Поскольку работа консервативной силы зависит только от начального и конечного положения перемещаемой материальной точки, силовое поле такой силы можно характеризовать значением работы, производимой при перемещении из некоторой произвольно выбранной «нулевой точки» в данную точку пространства . Эту величину , имеющую размерность энергии, называют силовой функцией. Тогда работа A12 будет равна приращению силовой функции:
а элементарная работа dA определяется полным дифференциа-
лом функции |
: |
|
|
Введем функцию |
и найдем соотношение |
||
между вектором силы и скалярным полем |
: |
||
|
|
21 |
|

откуда заключаем, что
или, в векторной форме,
Таким образом, консервативную силу можно представить в виде взятого с обратным знаком градиента некоторой скалярной функции U(r). Такой переход от векторного силового
поля F(r), соответствующего трем скалярным функциям |
, |
||
, |
, к скалярному полю |
значительно упрощает |
|
рассмотрение консервативных сил. Направление вектора силы, как следует из (1.51), совпадает с направлением наибыстрейшего убывания поля U. Соотношение (1.51) часто записывают в виде
где под производной скалярной функции по вектору понимается вектор, компоненты которого равны производным от этой функции по соответствующим компонентам вектора.
Величину U называют потенциалом или потенциальной энергией. Консервативные силы, т.е. силы, удовлетворяющие условию (1.51), называют также потенциальными силами. Равенство (1.51) не изменится, если к U добавить произвольную постоянную (в пространстве) величину, таким образом, поло-
22

жение системы, при котором потенциальная энергия равна нулю, может быть выбрано произвольно.
Заметим, что поскольку , для потенциального силового поля
или
Равенства (1.53) или (1.54) представляют собой условие кон-
сервативности силы |
|
|
Если задано потенциальное поле |
, векторное поле |
|
находится из соотношения (1.51). Если, наоборот, извест- |
||
но векторное поле консервативной силы, |
то поле |
нахо- |
дится путем интегрирования: |
|
|
где C – произвольная постоянная.
Итак, работа консервативной (потенциальной) силы равна разности потенциальных энергий в начальном и конечном состояниях:
В то время как кинетическая энергия материальной точки определяется модулем ее скорости, т.е. представляет собой энергию движения, потенциальная энергия зависит от координат материальной точки и определяется ее взаимодействием с другими телами.
Величину E = T + U называют полной механической энер-
гией материальной точки. Из соотношений (1.45) и (1.56) заключаем, что
23

Таким образом, справедлива теорема о сохранении энер-
гии материальной точки: если силы, действующие на материальную точку, консервативные, то ее полная энергия T+U ос-
тается неизменной. В случае неконсервативных сил полная механическая энергия не сохраняется, она может переходить в другие виды энергии (например, в тепло).
1.7. Энергия системы материальных точек
Запишем работу всех внешних и внутренних сил при перемещении механической системы из начального состояния 1
вконечное состояние 2:
Сучетом уравнений движения (1.20), эту работу можно записать в виде
Таким образом, совершаемая внешними и внутренними силами работа равна разности между конечным и начальным значением кинетической энергии системы. Последняя опреде-
ляется как сумма кинетических энергий всех материальных точек:
Найдем соотношение между кинетическими энергиями T
24

и T', определенных относительно систем отсчета K и K', из которых вторая движется со скоростью V относительно первой:
или
Формула (1.62) представляет собой закон преобразования кинетической энергии при переходе от одной инерциальной системы отсчета к другой. Пусть в системе отсчета K' рассматриваемая механическая система покоится как целое, т.е.
, тогда V есть скорость центра инерции в системе K, и
Таким образом, кинетическая энергия системы складывается из кинетической энергии центра инерции, в предположении, что в нем сосредоточена вся масса системы, и из кинетической энергии движения материальных точек системы относительно центра инерции.
Предположим, что внутренние силы являются консервативными центральными силами, т.е. силы взаимодействия между i-й и j-й частицами Fij и Fji зависят только от расстояния между взаимодействующими частицами и направлены вдоль соединяющей эти частицы прямой. Пусть за
промежуток времени dt частица i сместилась на вектор , а частица j – на вектор . Работа, совершенная силами Fij и Fji с учетом третьего закона Ньютона будет равна
25
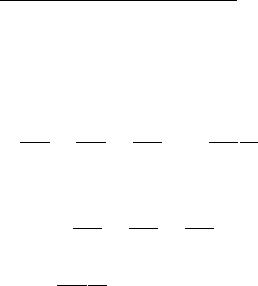
|
(1.64) |
Величина |
представляет собой переме- |
щение частицы i относительно частицы j, таким образом сумма элементарных работ пары сил Fij и Fji не зависит от выбора системы отсчета и равна элементарной работе, которую совершает сила, действующая на одну частицу, в системе отсчета, относительно которой вторая частица неподвижна.
Потенциал силы, действующей между двумя частицами j и i, является функцией расстояния между частицами и, следовательно, функцией координат обоих точек:
Запишем силу , с которой частица j действует на частицу i, считая, что частица j закреплена, а частица i движется в поле :
Аналогично получим силу :
Полный дифференциал от функции , взятый с обрат-
ным |
знаком, равен сумме элементарных работ сил |
и |
, |
|
или, |
что то же самое, работе силы |
на перемещении |
|
: |
|
26 |
|
|
|
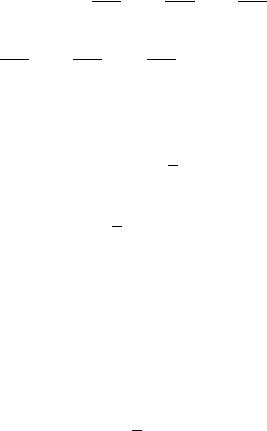
Запишем суммарную элементарную работу всех внутренних сил:
Наличие множителя ½ связано с тем, что при суммировании потенциалов Uji одна и та же пара индексов встречается дважды, и, в соответствии с (1.68), в отсутствии данного множителя мы получили бы удвоенную элементарную работу всех внутренних сил. Из соотношения (1.69) следует, что можно говорить о внутренней потенциальной энергии системы, понимая под ней сумму
Пусть внешнее силовое поле является стационарным и консервативным. Тогда каждая i-я частица системы движется
во внешнем потенциальном поле |
, при этом |
и
27

Сумму энергий всех частиц будем называть внешней потенциальной энергией системы:
Подставляя (1.70) и (1.73) в выражение (1.58), получим
где U – полная потенциальная энергия системы:
Из соотношений (1.59) и (1.74) следует, что
Таким образом, мы можем сформулировать теорему о со-
хранении энергии системы: если внутренние и внешние силы, действующие на точки механической системы, консервативны, то полная механическая энергия системы E=T+U остается постоянной.
Если внешнее поле является нестационарным, т.е. внешняя потенциальная энергия явно зависит не только от координат частиц, но и от времени, то полная энергия также будет функцией координат и времени и не остается постоянной. Закон сохранения механической энергии не выполняется также в случае, когда в системе действуют силы сопротивления (диссипативные силы). В этом случае изменение энергии при перемещении системы равно работе диссипативных сил:
28
т.е. будет происходить уменьшение («рассеивание») механической энергии системы.
Законы сохранения энергии, импульса и момента импульса играют важнейшую роль в механике. Эти три величины обладают важным свойством аддитивности – значение каждой из таких величин для механической системы равно сумме ее значений для отдельных частей системы. Законы сохранения таких аддитивных величин позволяют делать ряд общих заключений о протекании механических явлений, не прибегая к решению уравнений движения. Это во многих случаях значительно упрощает решение задач. Отметим также, что справедливость рассмотренных законов сохранения не ограничивается только классической механикой – они представляют собой универсальные законы природы. Позже мы получим законы сохранения энергии, импульса и момента импульса в рамках формализма Лагранжа и покажем, что они являются следствием свойств симметрии пространства и времени, упомянутых в п. 1.3.
Задачи
1.1. Человек ростом , двигаясь прямолинейно со скоростью ,
удаляется |
от фонаря, висящего на высоте . Определить скорость |
движения конца тени человека. |
|
1.2. Самолет летит горизонтально со скоростью |
600 км/ч |
|
на высоте |
6 км. Когда он пролетает над зенитной установкой, из |
|
орудия производится выстрел. Какова должна быть минимальная
начальная скорость |
снаряда и ее угол |
с горизонтом, чтобы сна- |
ряд попал в самолет? |
|
|
1.3. Автомобиль, трогаясь с места, движется с ускорением a1. |
||
После разгона до некоторой скорости |
он едет равномерно, после |
|
чего тормозит с ускорением a2 до остановки. Изобразите график зависимости скорости от времени. Какое время двигался автомобиль, если он прошел путь s?
1.4. Человек массы m = 60 кг перешел с носа на корму лодки.
29
На какое расстояние s сместится лодка, если ее длина равна l = 3 м, а |
||||||||||
масса M = 120 кг? |
|
|
|
|
|
|
|
|||
|
1.5. Тележка на «американских горках» начинает движение без |
|||||||||
начальной скорости на высоте h1 = 20 м над землей. Она спускается |
||||||||||
вниз до высоты h2 = 3 м и затем движется вверх до вершины сле- |
||||||||||
дующей горки, расположенной на высоте h3 = 15 м. Найти скорость |
||||||||||
тележки в нижней точке (на высоте h2) и на вершине высотой h3. |
||||||||||
Определить перегрузку, которую испытывает человек в тележке в |
||||||||||
нижней точке траектории, если радиус кривизны траектории в этой |
||||||||||
точке составляет = 10 м. Трением пренебречь. |
|
|
|
|
||||||
|
1.6. Дана система из двух частиц массами m1 и m2. В некоторой |
|||||||||
инерциальной системе отсчета скорости частиц равны |
и |
. Най- |
||||||||
ти импульсы этих частиц в системе центра инерции. |
|
|
|
|||||||
|
1.7. Частица, имеющая массу m и заряд e, влетает в однородное |
|||||||||
стационарное магнитное поле H со скоростью |
0, перпендикулярной |
|||||||||
направлению поля. Составить и проинтегрировать уравнения дви- |
||||||||||
жения, определить траекторию движения частицы ([13], задача 3). |
|
|||||||||
|
1.8. В некоторой области пространства одновременно имеются |
|||||||||
однородные и стационарные электрические и магнитные поля с век- |
||||||||||
торами E и H, угол между которыми равен |
. Частица с массой |
и |
||||||||
зарядом |
, имеющая начальную скорость |
, |
попадает в это про- |
|||||||
странство. Определить закон движения частицы ([13], задача 5). |
|
|||||||||
|
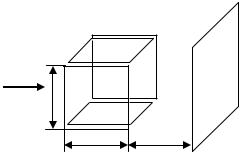
1.9. Пучок электронов влетает в пространство между двумя |
|||||||||
парами отклоняющих пластин (рис. 1.7). На вертикальные пластины |
||||||||||
подано переменное напряже- |
|
|
|
|
|
|||||
ние |
|
|
, а на гори- |
|
|
|
экран |
|||
зонтальные – |
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
||||
Перед влетом в это простран- |
|
|
|
|
|
|||||
ство |
все |
электроны |
имели |
|
|
|
|
|
||
скорость |
0, |
параллельную |
|
|
|
|
|
|||
всем пластинам. Длина пла- |
|
|
|
|
|
|||||
стин равна l, расстояние меж- |
|
|
|
|
|
|||||
ду параллельными пластина- |
|
|
|
|
|
|||||
ми равно d. Определить тра- |
|
|
|
|
|
|||||
екторию |
движения луча |
на |
|
|
|
|
|
|||
экране, |
расположенном |
на |
|
Рис. 1.7 |
|
|
|
|||
расстоянии l от пластин ([13], |
|
|
|
|
|
|||||
задача 8). |
|
|
|
|
|
|
|
|
|
|
30
