
Методическое пособие 551
.pdf§ 2. Обобщенные координаты. Принцип Даламбера-Лагранжа
2.1. Связи
При решении задач механики часто требуется учитывать связи, под которыми понимают любые ограничения на возможные движения точек системы. Физически связи реализуются различными направляющими, соединяющими стержнями, нитями, поверхностями, стенками и т.д.
Голономными называют связи, которые могут быть выражены уравнениями, в которых в качестве переменных фигурируют только координаты материальных точек и время, т.е. уравнениями вида
По зависимости от времени связи делят на стационарные
(склерономные) и нестационарные (реономные).
Если связь действует при любых положениях материальных точек системы, то такую связь называют удерживающей, в противном случае – неудерживающей.
Рассмотрим несколько простых примеров стационарных голономных связей:
а) материальная точка движется вдоль заданной кривой или по заданной поверхности. Уравнением связи будет уравнение кривой или поверхности;
б) плоский математический маятник с жестким стержнем длиной l (рис. 2.1, а), уравнение связи:
в) двойной плоский маятник (рис. 2.1, б), уравнения свя-
зей:
31

|
x |
x |
|
O |
|
O |
|
|
l |
l1 |
|
|
|
||
|
|||
|
M |
l2 |
|
|
|
|
|
A |
|
y |
|
|
|
||
y |
|
|
Рис. 2.1
г) движение твердого тела: точки тела всегда находятся на одинаковом расстоянии друг от друга, т.е. уравнения связей имеют вид
Пример нестационарной голономной связи: движение точки по поверхности сферы переменного радиуса. Уравнение связи при этом содержит время t:
В приведенных выше примерах связи были удерживающими. Если у плоского маятника, показанного на рис. 2.1а, заменить жесткий стержень на нить, то такая связь будет неудерживающей (нить может сминаться), она выражается неравенством
Подобные связи являются неголономными.
Связи, описываемые уравнениями (2.2)-(2.6), накладывают ограничения только на координаты материальных точек. Такие связи называют геометрическими. Связи, накладывающие ограничения не только на координаты, но и на скорости
32
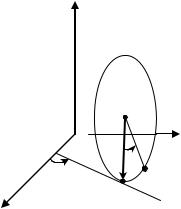
материальных точек, |
называют |
|
дифференциальными |
или кине- |
|
матическими. Рассмотрим в ка- |
|
|
честве примера диск, который |
|
|
катится по плоской поверхности |
|
|
без проскальзывания (рис. 2.2). |
|
|
Предположим для простоты, что |
C |
|
диск может располагаться толь- |
O |
|
|
ко вертикально. Тогда его поло- |
|
R |
|
|
|||
|
|
||
жение можно задать четырьмя |
|
|
|
|
|
|
|
параметрами, например, коорди- |
|
|
L |
натами x и y центра диска, углом |
|
|
P |
между осью Ox и касательной к ободу диска, проведенной в точке P соприкосновения диска с
поверхностью, и углом поворота диска вокруг своей оси. Если диск катится без проскальзывания, то связь «каче-
ния» накладывает следующее ограничение: скорость точки P соприкосновения диска с поверхностью будет равна нулю. Как мы покажем позже при рассмотрении кинематики твердого тела (п. 11), скорость точки P складывается из скорости поступательного движения диска (скорости центра диска) и линейной скорости вращательного движения этой точки, равной
,где - вектор угловой скорости (он равен по модулю
инаправлен вдоль оси вращения в соответствии с правилом правого винта), а R – вектор, проведенный из центра диска C в точку P. Таким образом, уравнение дифференциальной связи имеет вид:
Перейдем к проекциям на оси координат. Очевидно, что
, ,
Поэтому из (2.6) получим уравнения
33
или
Можно показать, что данные уравнения не могут быть проинтегрированы, поэтому их нельзя свести к выражению типа (2.1). Неинтегрируемые дифференциальные связи являются неголономными.
Итак, к голономным связям относятся удерживающие геометрические и интегрируемые дифференциальные связи.
В общем случае связи заставляют тела двигаться криволинейно. Такое движение всегда ускоренное, и эти ускорения можно связать с некоторыми силами, которые называют силами реакции связей. Силы, которые не зависят от связей, будем называть активными силами (примеры активных сил: сила тяжести, кулоновская сила и т.д.). Силы реакции связей возникают не сами по себе, а в результате действия активных сил. Силы реакции, в отличие от активных сил, изначально не известны (не заданы как функции координат и скоростей материальных точек системы) и должны определяться в ходе решения задачи.
Техническая механика рассматривает макроскопические системы, для которых характерно наличие связей (в том числе неголономных) в виде различных стержней, стенок и т.п., во многих случаях имеется необходимость учитывать силы трения (также, по сути, макроскопическое явление). С другой стороны, во многих разделах физики (физика элементарных частиц, атомная и молекулярная физики, физика твердого тела и т.д.) рассматриваются в основном механические системы, в которых связи либо отсутствуют, либо являются голономными. Мы в дальнейшем будем рассматривать, главным образом, механику голономных консервативных систем.
34
2.2. Обобщенные координаты
Пусть механическая система состоит из N материальных точек, и на движение этой системы наложено k голономных связей. Запишем систему уравнений движения:
В координатной форме (2.10) распадается на систему 3N дифференциальных уравнений. Наличие связей приводит к следующим проблемам: во-первых, силы содержат не только активные силы, но и силы реакции, которые изначально не заданы; во-вторых, ввиду наличия связей не все являются независимыми. Уравнения (2.9) тогда не являются независимыми, они должны быть дополнены k уравнениями голономных связей, с помощью которых необходимо исключить k координат и получить 3N-k независимых координат.
Для голономных систем можно вообще исключить из рассмотрения силы реакции и получить систему независимых уравнений движения при помощи введения т.н. обобщенных координат. Прежде чем мы приступим к изложению этого вопроса, рассмотрим несколько важных понятий.
Виртуальным (возможным) перемещением системы на-
зывают совокупность произвольных бесконечно малых изменений координат частиц системы ri, согласующихся с нало-
женными в данный |
момент времени |
уравнениями связи. |
Проекции вектора ri |
на оси координат xi, yi, zi называют |
|
вариациями координат. |
|
|
Виртуальное перемещение является возможным перемещением, но в действительности оно не происходит, его не следует путать с реальным перемещением за промежуток времени dt. Если дифференциал некоторой величины относится к изме-
35

нению этой величины вдоль траектории действительного движения и удовлетворяет уравнениям движения, то вариация отвечает переходу с траектории на другую, близкую к ней, она подчинена только связям.
Рассмотрим некоторую функцию координат и времени
Вариацией функции f бу-
дем называть приращение этой функции, обусловленное вариацией всех ее независимых переменных, кроме времени:
Запишем разложение функции |
|
в ряд Тейлора по степеням |
: |
Пренебрегая членами второго и высших порядков малости, получаем т.н. первую вариацию функции:
Таким образом, при условии , выражение для вариации функции (2.13) отличается от выражения для полного
дифференциала функции только отсутствием члена :
Числом степеней свободы механической системы называется число независимых между собой возможных (виртуальных) перемещений. Для случая голономной системы, число степеней свободы можно определить также как число неза-
36
висимых параметров, однозначно определяющих положение системы.
Обобщенными координатами системы называют независимые между собой параметры, число которых равно числу степеней свободы системы и которые полностью определя-
ют ее положение. Обобщенные координаты обычно обозначают буквой q.
Рассмотрим несколько примеров:
а) свободная материальная точка. Число степеней свободы s = 3, поскольку положение точки однозначно определяется тремя независимыми параметрами, например, декартовыми координатами x, y, z;
б) простой маятник (рис. 2.1, а). Декартовы координаты x и у точки M точки не являются независимыми, поскольку имеется связь, описываемая уравнением (2.2). Следовательно, такой маятник имеет одну степень свободы. В качестве обобщенной координаты q можно выбрать угол отклонения , или длину дуги AM, или площадь кругового сегмента OAM – любой из этих параметров однозначно определяет положение точки M;
в) двойной маятник (рис. 2.1, б) имеет две степени свободы, и в качестве обобщенных координат можно взять, например, углы и - очевидно, они не зависят друг от друга и полностью определяют положение системы.
Система из N точек в отсутствии связей имеет 3N независимых координат, т.е. 3N степеней свободы. Если на систему наложено k голономных связей, то число степеней свободы равно 3N-k. В случае голономных связей декартовы радиус-
векторы |
могут быть выражены через независимые |
|
обобщенные координаты |
. Уравнения вида |
|
37
называют уравнениями преобразования переменных ri к пере-
менным qi. Если связи стационарные, то уравнения (2.15) не будут явно содержать времени t.
Обобщенные координаты не следует рассматривать как некоторые ортогональные координаты, в их качестве могут быть выбраны любые величины, определяющие положение рассматриваемой системы. Это могут быть расстояния, углы, в ряде случаев – величины, имеющие размерность энергии или импульса и т.д. Различные обобщенные координаты системы могут иметь разную размерность. Например, в системе из двух точек, скрепленных жесткой связью, обобщенные координаты можно выбрать так: задать положение одной из точек в декартовых координатах, а положение второй точки задать шириной и долготой на шаре, в центре которого находится первая точка.
Поскольку обобщенные координаты независимы, на них не накладываются какие-либо связи – это одно из их преимуществ перед декартовыми координатами. Удобство использования обобщенных координат может быть связано также с симметрией конкретной задачи. Так, при рассмотрении движения точки в поле центральной силы (U = U(|r|), например, сила тяготения) даже в отсутствии связей гораздо удобнее использовать сферические координаты, нежели декартовы: в этом случае сила будет зависеть только от одной переменной r, что существенно упрощает решение уравнений движения.
2.3. Принцип Даламбера-Лагранжа
Рассмотрим систему из N частиц, на которую наложены идеальные голономные связи (под «идеальностью» подразумевается отсутствие трения). Наша цель состоит в том, чтобы исключить из рассмотрения силы реакции связей и получить уравнения движения в обобщенных координатах.
Обратимся сначала к случаю равновесия механической системы. В равновесии результирующие силы , действующие на каждую точку системы, равны нулю, и мы можем записать
38

Представим Fi в виде суммы активной силы |
и реакции |
связей fi: |
|
тогда получим |
|
Рассмотрим точку, на которую наложена идеальная (трение отсутствует) связь, заставляющая ее оставаться на заданной поверхности, определяемой уравнением связи. Тогда реакция связи будет перпендикулярной к этой поверхности, а виртуальное перемещение будет касательным к ней, следовательно, виртуальная работа реакции связи представляет собой работу сил трения в данной связи и будет равна нулю1.
В случае нескольких точек каждое слагаемое может и не обращаться в нуль, поскольку точки могут совершать работу друг над другом (например, если две точки скреплены жесткой связью, одна из них может потянуть за собой другую). Однако суммарная виртуальная работа реакции связей по прежнему будет равна нулю:
Таким образом, из (2.18) получаем условие равновесия системы, часто называемое принципом виртуальных переме-
1 Отметим, что мы можем не исключать из рассмотрения силы трения качения. Эти силы не совершают работу при виртуальном перемещении, согласующимся со связью качения, поскольку они приложены к точкам, находящимся в данный момент времени в состоянии покоя.
39

щений: виртуальная работа активных сил, приложенных к уравновешенной системе с голономными идеальными связями, равна нулю, т.е.
Перейдем теперь от случая равновесия к общему случаю движения системы. Будем трактовать уравнение движения
как уравнение равновесия i-й точки под действием реальной силы Fi и «силы инерции»1 – . Данный прием дает возможность формально свести динамику к статике. Вместо (2.18) тогда получим
Ограничимся снова случаем систем, для которых виртуальная работа связей равна нулю, тогда
Последнее равенство выражает принцип ДаламбераЛагранжа: движение системы происходит так, что в каждый момент времени сумма работ всех сил, включая и силы инерции, на виртуальных перемещениях равна нулю.
1 Не следует путать эти силы с силами инерции, возникновение которых связано с неинерциальностью системы отсчета.
40
