Методическое пособие 551

тельно, возможна только одна точка поворота, т.е. движение

где параметр p и эксцентриситет e определяются формулами (7.26), причем p будет отрицательным. При это уравнение описывает дальнюю от фокуса ветвь гиперболы (см. рис.

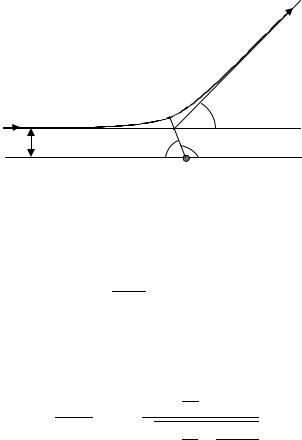
ставлен случай отталкивающего поля). Пусть частица движется к центру из бесконечности со скоростью . По мере приближения к центру траектория частицы будет отклоняться от начальной прямой, затем, при удалении частицы от центра действующее поле уменьшится настолько, что траекторию можно снова считать прямолинейной. Угол между начальным и конечным направлениями движения называют углом рассеяния. Расстояние b от начальной прямой, по которой движется частица, до силового центра называют прицельным расстоянием.

Как мы показали ранее (см. п. 7.1), траектория частицы будет симметрична относительно прямой, проведенной из центра поля в ближайшую точку орбиты (прямая OA на рис. 7.9). Таким образом, обе асимптоты орбиты образуют с указанной прямой одинаковый угол . Как видно из рис. 7.9, этот угол связан с углом рассеяния соотношением

91

стве имеют дело с потоками частиц, падающих с одинаковой скоростью на мишень. Рассеянные частицы регистрируются детектором, расположенном на достаточно большом расстоянии l от мишени. Во входное отверстие детектора попадут частицы, траектории которых после рассеяния лежат в преде-

дет пропорционально плотности падающего потока n, определяемой как число частиц, проходящих в единицу времени через единицу площади поперечного сечения исходного пучка. Поэтому вместо dN удобнее использовать отношение

которое не зависит от плотности падающего пучка (параметра эксперимента). Величина имеет размерность площади, ее называют дифференциальным эффективным сечением рассея-

ния. Она характеризует вероятность рассеяния частиц потока в телесный угол около заданного угла рассеяния .

Будем считать, что повторными соударениями частиц с рассеивающими центрами можно пренебречь (мишень достаточно тонкая), тогда описанный выше процесс рассеяния сводится к задаче об отклонении частиц в потенциальном поле

93

Эта формула выражает зависимость эффективного сечения рассеяния от угла рассеяния и прицельного параметра . По-

сам процесс рассеяния.

7.4. Формула Резерфорда

Если аналитический вид уравнения орбиты известен, то непосредственно из него можно найти зависимость между углом рассеяния и прицельным расстоянием. В качестве примера рассмотрим рассеяние частиц в отталкивающем кулоновском

поле ( , создаваемом неподвижным зарядом. Уравнением траектории будет уравнение гиперболы (7.37):

Угол можно найти, либо вычислив интеграл (7.41), либо воспользовавшись уже найденным уравне-

95

откуда находим

Соотношение (7.50) проблематично проверить в описанном ранее эксперименте, что связано с трудностями непосредственного измерения прицельного расстояния . Зато экспериментально можно определить дифференциальное эффективное сечение . Подставив в (7.45), получим

Легко показать, что данная формула справедлива и для притягивающего кулоновского поля.

Соотношение (7.51), называемое формулой Резерфорда, было получено Резерфордом для рассеяния быстрых альфачастиц (имеющих заряд +2e) на атомных ядрах. Как следует из

(7.51),

Постоянство левой части в (7.52) было проверено экспериментально, что подтвердило предположение Резерфорда о том, что рассеяние -частиц на большие углы связано с их кулоновским взаимодействием с атомными ядрами, имеющими положительный заряд .

будет интегралом движения. Показать также, что этот вектор (вектор Лапласа) направлен из центра поля в точку перигелия орбиты

[см. [2], §15 и [4], п. 3.3].

96

7.2. Найти вид центрального поля, в котором частица может двигаться по гиперболической спирали ([14], задача

2.31).

7.3. Определить траекторию движения частицы в поле

нутости траектории ([12], задача 2.5).

§8. Малые колебания

8.1.Свободные колебания системы с одной

степенью свободы

Важным классом движений механических систем являются малые колебания около положений равновесия. Как мы показали ранее, для системы с одной степенью свободы любое финитное движение является колебательным. Предположим, что такая система имеет положение устойчивого равновесия, т.е. имеется некоторое значение обобщенной координаты , при котором потенциальная энергия системы U(q) принимает минимальное значение. Запишем условия минимума :

В этом случае при отклонении от положения равновесия возникающая обобщенная сила будет стремиться вернуть систему в это положение.

Согласно формуле (6.2), функция Лагранжа системы с одной степенью свободы имеет вид

97

Разложим оба входящих в эту функцию члена (кинетическую и потенциальную энергию) в ряд по степеням :

лу условий (8.1). Предполагая, что отклонение от положения равновесия мало, в разложении кинетической и потенциальной энергий оставим только первые неисчезающие члены, тогда

или, введя обозначения

Систему, характеризуемую такой функцией Лагранжа,

называют гармоническим осциллятором. Соответствующее уравнение Лагранжа имеет вид линейного однородного дифференциального уравнения

которое совпадает с уравнением движения материальной точ-

98

где введено обозначение

Общее решение уравнения (8.8) описывает гармоническое колебательное движение, его можно записать в разных формах:

фициенты в (8.10) – (8.12) связаны соотношениями

и

Величину называют собственной частотой колебаний осциллятора, она является основной характеристикой колеба-

99

ний, не зависящей от начальных условий (последнее справедливо только для малых колебаний, когда ).

Определим энергию малых колебаний, подставляя в общее выражение для энергии формулу (8.11):

т.е. энергия пропорциональна квадрату амплитуды колебаний.

8.2. Вынужденные колебания

Пусть на систему, совершающую одномерные колебания, действует достаточно слабое (чтобы колебания оставались малыми) переменное внешнее поле . Колебания в этом случае называют вынужденными. Разложив внешнее поле в ряд по степеням x, получим

где величина , представляющая собой некото-

рую функцию времени, есть внешняя обобщенная сила, действующая на систему в положении равновесия.

Функция Лагранжа рассматриваемой системы отличается от функции (8.6) рассмотренного ранее случая свободных одномерных колебаний дополнительным членом :

Здесь мы отбросили величину , поскольку она зависит только от времени и, очевидно, может быть записана в виде полной производной по времени от некоторой другой функции времени. Уравнение движения, соответствующее такой функции Лагранжа, имеет вид

100