Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

очевидно,електронакож

E0

òî

реалiзувиплива¹,. суперпозицiйнийКоли ми запуска¹мостанв гру обидва протони,

З умов симетрi¨

ψ =ùîC1ψ1 + C2ψ2.

а з умови нормування

|C1|2 = |C2|2,

2

2

= 1.

|C1|

+ |C2|

Iз цих рiвнянь, обмежуючись дiйсними розв'язками, знаходимо

C1

1

1

= √2 ,

C2 = ±√2 .

ештдварозв'язкiв, вiдповiäíо до пункту

Такимзауваженьчином,домипринципуотрима¹-

мосуперпозицi¨, опè:сують той самий стан. 5◦

1

ψI = √

(ψ1

+ ψ2),

2

1

ßêùî

ψII =

√

(ψ1

− ψ2).

ψI

2

ó¨õíi

âèïëèâà¹,

виявля¹ться,Ω щочастотавiдповiднiперескокiвзначенняелектронаенерi¨ (дивмiж.риспротонами,.12) то

EI = E0 − ~Ω

Величину

EII = E0 + ~Ω.

плярний

ψI

тонамийон водню. З умов симетрi¨. У цьому станiщо посерединiма¹момолмiжку

âàí

електроназв'язанийнiй.

√

йм вiрнiс ь переб

ψ1

= ψ2

Ó öié òî÷öi

ψI = 2ψ1

ó ñòàíi

|ψI|

2

= 2|ψ1

2 максимальною. Оòæå, åëåê-

|

екранума¹моться,

ворюючизаряди. У резульнаходитьсаанпрояHпереважноони,посерединiхочмiжслабо, отонамиалепритягуй

ñòàíi

2+ з виграшем енер i¨ величиноþ A. Ó

62

ψII для точки, що лежить

мiж протонами,

системсильних.принципомвз¹мо

ä é ßêAведемо.приклМа¹мообмiнденерзв'язоксистемi¨ мезонамипримiждвоутвореннiпринципомзв'язаногоанамисуперпозицi¨бiльнихвтеорi¨

-

ану. Етиленприводитьуклонiв- . по глянемодоядрi,мiжмоленуклонами,ак улустанужобмiнетиленуйщоутворелюоприводитьCаминяадромiждо

нiвкваркз 'яз.Прами,ногокладякий3

π

вiзьмемодвiйнимкiв,протилежноакзванийзв'язêом (див. риссуперпозицi¨,.13)рухливимH. якiй,

атомиОдèвнглецюiзподвiйнихзв'язанiзв'я

2

4

ямленимизок,й, ¹

iíàìè.

Саменьомуцей ¹зв'язокдваелектрони,й

до увагинапрπ.-çâ'Iíø

нассильнонецiкавитимеронно¨з'язу¹вза¹мо. Мидi¨.акЯкщотут,жненабудемопоглядубратиïîìiñòèòнцдо увагипу-зв'язок,еекти щомi

желек

σ

iн можункцi¹юрозташув

ãî

Насправдiîþ

омадинвуглецюелек

òî

зтрон,хвиль

ïåðø

тись абоπ-зв'язокбiля

¹þ

ψ1 ðåàëiçóб бiля другого з хвильовою ункцi-

ψ2.

¹ обидвi можливостi дночасно,63

спiнамив падкуйрiвеньреалiзу¹тьсÿ

сiдають ен

EI

òà

EII

ψI

ψII

суперпозицiйнийелектрониан,олипротилежнинаенер.Iвцьетичу-

. ÒóòEI = E0 − A

äâà

ç

ìè

E0 åíåð iÿ, ùî

iäïîâiä ¹

íàì ψ1

, ψ2; A = ~Ω,

K′. Вони пов'язанi перетвореннями €àëiëåÿ

,

величиниψ′ = C exp

−~ E′t′

+

~ p′r′

нештрихованi

належатiü äî ñèñò ìè

K, штрихованi до

i вiдповiдними

перетвореннями для iмпульсу та енер i¨:

t = t′,

r

= r′ + vt′

p = p′ + mv,

E = E′ + vp′

+

mv2

Легко показати, що

.

2

äå àçà

ψ = eiδ ψ′,

mv

масамиЯкщо ми ма¹мо лiнiйну супеδ = ðïîçèöiþ(r + r′ñòàíiâ).

частинок iз рiзними

2~

твiдлiкусистемi вiдлiку

K

,

m1

m2

то в системi

ψ = C1ψ1 + C2ψ2,

K′

iδ1

ψ1′ + C2e

δ2

ψ2′,

ψ′ = C1e

iндек суперечитьвеливiдрiзнятимутьс

Îòæå,

δ1

à δ2 позначають рiзнi маси у виразi для δ.

â

ùî

нерелятивiстськiйлише азовим множникомсованаумо

частинкиψ ψ′

-

è, Óà церелятивiстськiйпринциповiтеорi¨акаперетвоорi¨супрпозицiя€величинаалiлеяможливаiзично.Тимiкрiзнiтомучином,стащо.

величмас

m1 = m2; ÿêùî æ m1

вiдносностiто

ψ′

= m2,

ψ

6

æå,µприiмпульсуперех привiд ¹ скаля

Лоренца4-¹векторiвiнварi

анкоордоюèíà. Î pµx

= Et − pr = inv

нименняхдобутком

òåìóäà êîâî¨

àçè.

Як приклад ако¨ суперпозицi¨ можна навестибезсисдо-

K äî K′ óíêöiÿ ψ = ψ′

K0

мезонiв, якi ¹ суперпозицiйним станом K0

K0

5

арчукK0

I. Î. Âàê

L

65S

ê

т м, що в розпадах довгоживучого

10−6

eV). Приклад цi

мезонiв, що мають рiз

i ìàñè (

m

3.6

òåîðiÿ

· 0

мезона на π

+

+ π−

0

0

порушен( -канал)я

KL

ма¹мо ¹диний поки що спосте

æó

осциляцiяпадокмезони

2π

íèé

à π

+ π

електронн.1/3Припуска¹ться,вiдней.Друîãîрино,ийнейтрщоприкладщовщоðåмагно¹ста¹

öiéЗемлiприблиз-iнварiантностiнаСокiлькiстьаницi

нейтрино:

ниру¹тьсце нейтриноциклiвнаЗемлi,сонячнихядернихцесуперпозистановитьреакCP

мю нногонейтрино

νe,

нулевiрення

νµ

ау-нейтрино

ντ

-

динщотип¨хнiнейтрино,вiдбуваютьсямасиспокоюнаприклад,шляхувза¹мнiнедорiвнюютьвiдперетвоСонця

нейтрино,заадумови,ах)¹

ðå¹ñòðó

(особлив. Приладйого

ЗемлiНайбхнiриментатпоеккiвд

νe

спериментувсiйУзЗемлi,овiдь1998льшийре¹страцi¨пiдîвверхнiногамироцiнiжекспериментiшляхпростпитаннятi,атмпроекщодять.спериментхсЯкщодятьери,ейтриннихгрупиоротшийхнародждятьнейтринейтрино,тоатораяпонськихíàðîз шляхбудьосциляцiй.дженiЗвiдсинароджуютьсянар-вяккутовадовияватмосамериканськихджгонадвиплива¹,детектзнайшло,iíзалежнiстьголовоюшогоерiдруграЗемлiрiвномiрнощнапрзда¹ться,îгоякщо.поверекспе.ямкубокуIдеяiзи¹--.

акi осциляцi¨, то повинна спостерiг тись

êiëü-

частинки

точки 1

2 (ä

â. ðèñ. 14).

експеримент.

î

нейтрино. Саме це

Приклад 5. Перехiд до

механiки. озглянемо рух

Згiднозаре¹строванихпринципдом

класично¨цi¨, амплiтуда ймовiрностi по-

трапляння частинки з

точкисуперпоз1 точку 2

дохлучаютьТутдупiдсумовуванняпоK(2точкувнiй1)

амплiтуда ймовiрн стi переходу

.

ïî ïåâíié òðà¹êòîði¨

X

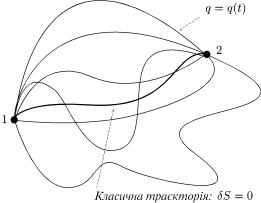
q = q(t)

тра¹кторi¨1зточкоювiдбува¹тьс2.Виявля¹тьсзавсiмая,тра¹кторiями,щоампiтудащопереспо

~

2

iS/

винувЦеточкивпершцю2,åiдеюзауваживвипробовуючиP.ФейнманП.А. Мвсi.Отже,.Дiрак,можливiдечàстинкосттра¹кторi¨,аточнопотрапля¹встановивцеасичнатойзточкисамийроздiя1-.

66

e

S = R1 L dt

ис. 14. Можливi тра¹кторi¨ руху частинки.

äíié

ðà

Чому ж у класичнiй механiцi частинк

ðóõà¹òüñÿ ïî

¹кторi¨? Ми ж це зна¹мо i щодня спостерiга¹мо вiзуально! У я

òîí-

у класи

нiй механiцi

10−27 ã

ñì

2

/ñåê,

à äiÿ

кiсть поляга¹ в тому, що стала Планксправу~

, актично ми

ìà¹ìîñì2

з прикла

ом цеiзично¨дуже

áâåзмежлик ÷îñòièñëî,

S 1

·

27

ã ·

/сек, тобто S/~ 10

÷îþ óìiíóкцi¹юя при переходi вiд

äíi¹¨ òðà¹êòîði¨øâèiS/~ äî äàþi шо¨,¹кторi¨сцпричомулюю-

S/~ → ∞. Òîìó óíêöiÿ e

ë øå

q˜знака= q+δq, що ¹ безмежно близькою до тр

ðà¹êòîðiÿ,q äà¹

òðà¹êòîðié ó

eiδS/~ àìïëiòóäè. Ó ðåçó ü àòi,

åñêè ñóñiäíiõ

що визнач ¹тьсяK(2,ç1)умовивза¹

гасяться . ™ лише

äíå

варiацiйнийзнак сàìå òîìó, ùî

δS = 0äi¨,ñóñiäè ÿêî¨ íå

ü öi¹¨ çìi

Всесвiтуä

либшо¨озглянемопуНехайщо.найменшо¨Такимкласиiнше,симетрiрух÷ÿêíi

ном,електрона¨вняння.ПМабуть,ма¹моиклад. рухувзв'язокцiпринципийонному6.частинкиП принципуляроннайменшкрсамièтст, ¨¨екситони,собоюлiуï¨.(наприклад,ерпозицi¨тиУ

δS = 0

ì¹оваальнанаслiдкамякогомагнониδSòòðà¹êòîðiÿ=випливаютьпрNaCl)0. íöã

-

хвильова ункцiя електрона на йонi з номером

ψn

5*

n. åàëiçó¹òüñÿ67

поляронектронплюсумолеку. поляризоолектилярномуâiзу¹тьсяанакристалiним йонамикристалiчна(типу.OТака ратка,квазiчастназива¹нка,

електроньсяобтоНехай

ψ = C1ψ1

+ C2ψ2 + · · · + Cnψn + · · · ,

ла пiд мером

уперпозицiйною2) збудж

молеку

диполь, стандипольно¨якопису¹ться хвильовою умандруêöi¹þ

УнаслiдоктомудномуОсновзаписаноюнапр.стий станперевернутиямвищеякоговласн.еромагнiтногоопису¹тьсяТакийхмагнiтнихзбудженийвза¹модi¨акожкристаламоментiвцеñ анзбудженнявiдповiдкристатомiвала¹називають.орi¹нтЯкщоункцi¹ацi¨по-.

вексит¹ю,кристалу,

n

ψn

òüñÿ ñòàí

ψn,

ðåàëiçó¹-

суперпозицiйнийψ, ùî ¹перебуваннялiмагнонiйню

ñòàíiâ ψ1,

ψ2, . . . . Öå

мiвнiй.Внаслiдокводнюж(ззнаходитисьсiхцьгоможливихенерiяäногоможстанiвабо, якмолекулибуватизiншогома¹дванасбокузначення:цiкавлятьпiрамiдиплощини.Азотсамеато-

öi)

3

ймовiрностей

E0 − A

E0 + A

, äå

A

îáìiííà

р iя. Причому амплiтуди

C1

,

C2

бува¹ вiдповiдно станах

òîãî, ùî àçîò

çàлежать вiд часу

ψ1, ψ2,

C1 =

1

e−

i

(E0−A)t +

1

e−

i

(E0+A)t,

~

~

2

2

1

e−

i

1

e−

i

а самi ймовiрностiC2 =

~

(E0

−A)t −

~

(E0+A)t,

2

2

|C1|2 = cos2 Ωt,

68

|C2|2 = sin2 Ωt,

ψ2

. Якщо в момент

t = 0

атом азотусистемах¹уанi

ψ1

, òî ÷å åç

÷àñ

вiн проберетьсвiдбуваютьс ан

T = π/(2Ω)

ψ2

ÿ

.

Такi ж перетворе ня

тоюнийдозвучанремклади,зонiв;iнструментвiдомийвисокихЦiкавоцеякiя:зичоливаньвонаакнавестимигармонiкедолiко¨жрозгля(високо¨акустрибкомстосу¹тьсяструнистикиприклад.íВиявля¹тьсулиак.зостi),Скрипкìзванийвищеайжеiню¹тьсяявищапроблеми.якiйя,збiга¹тьс

0

0

-

придоб-месаое

донсноюнизьких,¹iзики,тiднама¹частоосновстiйканота

армонiцi

вовчийбиттащоважкзагрупасонячнихнатембромявищезтоцiйкласично¨надатиiзструментрезон.вовчiйТобтотривале

нейтриноK - а K

рпусу. Енер iя пр

цьому

биття перех дить вiд

êiëüêè

до орпусу (с руна звучитьчастотоюдi на другiй

ñì ÷îê ðóõà¹òüñÿ)

íàâ àêè. Öå

експеримент

äî ëiäèâ

iзик Ч. аман (1918 р.), спостерiгаючи

альнодно-

струнича но колiндiйськийвання струни т корпусу8.

яко¨ орми врештi-решт

вдобротноголення

âанняпiзнаннiприво

òîãî,

Ÿ 4. Пар докси квантово¨ механiки

Велику роль

мiкросвiту мали дискусi¨ мiж учени-

розумiння квантово¨

åõàíi

è, íà ÿêå íàñ

штовха¹

ми, якi створили ква тову теорiю або

важливу р ль у

¨¨ розвитку. Кожен

цих великих людейвiдiгралитак не досягнув того

п всякденний дос iд. Вони по-рiзному висловлювали сво¹ незадо

набула

квантова

мех нiк . Цi дискусi¨ породжували рiзнi п радок-

тут лише триздивубагатьатмосх парадоксiв.ери,

î¨ íå ïiлюстрацi¨скають

свiтла, нi звуку,Всерединiтьсзнах я кiт. У скринь

ñè.

Äëÿ

äó

якiй велись дискусi¨,

наведемо

Парад к

iз котом Шредин ера. Парадокс, я ий запропо у

ÿêа няотвiр,дногопу

. Íà

шляху отона

¹

-

ëåíå

àëî, ùî ç iìîâiðíiñòþ

1/2

вiдбива¹скриньцiîòî ç iìî iðíiñ þ

в в Е. Ш един ер, поляга¹ ось

÷îìó.

риньки,

Ч. а ан, як вiдотонамо, у 1930 роцi отримав Нобелiвську премiюнапiвпосрiбза iдкристiнкия

öi ¹

що може бути вiдкритий

÷ ñ,

необхiд ий для пропу

8

69

явищадзеркоìбiнацiйного розсiювання свiтла.

1/2 пропуска¹ його. Якщо

ïðîõ äèòü

дзеркал ,

îòîâií

òîþ, . . . ),

бiдолашн

ãî

котла

ÿ. ßêù

приводить у дiю пристрiй (рушниця, ампу

крiзьсинильною кисло

ÿ, ùî

перебува¹

суперпозицiйному станi: пройшов

дзеркалоотона вiдбивспозбавля¹iд дзеркала . Вiдповiдно до цього крiзькiт

дзеркала, отоннiчог

не вiдбува¹житться. Вважа¹ть-

вiдбива¹тьстобто м мо живомертâîãî

êîòà:

перебув

якийв суперпозицiйному станi мiж живим та мертвим,

1

живийрмiнованим,êiò

де замiстьстан кота

i

= √

{|

+ мертвий кiт

i}

,

|

2

|

-

-

окремлюютьсПарадокСутьУчитивописнiйнепарадоксаситуацi¨зника¹стан¹ма¹станднамидепевногоота,самеБройлякотввеличастинка,залежитьполяга¹чи¹дужкимоментнедет.значУвiдкПарижiякåтомуннявза¹модi¨того,дзерквали(живомертвийщощознахвiдкрилиальноп¨¨пiсля.значаютьНаспрдитобтоотвiдбива¹тьспотраплянняонямивдi,çкiт)аким,акритаамплiтудупристро¹мскриньку,недетермi.Вихящоскриньвiдпринотонадить,.щобстстi

ноквпобащоципвнускринькунiсть..

ψ

|

. Ó

âñò

перегородк

àêîæ iç

áèâ

чими стiнками,авля¹тьсдiлить ¨¨ на двi рiвнi скриньдзерки, щ

залишàþскринькуПа ижi. У якiй зi скриньок знахдодиться

частинка,

âiä

я. Одну з них вiдправляють

другу

ïîâíiñò

не детер

iновано:

це не означа¹, що частинкЛьвова,десьально¹,

Парадокпростополяга¹невiдомо

òîму, що спериментрезуль

ек перимепевноготу у Львовi

íàì

äå. Öå

ùî íå iñíó¹

ìiñöÿ ïå-

ребування

бто немознача¹,сенсу

виявлен я

ж всеаки

âîíà

. У Львовiчастинки,авиться ек

частинки.

ìèòò¹âî

вплива¹

ситуацiю в Парижзапитувати,детермiнованiстьтобто

ÿ äî

дносно

äî òîãî, ÷è ¹

ßêùî

аналiзувати цю сПарижтуацiю(безвпозицi¨ класичн ¨ iзики,прот

стверджупоширю¹тьсповну недетермiнованiсть стану частинки.

öå

Ï ðèæi, ÷è ¨¨ ò íåìà¹).

де саме. Тобто ст

iн ормацiядесь знах диться, але

íàì

ìó¹ íàñ ïðî òå, ÷è

âîíà ó

Львовi, чиневiдомоема¹. Квантова механiкан

частинкè

детермiнований

вiдкриван я скриньки лише iн ор-

70

Парадокс Айншт йна По

ого зена. З метою

що квантова мех

à

да¹ неп вний опис iзичних систем, А. Айн

øò

Б. Подольський i Н. дольськзен 1935 року опублi увалидовести,аттю

â ÿêié

ëè

ацiю, подiбну до парадо са де Бройля.

Заув жимо,запропонувщо анiкрадокситуШредин

ç éîãî

îòîì áóâ

¹юайн,цю статтю. Отже, нехай ма¹мо двi

вiдстань ж

якимистинокдорiвню¹ сталiй величинi

x0,

åðà частинки,

реакцiстему

¨õíié ïîâ

-

íþ¹

. Величина

ий iмпульс дорвiд

дитьз частибула.iмпуСутьб

рiвпульсюентвеликоюняпарадзначення.однi¹¨Тпоакухоса)не

(ìà¹ìî

ïàðшихадоксамидруго¨лiммiжòåполяга¹ментальноперчастинки,прiзвищимидетермiнованiстьназиваютьможтому,англiйськiйа¹моторкаючишвидкiстьматищо,EPRвимiрюючитой-будьпароюñмовiьамий-якеiн¨¨(авт,ормацiябревiатуразначеяк

вiдстаньче

x0

íîê,ëüñóp

á¨хзначенiмпульсу,тинокшвидкiстюудемо

x0

ÿпальнеотримат.окоорреалiзацi¨Мисутт¹вуднi¹¨ширю¹тьсявимiрюючиiншдинатищевивчзчастинехценелопевнiнняраззазi--

величинддетдночасно,гу

тинки,

ально¨

ïавеличинивимiрювасвiтлаðiснуютьадокда¹айзенберча зм

обтодопершо¨невизна.орi¨),Такимжцьогоджують,iмпульцiвеличиничаченостейEPRвимiрчином,утинки,щовiдповiднихдруго¨-

ствер

åбiльшою,ртíàтого,атисьципомтово¨.Т

ороненоальнiстьбезпосервплива¹.Крiмповянаприкладкваоординати

якого вреш i-решт привело до ек

имент

òàê

çâàí ¨ êâàíòово¨ телеп ртацi¨.

Ÿ 5. Хвильова ункцiя вiльно¨ частинки

На основi

Бройля ми встановили, що хвильов ю

ми докладно вивчигiпотези

óì âè íîð

вання плоских хвильпараграт ¨хнi

. ляд будемо вести як для обмеженого об'¹му

ïðîñ-

ункцi¹ю вiльно¨ частинки ¹ плоск

хвиля. У цьому

властивостiтору, для необìеженого об'¹ìó

простору, у якому руха¹ться

частинкак.

Почнемо зозгдновимiрного випадку, коли

де хвильовий вектор

ψ(x, t) = Cei(kx−ωt),

k та частота ω пов'язанi з iмпульсом та енер71-