Добавил:

shenkman Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

Квантовая химия

Файл:

Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

.pdf

Скачиваний:

Добавлен:

26.04.2021

Размер:

4.52 Mб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 8520 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

такi ж мiркування, як i щойíо наведенi, дають
акого~ланцюжкаω менша: Eспiввiдношень:− ~ω. Повторюючи цей процес, приходимо
	1
	~ω ˆb+ˆb + 2 ψ1′ = (E − ~ω)ψ1′
Îòæå, ÿêùî	ψ1′ = ˆbψ.
квант	ψ âiäïîâiäàëà åíåð iÿ E, òî ψ1′ = ˆbψ åíåð iÿ

íà

äî

ψ → E,

ψ′

= ˆbψ

→

E′

= E

−

~ω,

ψ′

= ˆbψ′

= (ˆb)2ψ

→

E′

= E′

−

~ω = E

−

2~ω,

................................ .........................................

Як бачимо,ψ′

=оператор(ˆb) ψ

E′ = E

n~ω.

→

−

стану,

бiльшу¹ енер iюназва:+квант,дiючи на деяку стартову амплiтуду

квант

~ωовiда¹,ератороператор b зменшу¹ E на

Пiдберемо+

породження,

якраторункцiю~ω

йогом вазнищенняйде.так,Звiдсиназивають,пробквантiвос¨херяовнийвакуумiя,.якст¨й.оговiдОзначеннястануïтепер цюбулаосновногостнайменшою,артовустанухвильовутобопеабо,

ψ0, iксу¹м рiвнянням:

постулат,гамiльтонiанануужмiркувань:левiякийне.Можнаiсну¹,мистанiвприйма¹мозахвильмiркудеякоюз âенерiаватихвильовоюункцi¨безi¹ющедоведенняменшою,йтакихт. ункцi¹юВiзьмемостанiвнiжнапiдставiпростоiнiмальсереддоiне¹

значеннярiвнюютьту¨тивнихЦе

bψ0

= 0.

hHˆ i = ~ω Z

ψ:

ψ ˆb+ˆb + 1/2 ψ dq = ~ω Z ψ ˆb+ˆbψ dq + ~ω/2

192

= ~ω Z

(ˆb ψ )(ˆbψ) dq + ~ω/2 = ~ω Z

|ˆbψ|2 dq + ~ω/2.

Çâiäñèi¨

ма¹мо, що завжди hHi ≥ ~ω/2, а мiнiм льне значення енер

~ω/2 досяга¹ться для тако¨ нкцi¨ ψуваги, як задовольня¹ умову

рiв.Аянняце

беручиосновногодо стануозначення.

bψ = 0

Шрединнашеозначенняера,

ходимо енер iю основного стану

ψ0, çíà-

E0:

ˆ+ˆ

= E0ψ0,

~ω(b b + 1/2)ψ0

Cn ñòàëi

~ω

Îòæå,

Отже, розв'язок нашо¨ задачi òàêèé:

2 .

ψn = Cn(ˆb+)nψ0,

C0 = 1

äå

En = ~ω(n + 1/2).

нормування. Обчислимо ¨х.

або в явному виглядi

Z ψnψn dq = 1,

Äàëi

|Cn|2 Z

h(ˆb+)nψ0i (ˆb+)nψ0 dq = 1.

+ ψn

−

+ ψn

−

Перекиньмо дiю оператораˆ

|Cn|

Cn−1

Cn−1 dq = 1.

ний оператор

(ˆb+) направо, увiвши транспонова-

(ˆb+) = (ˆb+)+ = ˆb:

Îñêiëüêè

Cn−1

Z ψn−1ˆˆbb+ψn−1 dq = 1.

òî

ˆ+ˆ

~ω(b b + 1/2)ψn−1 = En−1ψn−1 = ~ω(n − 1 + 1/2)ψn−1,

ˆˆ+

ˆ+ˆ

= [1 + (n − 1)]ψn−1.

193

I. О. Вакарчукbb ψn−1 = (1 + b b)ψn−1

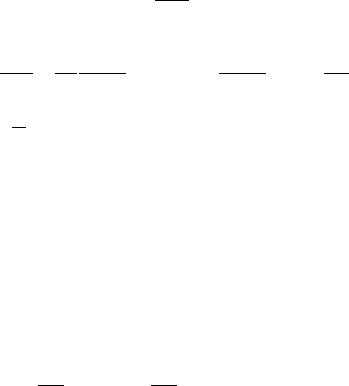
Тепер ма¹мо

Cn−1

n Z

ψn−1ψn−1 dq = 1,

−

n = 1

льабовiз точнiстюункцi¨, до

азового ìíîжника, з якою визначаються хви-

Ма¹мо рекурентну ормулу:

−

= √n .

Cn−1

1 Cn−2

Cn−3

Cn =

√

= · · · =

√

n − 1

n(n − 1)

n − 2

Îòæå,= √îñò

аточно.

ˆ+ n

)

ψn =

√

ψ0,

рiвконПiдêðå

слимо,ногозображення,щомиотрималина якомуцейреалiзурезуль¹тьсат,янеалпебрареходячиоператодо

~ω(n + 1/2).

Знайдемо+

çíè-

щенняb

bхвильову.тепер резульункцiюат дi¨ операторiв породження

ˆ+ n+1

(b )

ˆb+ψn

ˆb+(b+)nψ0 =

p(n + 1)!

√

ψ0

(n + 1)!

194

ψn+1

= √n + 1 ψn+1,

(ˆb+)n−1

ˆb(ˆb+)nψ0

p(n

ˆˆbb+

ˆbψn =

√

− 1)!

ψ0

(n − 1)!

1)!

як i при обчисленнi стало¨ˆˆнормування, ми використали те, що

−

= √n ψ

n−1

ˆ+ˆ

= nψn,

b ψn

знайшли важливi рiвняння:ˆˆ

Ìè

ψn = (n + 1)ψn.

ˆ+

ψn

√

= n + 1 ψn+1,

òîðiâ

b ψn = √n ψn−1.

iндекзменшу¹ом,цiправсзгiдностануйва¹,лйогоiмпульсузхвильово¨легкоциминаодиницюзнахтправ¨хнiходимоункцi¨.лами,степенiвматричнiнаоператор.диницю,Зозначелемпородженняåíа нятиоператор

çТакимнищеннябiльшу¹Маючикоординати

ˆ+ âèïëè

ùî

b ò

xˆ = r

(ˆb+ + ˆb),

2mω

Тепер:

pˆ = ir

m ω

(ˆb+ − ˆb).

xn′n = hn′|xˆ|ni

= r

hn′|ˆb+ + ˆb|ni

2mω

13*

√n + 1δn′,n+1 + √nδn′,n−1 ,

195

2mω

(x2)n′n

= n′

xˆ2 n

n′ ˆb+ˆb+ + ˆb+ˆb + ˆˆbb+ + ˆˆbb n

h |

| i

2mω h |

| i

hp(n + 1)(n + 2) δn′,n+2 + (2n + 1)δn′,n

2mω

+n(n − 1) δn′,n−2 ,

= hn′|xˆ3|ni =

3/2

(x3)n′n

hn′|ˆb+ˆb+ˆb+ + ˆb+ˆb+ˆb + ˆb+ˆˆbb

2mω

ˆ+ˆˆ+

ˆˆ+ˆ

ˆˆ+ˆ+

ˆˆˆ+

ˆˆˆ

+ bb

b + bb

+ bbb

+ bbb|ni

зглянемо координатíå

çàìiíîþ

3/2

(n + 1)(n + 2)(n + 3) δn′,n+3

2mω

√

+ 3(n + 1) n + 1 δn′,n 1 + 3n n δn′,n−1

n(n − 1)(n − 2)

δn′,n−3 .

для оператора

Аналогiчнооператоринаведензн х мо матричнi е

ементи

èìó¹ìî ç

àìèõ âèùå îðìóë

множник

pˆ: ¨õ îò

(~/2mω)1/2

−

ðÿäê âèìèm~ω/íîìå2,

дужкахзамi знакию¹мо на+ знакбiля доданкiв з парними по-

представлення,. оли

xˆ = x,

pˆ = −i~d/dx,

ξ −

äå

ˆb = √

ξ +

ˆb+

= √

dξ

Знайдемо яв ий вигляд ξ = x ,r

mω

вакуумного

стану

його означенíÿ:

ψ0 = ψ0(ξ), виходячи з

196

= 0,

bψ0

Очевидно, що

ξψ0

dψ0

= 0.

dξ

ξ2/2

де сталу нормування

отриму¹мо з умови

ψ0

= Ce−

∞

Z−∞ |ψ0|2dx = 1,

так що хвильова ункцiяC =

mω

1/4

π~

mω

1/4

ξ2

хвильова

ункцiя збудженого стану

Тепер, за означенням,ψ0(ξ) =

π~

e− .

ˆ+ n

mω

1/4

ξ −

àáî

(b ) ψ

ψn(ξ) =

√

e−ξ

π~

dξ

2nn!

mω

1/4

ξ2/2

Åðìiòà, ç ÿêèì

âæå

знайомi з попереднього

граде полiнома

ψn(ξ) = π~

ìè√2nn! e−

Hn(ξ),

ïàðà-

ξ2/2

ξ2

товуютьраткпадку,мМетояквипадкленняня,âè застосову,йоговипадокявищаолиоператорiврiзнихомназивають,частинки¹тьсянадплинногатистикиальногозадачахдопородженняабописуквантово¨предстñòiÁîçåелементарiелектромагнiтно.авленАйншт. Цетеорi¨знищенняiняайнапредстзбудженнявторинного.чисел.озгшироколянутезаповненняполмаютьàâëенн квантуван,пред¹викорисоливаньчасткцiлийдляав

ñïií

Hn(ξ) = e

ξ − dξ

e−

= e

−dξ

e− .

197

Торкнемось ще пит н я когерентних станiв. озгляньмо ор-

мально рiвняння на влàñíi значення для оператора знищення:

Ôó êöi¨

óíêöié

ψα утворю¹ повну сис ему.

÷åíiñòü

bψα = αψα,

b|α = α|αi,

αвий, iндекстомуйогопредствлàâëñíåннязначення(квантове число). Оператор b неермiто-

iìiçóþ÷èé

комплексне число. Набiрα = Re α + Im α

ψα

ñòàíами, якiназиваютьмiнiмiзуютьщеневизнакогерентними станамиайзенбер.а:Вони

¹ òèìè

ψα

е усередненняпорiвнятидбува¹тьсh( xрiвнянням) ihçà( ñòpанами) = 4

äконатись,лиранiше,якщо

рiвнянняз

íà

ìi

мiнiмiзуючихвласпакет,. Уе цьомуаченняяклегкмиоперрозгперелято

вленняðiâ ÿíêогерентнихÿ (ç òî÷íiñòþíiâäî

ìíîbжниквоординаа)¹ днаковиминомупредставленнi.Томупредст цi

ψiâα .Цiкавоще

називаютьнавестипредстрозклвiдношенняàвленням

хвильов хПростеопераê

ò ðà

ψα

залиша¹моядвла ми станами

ˆ+ˆ, тобто за х ильовими ункцiями

ñц лятора

ψn

b b

àê æ

îведення3цьогодляцьогоспiâ парагра а):

÷åâi (äèâ..

Приклад

α 2/2

∞

αn

осцилятораня ЕренПрикладеста,з1гамiльтонiаном.тобтоМатричнийрiвнянняψ = e−|

ψ .

пiдхiдрухудодляосциляоператтор

но¨орiвзадачiкоординати. Запишемотiмпульсурiвнян-

n=0

√n!

xˆ

/2:

H = pˆ /2m + mω

дженняв1981926

pˆ

Назвароцiкогерентнихвiдобража¹Е.Шрединджерелтойер. акñâiò,тлащо (1963.€лаубер.). Упершецiстаницiзастосуваванирозглянувдлядослiще-

x˙ =

p˙ =

−mω xˆ.

риставшисьПоставимодругим,ще познаходимооднiй крапцi злiва i справа в першому рiвняннi i, ско-

ˆ 2

Вiзьмемо матричний елемент, побуx¨ +дованийω xˆ = 0.на власних ункцiях оператора

Далi пригада¹мо, що з рiвняньx¨knайзенбер+ ω xkn =виплива¹0.

	x˙ kn = iωknxkn,
i тому наше рiвняння да¹x¨kn = ωknx˙ kn = −ωkn2 xkn,
Îòæå,	ω2 − ωkn2 xkn = 0.

матрицi xkn 6= 0 ëèøåX за умови, що ωkn = ±ω. П ренумеру¹мо елементи

xматричнийkn ак, щобелементнульовi значення познач лись сусiднiми iндексами: нальнийxn±1,n 6= 0, ωn±1,n = ±ω. Виразгамiльтонiана,дляенер i¨ знàéäåмо, обчисливши дiаго-

mω2

En = (H)nn =

(x˙ )nn

(ˆx)nn

m X

mω2 X

x˙ nk x˙ kn

xnk xkn

ωkn +

xnk xkn

дiагональних

m 2

2 ωn+1,nxn,n+1xn+1,n +

ωn−1,nxn,n−1xn−1,n

m 2

(xn,n+1xn+1,n + xn,n−1xn−1,n)

агада¹мо, що з умови= mωермiтовостix +îïx ратора, координати

n+1,n

n−1,n

матричнiйèõ ñïiââiäí øåíü

~ òà

xkn=xnk. З перестав-

ðìi äëÿ

ìà¹ìî

àáî â

xˆpˆ − pˆxˆ =

елементiв

xˆx˙

pˆ = mx˙

− x˙ xˆ = i /m,

(ˆxx˙ )nn − (x˙ xˆ)nn

(xnk x˙ kn − x˙ nk xkn) =

199

m 2 m 2

àáî

çíà÷åííÿì, x0,−1=0. Òîäi î÷å-

видно

n=0, òîìó, çà

xnk xknωkn =

xn2 +1,nωn+1,n + xn2 −1,nωn−1,n =

Ми отримали рекурентне рiвняння для

= 2mω .

xn+1,n − xn−1,n

An = xn,n2 −1:

Бу емо починати нумерацiюAçn+1 − An =

2mω

Çâiäñè çíàõ äèìî (ç

òî÷íiñòþ äîAnàçî=

множника)

âîãî n.

2mω r

решта

xn,n−1 = xn−1,n =

2mω

xn,k = 0. З виразу для енер i¨ знаходимо

тобто

En = mω2

(n + 1) +

n ,

2mω

льсненопредстрiвнiавленняенер~операториi¨ дляматричнiосциляторно¨елементизадачiоператорiв. У цьому.

представленнiЗадачаПрикладрозв'язана:2. Iмпузнайд

En =

ω(n + 1/2).

pˆ = p, xˆ = i~ d/dp,

√

b = i(η + d/dη)/

äå

ˆ+

= −i(η − d/dη)/

√

ω.

Для основного стану ма¹мо

η = p/

bψ0(η) = 0,

де з умови нормування

ψ0(η) = C0e−η2/2,

C0 = (π~mω)−1/4. Äàëi

ˆ+

(b )

−

остатАбо, îчнопускаючима¹мо:

àçîâèé

згадавши означенíÿ

ψn

(η) =

√n! ψ0

= √n!2n

(π~nω)1/4

(−i)

− dη

ìножниê i

ïîëiíîìiâ Åðìiòà,

200

ψn(η) =

√

e−η

/2Hn(η).

(π~mω)1/4

n!2

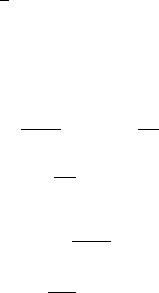
иклад 3. К	стани. Знайдемо розклад когерентних станiв			çà
хвильовими ункцiямигерентармонiчного		осцилятора i доведемо ¨хню повноту.
Ïðàöþ¹ìî â ïîзначеннях Дiрака, i отже,
	X∞		n′ = n − 1, ïîòiì
	ëiâiй частинi
	\|α =	Cn\|n ,

n=0

няння|ni перепознакет-власнiвекторизначеннягармонiчногооператîсциляторазнищення.Пiдставимо цей розклад у рiв-

i çíàõ äèìî

b|αi = α|αi

X∞

àáî,

чаючи iндекси√â

ортонормован вняння (

Cn n|n

− 1i

= α

Cn|ni,

n=0

рекурентне′

спiввiдношення:

ñòàíiâ , ′

), знах димо, зважаючи на

iñòü

|ni hn

′

n → n

|ni = δn n

Çâiäñè

Cn√n = αCn−1.

αn

òîìó

Cn = √

Cn−1

= √

√

Cn−2 = . . . =

√

C0,

n − 1

X∞ αn

а з умови нормування

|αi = C0

√

|ni,

n=0

hα|αi = 1 знаходимо сталу C0:

∞ X∞ α n′ αn

hn′|ni

hα|αi = |C0|2

√

n′!n!

n=0 n′=0

2 ∞

i з точнiстю до азового множника= C0

= C0

2e|α|

n=0

Остаточно

C0 = e−|α|2/2.

α 2/2

X∞

αn

Цей вираз можна записати через−оператор| |

ïîð

одження

|αi = e

n=0

√n! |ni.

ˆ+ ùå é òàê:

ˆ+

|0i.

|αi = e−|α|

/2+αb

201

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 8520 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Соседние файлы в предмете Квантовая химия

#
26.04.2021258.33 Кб3Correlation.pdf
#
26.04.2021200.52 Кб1MO_vs_VB_and_CI.pdf
#
26.04.20214.52 Mб10Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B.pdf
#
26.04.2021482.19 Кб2Valence_bonding.pdf
#
26.04.202166.54 Кб4формули.pdf