
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
визнача¹мо з рiвняння |
|
|
|
|
|
|
|
|
|
|
|
||
цi розв'язкиДругийрозв'язокнумеру¹моAi′( визнача¹εпарними) = 0, непарнучисламиn = 0 хвильову2,.4, . . . ; óíêöiþ |
|||||||||||||
|
|
− n |
|
|
|
|
|
|
|
||||
íàê + äëÿ |
ψn(x) = ±CAi(|ξ| − εn), |
|
|||||||||||
ç рiвняння |
x ≥ 0, çíàê − äëÿ x ≤ 0, а рiвнi енер i¨ знаходимо |
||||||||||||
цi розв'язкиЗумовинормуваннянумеру¹моAi(−εn) = 0, |
n =числами1, 3, 5, ... . ; |
|
|||||||||||
|
|
|
|
непарнимима¹мо |
|
|
|
|
|||||
àáî |
|C|2 |
Z∞ Ai2(|ξ| − εn) dx = 1, |
|
||||||||||
i ïiñëÿ çàìiíè 2|C|2 |
|
−∞ |
Z0 |
|
|
(ξ − εn) dξ = 1, |
|
||||||
2mα |
Ai2 |
|
|||||||||||
|
|
~2 |
|
|
1/3 ∞ |
|
|
|
|
|
|||
íèêà |
z = ξ −εn знаходимо з точнiстю до азового множ- |
||||||||||||
|
v |
|
|
|
|
|
|
|
|
||||
ункцi¨,Нарештiзалежно¨остаточнийC =âiä1 |
|
|
|
|
|
Ai (z) dz. |
хвильово¨ |
||||||
|
|
,u mα |
1/3 |
Z |
|
||||||||
|
|
|
|
u |
4~2 |
|
|
∞ |
|
||||
|
|
|
|
u |
|
|
− |
|
|
|
|||
|
|
|
|
çàãàëüíий вигляд2 нормовано¨ |
|
||||||||
|
|
|
|
t |
|
|
|
|
|
|
|
||
ξ, ¹ таким:
ψn(ξ) = (±)n " Ai(|ξ| − εn)#1/2 ,
R∞
2 Ai2(z) dz
|
−εn |
верхнiй знак + для |
Z∞ ψn2 (ξ) dξ = 1, |
|
−∞ |
222 |
ξ ≥ 0, à íèæíié − äëÿ ξ ≤ 0. |
|
|
|
|
|
44581 |
|
|
|
|
|
7297368321 |
|
|
|
|
|
809 |
|
|
|
09 |
726 |
|
6543210 |
4321.16330524087943301879208155 |
|
|||
65 |
εn |
|
|||
n |
|
|
|||
7 |
|
7867 |
7 |
|
|
8 |
7 |
372 |
|
359 |
|
9 |
944 |
|
|
||
10 |
8.48848 |
673 |
|||
СтигУаблицi подано першiзловуди адц ть рiвнiв енер i¨ ε тинкинуИСправочнизнайшли.Насамкiнецьрисбулаункцiйаняк. (безмежно21Мпонулi.под:несиметричнкiлькНаука,специальнымзаноуважимункцi¨охбевисок1979,çб джениЕйрiю,нащосторнкциунõявильстанiêöi¹þ.¨¨ÿ294)мопопотенцiальâ.у,хiдно¨По.якiункцiюредмають(див.Мювалаосновного..,вузлиАбрамовицаенернаприn,.iяяêiлад,часстми
|
α > 0, x ≥ 0 |
x |
äîðiâ |
U (x) = |
αxöi , |
абувала áезмежного начення |
â òî÷ |
||
x |
= 0 |
стiнка),тобторозв'яçокточцiако¨ |
çàäà i |
|
ψð(âíix) =åíåðCAi¨(ξ−εn) з умовою ψ(0) = 0 |
Ai(−εn) = 0. Причому |
|||
то их чисел εn збiгаються з нав деними вище для непарних кван буЦям'яч,хнi а¹тьсяЗемлi,задачащоруха¹тьсперiодичнодецимацiя¹nквантовим= 1, 3, 5,днорiдномупадаючи.станiв.аналогом.. Отжзнейтронiве,парнимизавдякикласвiдбиваючисьравiтацiйномучно¨хвильумовiшкiльно¨овимиполiiдне¨бiлязадачункцx( =п0iямивервiдпро.
α = g,
gконаноих станiвприскоренняунiкдляальнийувiльноготрахолоднихекспериментпадi ня)зi спостереження.Нещодавно(швидкостiâпершеакихбуквантоло ви-
ùîàêiäспотворенняпадаютьгоризонтальногожустановлпiдньþдi¹ютонiвськватинейтронногонижнюравiтацiйногоравiтацiйногомежудзеркалавiдстанi,поляЗемлi.потенцiалуЦейпiслядослiдвiдбиваютьсяко¨2(Hartmutдозволя¹можливiсм/сек),223
|
#q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
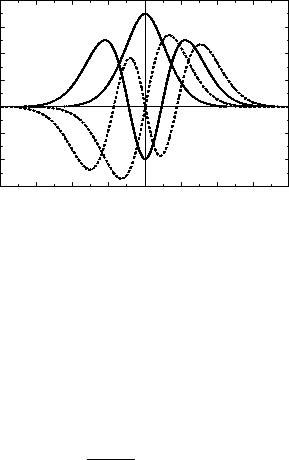
ис. 21. Хвильовi ункцi¨ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
ëüîâi óíêöi¨ ( |
|
| |-осцилятора. Суцiльнi лiнi¨ парнi хви- |
|||||||
( |
n = 0 2), пунктирнi лiнi¨ непарнi хвильовi ункцi¨ |
||||||||
Abele,n = 1 3Stefan). |
Bae |
|
|
|
|
|
|
|
|
v1.)Цiк.розкладамивотакжßðler,зглянутиAlexanderвласнiWestphal,значенняpreprintенерhepi¨ -ph/0301145 |
|||||||||
|
|
î |
числа |
|
|
|
|
εn |
äëÿ âåëè |
ðåêõ çíвиразчень квантвище |
|
|
|
|
|
|
|||
явниймиомендованого.Для |
цьункцi¨ |
|
|
|
(дивзаписсь.íàтисстормптотичдля.них267 |
||||
|
|
îãîдовiдника):намЕйрiпотрiбноn, коли¨¨похiдно¨скористатможна |
|
- |
|||||
Ai(−z) = |
1 |
|
|
|
2 |
z3/2 + |
π |
, |
z1/4√ |
|
sin |
|
|
||||
|
3 |
4 |
||||||
π |
Звiдси знаходимоAi′(−z)íóëi= − √π |
cos |
3 z |
|
+ 4 |
|
, z → ∞. |
||||||||
|
|
|
z1/4 |
|
2 |
3/2 |
|
π |
|
|
||||
|
|
|
|
|
óí |
êöi¨ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Ai(−ε), |
|
|
|
|||
|
2 |
3/2 |
+ |
π |
|
|
|
|
|
|
|
|||
224 |
|
εk |
|
|
|
= kπ, |
|
k = 1, 2, 3, . . . , |
||||||
3 |
4 |
|
|
|||||||||||
òà ïîõiäíî¨ Ai′(−ε),
|
|
|
|
2 |
3/2 |
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
|
|
k = 0, 1, 2, . . . . |
|
|
|
|
|
|
|
|
||||||||||
Öi äâi îðìóëèε îá'¹ä+ íó¹ìî= (2kîäíi¹þ+ 1) : , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
3 |
k |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
3π |
|
|
2/3 |
|
|
|
|
|
|
1 |
|
2/3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
n = 0, 1, 2, 3, . . . |
|
|
|
|
|
|
|
||||||||||||
|
|
εn = 4 |
níå+ï2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
причому перша óìîâà ä๠|
|
|
|
|
арнi значен я |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Мiж iншим, ця ормула да¹ |
|
осить добрi значенняn, а друга п р i. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εn i äëÿ |
|
|
|
|
||||
квантових чисел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наближì ëèõ |
||||||||||
не значення енерni¨.Зокрема äля основного стану n = 0, |
чення- |
|||||||||||||||||||||||||||||||||||||||
äîðiâíþ¹ |
|
|
|
|
|
ε0 = (3π/8)2/3 |
|
= 1.115460, |
точне зна |
|
|
|
|
|||||||||||||||||||||||||||
Прикладε0. Обчислити= 1.018793рiвнi. |
енер i¨ частинки маси |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
m â ïîëi |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
àëi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
U = mωамiльтонiанx /2 + α|можнаx|; −∞записати< x < ∞;òàê:ω , α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
ˆ |
|
|
pˆ |
|
|
mω |
2 |
|
|
|
|
|
|
α |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
α |
|
|
|
|
|
|
|
|
|
|
|||||||||
çíàê + äëÿ |
|
|
H = |
|
+ |
|
|
|
|
|
x ± |
|
|
− |
|
, |
|
|
óíêöié) |
|
|
|||||||||||||||||||
|
|
2m |
|
2 |
|
|
|
mω2 |
|
2mω2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(термiнологiю |
|
|
||||||||||
породжено¨ модулемx > 0, çíàê − äëÿ x < 0. Якщо б не було цi¹¨ змiни знака, |
||||||||||||||||||||||||||||||||||||||||
осцилятор зi змiщенимсутт¹во|xðîçâ'ÿçê| точкуU , òî ìè |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
гармонiчний |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мали б задачу про лiнiйний |
|
|
|
|
|
|
|
||||||||||||||||
величину |
|
2 |
|
|
2 |
|
|
|
|
(−α/mω ) п ложен ям рiвноваги |
зсунутими |
|||||||||||||||||||||||||||||
ез точку |
(−α /2mω ) |
внями енер i¨. З |
|
iíà ç |
|
àêó |
|
ˆ |
|
|
|
ехзнероздiче |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H ïðè ïå |
|||||||||||||||||||
iвняння Шрединx = 0 |
ера, позмiдiбною¹якситуацiю,для i ми повиннi |
|
íàõ ä òè ðî â'ÿçê |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
осциляторацилiндраера. з нашим гамiльтонi |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ðiâíÿ |
|
ня-Шредин |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
параболiчногоом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
аномОтже,¹добрезагальнимвiдомi ункцi¨ |
|
|
|
|
|
|
|
|
|x| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
z), äå |
|
|
|
|
||||||
ìiðåíà çìi |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−a−1/2 |
|
|
|
- |
|||||||||
óìîâ(äèâ. |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
. Ç |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
розрахункiвийнявизнахвильовихтекстi цьогоквазiточнупарагракцiй~ ¨хнiхадовiдник,параметрпохiднихвеличиназiспецiточцiльних |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
зшподава |
|
z = (x ± |
α/mω )/ |
|
|
|
/2mω |
|
|
|
|
|
|
|
|
a = |
−(E + α /2mω |
|
/~ω |
||||||||||||||||||||
|
|
|
|
|
потенцiалуðiâ iâ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 0потребуютьзнахдимо |
|||||||||||||||||
пiдберемовнянядля |
|
чення |
|
|
|
|
å |
|
|
|
i¨ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ихпараметриднак,знайти(ми ¨х |
|
|
|
не наводимо)розв'язкиE, ÿêi,.âçàã ëi êàæó÷è, äèâ. |
|
|
|
|
|||||||||||||||||||||||||||||||
чисельМоíæíà, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ÿ18): |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2, α òàê, ùîá |
|
|
|
|
|
a = −(n + 1/2), n = |
|||||||||||||||||||
0Åðìiòà, 1, 2, . . . |
тобто оли ункцi¨ параболiчного цилiндра зводяться до полiномiв |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
n/2 |
e− |
ξ2 /2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Hn(ξ) |
, |
|
|
, |
|
|
|
|
|
|
|
|
|
Hn(ξ) |
, åíåð iÿ |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
ξ = z/ 2 Dn(z) = 2− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
похiдно¨Параметривточцiпотенцiалу знаходимо~ |
|
|
|
|
1 |
|
|
|
|
α2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
óìîâ |
|
иваннÿ |
|
|
|
|
|
|
|
òà ¨¨ |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
En |
= |
ω |
çn + |
2 |
|
çø− |
2mω2 |
|
. хвильово¨ ункцi¨ |
|
|
|
|||||||||||||||||||
|
|
|
|
x = 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
15 I. О. Вакарчук |
|
|
|
|
CHn(ξ0) = C′Hn(−ξ0), |
|
|
|
|
|
|
|
|
|
|
225 |
||||||||||||||||||||||||
ðiв яння не ма¹ розв'язку, друге(äèâä๠|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 0, òî ïåðøå |
||||||||||||||
òóò |
C [−ξ0Hn(ξ0) + 2nHn−1 (ξ0)] = C′ [ξ0Hn(−ξ0) + 2nHn−1(−ξ0)] , |
||||||||||||||||||||||||||||
C, C′ |
сталi нормування, |
ξ0 = α/ |
√ |
~ |
mω |
3 |
|
i ми враху али, що похiдна |
|||||||||||||||||||||
dH Беремо(ξ)/dξ =äî2nHуваги,(ξùî). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
n−1 |
Hn(−ξ) = |
−) |
n |
Hn(ξ) |
|
|
з нашихпотрiб |
|
|
|
||||||||||||||
ùî àáî |
|
|
|
|
|
|
|
i |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
âíÿíü çíàõ äèìî, |
||||||||
армонiчногоозв'язок,H (ξ |
енер) = 0 iя перший розв'язок, або ξ |
H |
n |
(ξ |
) = 2nH |
n−1 |
(ξ |
) другий |
|||||||||||||||||||||
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|||||
явнi вирази для полiнEnìiâ=Åðìiòìà¹ìî~ω(n + 1/2. −Ÿ21)ξ02./Зокрема,2). Теперякщо |
|
|
|
ìàòè ëè |
|||||||||||||||||||||||||
Очевидно, |
|
|
n = 3, |
E/ ω = (19 ± |
|
|
57)/8, |
|
|
|
7/2, 11/4; |
|
|
|
|
|
|||||||||||||
ã |
|
|
|
осцилятора |
|
|
|
|
|
|
|
ξ0 |
|
= 0 з енер i¹ю основного стану |
|||||||||||||||
à åíåð iÿ äîðiâíþ¹ |
~ω/2. Ïðè n = 1 перший |
îçâ'ÿçîê ä๠ξ0 = 0, |
|||||||||||||||||||||||||||
|
|
|
|
|
3~ω/2; а з другого ма¹мо ξ0 = ±1, енер iя ~ω. Ïðè |
||||||||||||||||||||||||
n = 2 |
з першого |
|
ξ0 |
= |
|
|
|
|
|
|
√ |
|
|
i åíåð iþ ~ |
|
, |
|
з другого |
|||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
±1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ξпродовжити0 = 0 ± 5/öþ2 процедурувiдповiднiдлявласнiбiльшихзначеннязначеньенерчислаi¨ 5~ω/2, |
|
5~ω/4. Неважк |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n: |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
ютьпотенцiально¨ницяŸУ25лишемiжкласичнiй. Прохдеякущо¨¨nцiенерповною=власнiсукупдж4,ìi¨.åE/нняхзначенняанiцiiстьенер~ω частинкирiвнiв= ðóõ(15i¹юенердля±частинки6)i¨конкретнихне/êðiçü4,вичерпують9/2¹,потенцiальнийнеможливим,(11зв'язкiвусього± 22)ìiæ/¨¨4.спектра,параметрамиякщобар'¹ррiзда-
åëðíiñòü÷èíою,перебуваннядодатна,це ознаствiд'¹мноючастинкил¹,бщод'¹мноюEкiнетичнарозв'язкуобластi,потенцiальною.Уквантовiйенердеiя, заUмеханiцiозначенням,¹вiд'¹мноюймо
цiальноюзвеличинаосцилятора:да¹,âi ерченнуалеозглянемоiячастинки.вiдмiннаЦе(аенердовидно,хвильовамеi¹юрухвiдсередн¹.зокрема,частинкинуляункц.знаЦе,чення.дляззрозумiло,Легкцiйзображдновимiрного¹областiвимiрюваноюпереконнезадачiознача¹,експоненцiальноEòèñü,−длявипадкуUвеличиною)<ùîгармонiчного0,кiнетич¨¨вiдмiнзсередпотенспа¹-
|
ßêùî |
,Uяк= Uрух(x)а¹тьс,ченняякзлiва направо,енарисма¹.22. нер iю |
|
ìå |
шу вiд максимàëüí ãî çíà |
E, |
|
ïèêó |
вонаитьсянев зможеточцi подîлати цього потенцiальнU (x), то у класичномубар'¹а,випадзу- |
||
226 |
x1, îëè E = U (x1), ïiñëÿ ÷îãî áóäå |
ухатись |
|
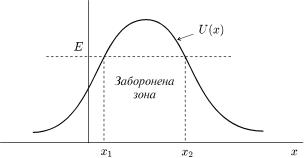
у протилежному напрямку тобто вiдiб'¹ться |
áàð'¹ðà. Ê îð- |
||
äèí òó |
x1 |
âiäìiííîþ |
|
точкмех |
|
|
|
|
поворотуназжлèâаютьимперебування¹рухкласичноюiзаб точкоюроненiйпотенцiальнийзонiворотуiж. Укласичквантîèìèâ |
||
àìèíiöiéìîâiðíiñòü |
|
|
|
ноенершийпроходженнявiдмiннатже, |
x1 ≤ x ≤ x2 |
|
|
|
|
|
- |
|
|
|
ié |
|
|
|
îöëÿ,íiñòiä |
|
|
îвумоюзменшу¹ться,крiзьцiкаванаункцiювеличиною,такийвлас,томучастинкирозрахункузада.iзнащоднаквоначенняхвильова¹цiйнамтзабороненiйзадвлункцiяснiймовiрнна,р'¹рвiднеобх.ункцi¨:Ценуз |
|
бластi,знайтитипiячастинкихочавiдзадач,лишенулячастинкизначнонiжхвиль.¹Виника¹вiдзадача |
|
||
|
èñ. 22. |
|
üíèé áàð'¹ð. |
|
|||
Припустимо, зл |
на бар'¹рПотенцi лiт |
¹ ч стинка iз заданою гус |
|||||
|
вiдбиваннярностi |
|
. Нехай чàстина |
|
|
||
тиною потоку ймов |
|
j0 |
|
|
j1 |
|
|
ó¹ ðóõ ïiñëÿ |
|
|
|
|
|
||
|
|
|
частинки вiд б р'¹ра,цьогоа потоку пи |
||||
ñправа вiд бар'¹ра, тобто в областi |
|
|
j2 öå ïîòiê |
||||
коном збереження потоку, |
|
x > x2. Очевидно, згiдно з за- |
|||||
|
|
|
вимiрюванi |
|
|
||
Уведемо експериментальноj0 = j1 + j2 |
. величини: вiдношення |
||||||
|
|
бар'¹ра,iцi¹нтомапроходженнявеличину |
êðiçü áàð'¹ð àáî |
||||
ÿêîå будемоiцi¹нтомназиватипрозоростiкое |
D = j2/j0, |
|
|
||||
15* |
|
|
R = j1/j0 |
|
|
227 |
|
кое iцi¹нт вiдбивання вiд бар'¹ра. Очевидно, що
тьсяНагада¹мозазагальнимтакож,виразомщогустинаD + R потоку= 1. |
ймовiрностi розрахову¹- |
||||||
поворотульово¨ ункцi¨ т |
x1 ≤ x ≤ x2 |
|
òîêó) |
|
|||
|
розрахункуj =â |
mi ψ (x) |
dx |
− |
ψ(x |
dx |
. |
|
x1 x23), |
dψ(x) |
|
|
dψ (x) |
|
|
|
|
~ |
|
|
|
||
Äëÿ |
|
åëè÷èíè |
|
|
|
|
|
кцiю частинкизлiва вiд бар'¹раDпотенцiальнаR необхiд о знайти хвиль ву ун
всерединi бар'¹ра |
|
x < x1, справа вiд нього x > x2 àõò |
|||
|
|
|
|
|
- |
|
|
урахуванням(п в кперервносасичнихямокутнийî÷êi õâè |
|||
¨¨ першо¨ |
хiдно¨вiзьмемо |
|
|
|
|
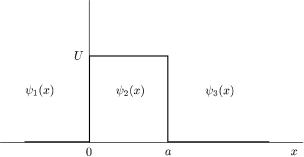
бар'¹рСпростимо(див. риснашу. . колизадачу |
|
енерякмоiядель пр |
|||
|
0, |
x < 0, |
≤ |
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U (x) = U = const, 0 x |
|
a, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
x > a. |
|
||
|
|
||||
ис. 23. Елементарний прямокутний бар'¹р.
ма¹моУпершiйрiвнянняобластiШрединx <åðà0 äëÿ |
хвильово¨ ункцi¨ ψ1 = ψ1(x) |
||||
228 |
− |
~2 d2ψ1 |
= Eψ1, |
||
|
|
|
|||
2m dx2 |
|||||

Кое iцi¹нти прозоростi та вiдбивання
|
D = íA1 |
|
, |
R = A1 |
|
. |
|||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
C1 |
|
|
A2 |
|
|||
шо¨Ураху¹мопохiдно¨тепервточкахумови |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 0 |
à x = a: |
|
|
|
||||
|
|
|
|
ψ1(0) = ψ2(0), |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ1′ (0) = ψ2′ (0), |
|
|
|
|||
|
|
|
|
ψ2(a) = ψ3(a), |
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
êîå |
|
|
ψ2′ (a) = ψ3′ (a). |
|
|
|
||
рiвнянняВикористовудля |
явнийiцi¹нтiввигляд |
хвильових |
ункцiй, знаходимо |
||||||
äà¹òüñ ïàäàþчим потоком A2, B1, B2 |
òà C1 |
(êîå iöi¹íò A1 çà- |
|||||||||||||||
|
|
|
|
|
|
j0): |
|
|
|
|
|
|
|
|
|
||
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|||
|
A1 + A2 |
= B1 + B2, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2) = k(B1 |
|
|
B2), |
|
|
|
|
|
|||||
k0(A1 |
|
|
|
|
|
|
|
|
|||||||||
|
ika |
|
|
|
|
ika |
|
|
|
ik0a |
, |
|
|
|
|
||
|
B1e + B2e− |
|
= C1e |
|
|
|
|
||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ika |
|
|
|
ika |
|
|
|
|
ik0a |
|
|
|
|
k B1e |
|
|
|
B2e− |
|
= k0C1e |
. |
|
|
||||||||
озг янемо спочатку випадок |
|
|
|
|
|
|
|
|
|
|
|||||||
Ïîäiëимо всi рiвняння на |
|
|
E > U , коли величина k ¹ дiйсною. |
||||||||||||||
|
|
|
|
|
|
A1, позначаючи |
|
|
|
|
|
||||||
Òàê ùAî2 = A, |
|
B1 |
= B, |
|
|
B2 |
= B′, |
|
|
C1 |
= C. |
||||||
|
A1 |
|
|
|
|
|
|||||||||||
A1 |
|
|
|
|
|
|
|
A1 |
|
|
|
|
A1 |
||||
230 |
D = |C|2, |
|
|
R = |A|2. |
|
|
|
|
|||||||||
Тепер система рiвнянь набира¹ вигляду
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
ñистеми, |
|
|
|
|
|
|||||
|
|
k0 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 + A = B + B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
(1 |
− |
A) = B |
− |
B′ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жившиДодамо |
|
|
|
|
|
|
Be |
|
|
|
B′e− |
|
|
|
|
|
|
|
= Ce . |
|
|||||||||||||
|
|
|
|
|
|
ika |
|
|
|
|
|
ika |
|
|
|
|
|
|
|
|
ik0a |
, |
|
|
|
|
|
|
|||||
|
|
|
|
Be + B′e− |
|
|
= Ce |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ka |
|
|
|
|
|
ika |
|
|
|
ik0a |
|
|
|
|
|||||||||
|
останн¹трет¹iчетнаâåрте рiвняння цi¹¨ |
|
|
|
|
|
|
|
попередньо помно- |
||||||||||||||||||||||||
|
|
|
|
|
|
k0/k, |
|
|
|
|
|
1 + |
|
|
k0 |
eik0a |
|
|
|
|
|
||||||||||||
та вiзьмемо ¨хню |
|
|
2Beika |
= C |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
рiзницю |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|||||||||||
Отже, отрима¹мо 2B′e−ika = C 1 − k0 |
eik0a. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
1 + |
|
k |
eik0a, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
B = |
|
|
e−ika |
|
|
0 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
2 |
|
k |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
B′ = |
2 e |
|
|
1 − k e |
|
. |
|
|
|
|
|
||||||||||||||||
Пiдставимодругецiнавиразиживши |
|
|
C |
|
ika |
|
|
|
|
|
k0 |
ik0a |
, попередньо помно- |
||||||||||||||||||||
ó äâа перших ðiвнянн |
|||||||||||||||||||||||||||||||||
|
|
|
k/k0, знайдемо рiвняння длÿ вiдносних амплiтуд |
||||||||||||||||||||||||||||||
A à C: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ eika 1 − k , |
|
||||||||||||
|
1 + A = 2 eik0a e−ika 1 + |
k |
|
|
|||||||||||||||||||||||||||||
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
k0 |
|
|
|
|
|
|
|
|
k0 |
|
|
|||||
1 − A = 2 eik0a k0 |
e−ika |
|
1 + |
|
k − eika |
1 − k |
. 231 |
||||||||||||||||||||||||||
|
|
C |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
k0 |
|
|
|
|
|
k0 |
|
|||||||
