Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

X

як сво¹ю чергоюψ (q) =¹ власноюC ϕ óíêöi¹þ(q)

оператораα = 1, . . . ,

s,

nβ

рiвнянь,

αβ

nα

α

âëàсному значенню

ˆ

A, ùî âiäïîâiäà¹

óíêöi¨

An. Êîå iöi¹íòè Cαβ пiдберемо так, щоб новi

ψnβ (q) були ортонормованими:

умова

Z

ψnβ

′(q)ψnβ (q)dq = δβ′,β

öÿ

з да¹ систему

з як ¨ визнача¹мовипадкуое iцi¹нти

Cαβ

åîä-

Процедура. . Справдi,ортогоналiзацi¨замiстьнаборудлявироункцiйдженого

нозначною

X

ψnβ , вiзьмемо iнший

ψnγ′

Äàëi

=

aγβ ψnβ .

β

перетворення)

X

Z ψnγ′ ′(q)ψnγ′ (q)dq =

X X

Z ψnβ′(q ψnβ (q)dq

β′ β

aγ′β′aγβ

Якщо пiдiбрати кое iцi¹нти= òàê,a

ùîáa

(унiтарне.

γ′β

γβ

β

X

òî íîâi óíêöi¨

aγ′β aγβ = δγ′,γ ,

β

цi¨нальностiвизначаюТаким.чином,Оψnγ′

(q)

òьсяже,ортогональностiзуякщоточвипадiстюакпiдужiндексомвиродженогодобудутьунiтарногозадовольнятиспекперетвореннярахвильовiумову.ортогоунк-

(

n розумiти складний iндекс

n, α), то умову

Z

пишемо

виглядi

ψn(q)ψm(q)dq = δn,m.

123

δ- óíêöi¨:

ченнящоумирухзамкненостi:системут3

ðаторiвосторуункцiй( аб р).утворювiльно¨унк

цiйютьчастинки,цюОзнаТвердженнязамкнеумову

кож¹тьсяВласнiужвункцiйнеобмежнехаймалиункцi¨. мидляеномуермiтовихма¹мохвильовихоб'¹мiсистемуопе

à.Z ψA(q)ψA′

(q)dq = δ(A − A′)

-

ψn(q)

мкненою,

{ψn(q)}

спробуймо представити ¨¨

виглядi.Вiзьмiмо

äîâiëüíó

óíêöiþ

ψ(q)

i

ψ1

(q), ψ2

(q) . . . , ψN (q)

N ′

X

äå

ψ(q) =

Cnψn(q) + RN ′(q),

n=1

назива¹тьсявлзàснi ункцi¨якщоермiтового оператора. Система

ïðè÷îзгмуляньмоN жщебутиiншуяк скiнченнимормузаписучислом,умови замкненостiакбезмежним.

N ′

2

X

2

Nlim′ N

|RN ′(q)| dq =

Nlim′ N

ψ(q)

−

Cnψn(q)

dq = 0,

або, iншими словами, коли викону¹ться рiвнiсть

Z

Z

→

→

n=1

N

X

ψ(q) =

Cnψn(q)

n=1

N

X

Z |RN (q)|2dq = Z |ψ(q)|2dq − n=1 Cn Z ψ (q)ψn(q)dq

N

N

N

X

X X

124

− n=1 Cn Z

ψn(q)ψ(q)dq + n=1 m=1 CnCm Z

ψn(q)ψm(q)dq.

Будемо вимагати, щоб

а це означа¹, що

Z

|RN (q)|2dq = min,

çâiäêè

δCn Z |RN (q)|2dq = 0,

δ

êîå iöi¹íòè, − Z

ψ (q)ψn(q)dq + Cn = 0,

тобто

що реалiзують мiнiмум величини

R |RN |2dq:

Cn = Z

ψn(q)ψ(q)dq.

Таким чином, при так пiдiбраних кое iцi¹нтах

N

2

X

2

2

Отже, умову замкненостi запишемо так (рiвнiсть Парсеваля):

Z

|RN (q)|

dq = Z

|ψ(q)| dq − n=1

|Cn| .

Систему ункцiй

Z

|ψ(q)|2dq = n=1 |Cn|2.

N

X

сукуютьНазва

моюнасисункцiйема,що .задовольняютьункцiйповсiхдитьцювiдумовутого,називащодо-

ïностiовноюзамкнсистå {ψn(q)}

óíêöiþ, ÿê

áóëà á îð

гональноювже не можна пiд'¹днати ще

íó

{. . . ψn(q) . . .}

ëèøå, îëè âñi

ψn(q). Це можлив

âñiõ

Cn = 0,

тобто пiд'¹днана ункцiя

доведенëÿ

ψ(q) = 0

ня. МиВоноq. приймемооза сщîрмудовiльнуоване ункцiювищетвердження 3 без

-

ð ä çà âëàñíèìè÷à¹, ункцiями ермiтового оператора:ψ(q) можна розкласти в

ψ(q) =

Cnψn(q),

125

n

X

де кое iцi¹нти розкладу

Якщо значок

Cn = Z

ψn(q)ψ(q)dq.

р'¹,внiтактобтозначення,йякiiнте¹розкладнiчимрувтонiншим,пiдуя.рядсумоюТакийзаяквласхвизароз

Ô ëüñó,

iìïó

кладс iдìèТвердженнярозумiтидеункцiямивжеБройлямали:якприйма¹.4пiдсумовування,.оператораВласнацебувйнепереядункцiя

n

ëÿíè

n

-

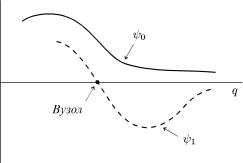
нижчомуднихвласномузначенняхзначеннюкоординатиоператора, не перетворю¹тьсяяка вiдповiда¹нуайль

ïðè

ψ0

= ψ0(q)

âóçëiâ).

q (кажуть, ùî óíêöiÿ íå ìà¹

ис. 16. Хвильовi ункцi¨ основного

ψ0

та першого збудженого

ψ1

станiв1 Зауваження:.

2◦

льово¨Це твердження,ункцi¨ однi¹¨загаломчастинкиажучи,. правильне лише для хви-

◦.

границiЯкщо рух вiдбува¹ться в обмеженiй областi простору, то на

3

èíi

областi.

. Îòæå,

мова йде про нулi ункцi¨ всере-

ψ0(q) = 0

◦

äîдатною,ψ0 не змiню¹ знака, ¨¨ можна вибрати дiйсною й

.

Ò ìó ùî

126

ψ0 = ψ0 ≥ 0.

маютьНехайспiльну систему власнихˆ ò ˆ ункцiйомутують.Доведемомiжсобою,це. то вони

A

B

ˆ

AψA = AψA,

озклада¹мо ункцiю

ˆ

BϕB = BϕB .

ψA â ðÿä çà ϕB ,

X

i ïîäi¹ìî

íà

íå¨

оператором

C(B)ϕB ,

ψA =

B

Îòæå,

ˆ

ˆ

Af (B), äå f äîâiëüíà óíêöiÿ.

ˆ ˆ

ˆ

X

ˆ

X

ˆ

З iншогоAf (áîêó,B)ψA = A

C(B)f (B)ϕB = A C(B)f (B)ϕB .

B

B

X

X

Однакˆ ˆ цi два виразиˆ

ðiâíi

ˆоскiльки оператори

f (B)AψA = f (B)AψA

= A мiжCсобою,(B)f (B)ϕB = A

C(B)f (B)ϕB .

B

B

омутують мiж собою

з цього виплива¹, що

ˆ òà

ˆ

A

B

Îòæå,

ˆ ˆ

ˆ

ˆ

X

Af (B) − f (B)A = 0.

X

àáî

ˆ

C(B)f (B)ϕB

A C(B)f (B)ϕB = A

B

B

X

ˆ

− AϕB ] = 0.

Унаслiдок довiльностif (B)óíêöi¨C(B)[AϕB

B

f (B) знаходимо, що

128

ˆ

AϕB = AϕB ,

Отже,довести¹якщоакож. двавласноюоператориункцi¹ю оператора

A

, ùî é ïîòðiáíî

булотобто ϕB

öèõí óíêöié

ˆ ˆ

A, B мають спiльну систему влас

iäíi içè÷íiψA,B (q),

маютьстанах,то нiщознаописуютьчення цi ункцi¨, вi

¹мо велич ну

держу¹м

çíà

A, B. Тобто, якщо

÷èíè,

,

цьому ж станi

â ìiðþвання

A

A

äíî-

èчинмiрюнекомутують?катè значеннямiжда¹Тодсобоюзнаiзичнихчення. величин,. Тому миякщможемооператори

часноАвелякщо

B

B

àëå

ˆ

AψA(q) = AψA(q),

причому

ˆ

BψA(q) = ϕ(q),

Ìè

можемо говорити, у якомулише проiзичнасередн¹ зна

A

ма¹цьзначенняому станi: .

ψA(q)

A

ПерейдемоНехайвеличин,заданодооператористанних hB

якихарактеристикине омутуютьˆ невизначеностей.

içè÷-

= Z

ψA(q)BψA(q)dq.

êiëüêiñíî¨

ψ(q), нехай далi

омутатор

де очевидно

ˆ ˆ

ˆ ˆ

ˆ

AB − BA = iC,

ˆ

вiдхилень:

оператори C ермiтовий оператор. Нагадаймо, що, за умовою,

ˆ òà

ˆ

A

B ¹ ермiтовими. Уведемо середнi:

hAˆi = Z

ψ (q)Aψˆ (q)dq,

Визначимо операториhBˆ = Z

ψ (q)Bψˆ (q)dq.

d

ˆ

− h i

d

ˆ

− h

ˆ

i

9 I. О. Вакарчук

A = A

A ,

B = B

B .

129

I(α) = Z

( A − αi B)ψ(q)

2 dq ≥ 0,

α

Âèêäiéñí

d

ˆ ˆ

d

ористовуючий параметрермiтовiсть. операторiв

Z

h d

d

A, B, ìà¹ìî

I(α) =

i d

d

( A + iα B )ψ (q) ( A − iα B)ψ(q)dq

Z

ψ

2

d2

d2

d

d

=

(q)( A + iα B)( A

− iα B)ψ(q)dq

d d d d

ìiíiìóì óíêöi¨

I(α) = (d

i

d

d d d d

=

h( A)

+ α h( B)

i

+ iαh

B A

− A B ,

h

d

2

i

2

h d

i

h

ˆ

i

Ми скористались тутA) òèì,+ α ùî(

B)

+ α C .

Знайдемо аке значенняA B − B

ˆ ˆ

ˆ ˆ

ˆ

A = AB

− BA = C.

α, яке приносить

I(α):

за умови

I(α) = min

ÿêà äà¹

dI(α)

= 0,

dα

Тепер ма¹мо

α = d

ˆ

B)2 .

2

ˆ

2αh( B)

i + hCi = 0,

−

1

hCi/h( d i

d

2

min

h

i −

4 hCi /h( d

i ≥

2

1

ˆ

2

2

Отже, остаточноI

=

(

A)

B)

0.

ˆ

2

130

(

A)2

(

B)2

i ≥

hCi

.

h

d

ih

d

4

Ми отримали узагальнене

нев значеностей. З

нього, як

овий випадок, випливають спiввiдноше ня айзен-

бер а длячасткоординати й iмпульсу,спiввiдношякi ми åннядержали рàíiøå :

ˆ

ˆ

ˆ

A = x,ˆ

B = p,ˆ

C = ~,

2

2

~2

iмпульсу:шихТепероператорiв,можна такожнаприклад,записатиx) äëÿ( pïî)компонентспiввiдношення. оператора моментуiдляiн-

h( c

ih

c äiáíi≥

4

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

Тому остаточноA = Lx

B = Ly

C = ~Lz .

~2

2

[ 2

2

DLˆz E .

Звiдси робимо

h( Lx)

ihùî( Ly ) i ≥

4

ê ñòi ðóõó íå

ають певног

çx аченнятаЯкщоумпонтанi,нтиу якомумоменту

êiëü

d

y

усереднення йде за -власом-

îнентаункцiянабува¹ì певногооператзначенраíÿ.

нимип

висновок,

, òî,

Lz

äå

ˆ

ÿê ìè çíà¹ìî,

ˆ

= ~m,

Lz

hLz

m = 0, ±1,

±2,

. . . i

òæå,

~4

Ïðè

h( Lx)2ih(

Ly)2

≥

m2.

4

m = 0 ìà¹ìî

тривiальну нерiвнiсть

d

d

2

2

≥ 0.

операт ра

скiль омпонентивсiвиняткомпонентиh( Lx)

ih( Ly)

для двох пар операторiвˆ ¹

òî öÿ

рiвнi ть викону¹ ься щеd

d

L

ˆ

ˆ

ˆ

ˆ

ночасно,че

îëè

êiëüê ñòi âñiðóõóiзичнихвожлиможнамаютьличинвимiрятинульовiткласузнаод.

Îтже,Одночасне.ê çà

точнемомвимiрюваннянтупадомутують,

Lx, Lz

Ly, Lz

рiвноправними,

ò

ê

åìî

A

в ннявеличоператоричин яких

âå. Òî÷ å âèìiðþ

B

íèõ

B. Однак вимiр рiз

èõ içè÷-

9*

A B íà ðiçíèõ åê

альних уст

овках да¹131