
- •Сборник лекций по курсу общей оптики
- •§ Фотометрические понятия и величины
- •§ Эволюция оптических теорий
- •§ Шкала электромагнитных волн
- •§ Особенности видимого диапазона
- •§ Электромагнитные волны (волновое уравнение)
- •§ Плоские волны
- •§ Сферические волны
- •§ Плоские гармонические волны. Волновой вектор
- •§ Представление гармонических волн в комплексном виде
- •§ Свойства элементарных и гармонических волн
- •§ Эффект Доплера
- •§Плотность потока энергии электромагнитной волны. Гауссов пучок.
- •§Импульсы электромагнитной волны
- •§ Давление света
- •§ Суперпозиция световых волн
- •§ Поляризация электромагнитных волн
- •§ Преломление и отражение на границе двух плоских диэлектриков
- •I. Законы геометрической оптики
- •III. Формулы Френеля
- •§ Полное внутреннее отражение
- •§Энергетические соотношения падающих, отражённых, преломленных волн
- •§ Элементы геометрической оптики
- •§ Виды оптических систем
- •§ Аберрации оптических систем
- •§ Условия наблюдения интерференции
- •§ Осуществление когерентных источников в оптике
- •§ Таутохронизм оптических систем
- •§Расчёт интерференционной картины от 2 когерентных источников
- •§ Многолучевая интерференция
- •§ Интерференция в параллельных лучах на клине
- •§ Эталон Фабри-Перо
- •§ Просветление оптики
- •§ Принцип Гюйгенса-Френеля. Метод зон Френеля
- •0 (В силу малости)
- •§Дифракция Френеля на круглом отверстии и экране. Зонная пластинка
- •§ Графическое вычисление амплитуды
- •§ Дифракция на крае полуплоскости
- •§ Дифракция в параллельных лучах
- •§ Распределение интенсивности в фокальной плоскости линзы при дифракции на одной щели
- •§Геометрическое вычисление интенсивности в фокальной плоскости
- •§ Дифракционная решётка
- •§ Наклонное падение лучей на решётку
- •§ Дифракция на многомерных структурах
- •§ Физические основы голографии
- •§ Двойное лучепреломление
- •§ Объяснение двойного лучепреломления на основании анизотропии диэлектрических свойств кристалла
- •§ Построение Гюйгенса в одноосных кристаллах
- •§ Получение поляризованного света. Поляризационные приборы
- •§ Получение и исследование эллиптически поляризованного света
- •§ Интерференция поляризованных лучей (хром. Поляризация)
- •§ Искусственная анизотропия
- •§ Вращение плоскости поляризации
- •§ Рэлеевское рассеяние
- •§ Комбинационное рассеяние света
- •§ Нормальная и аномальная дисперсия
- •§ Основы электронной теории дисперсии
- •§ Поглощение света. Закон Бугера-Ламберта-Бера
- •§ Фазовая и групповая скорости
- •§ Лучеиспускательная и поглощательная способность тела. Закон Кирхгофа.
- •§ Закон Стефана-Больцмана.Закон Вина. Формула Рэлея-Джинса
- •§ Формула Планка
- •§ Фотоэффект
- •§ Элементарная квантовая теория излучения (спонтанное и вынужденное излучение)
- •§ Инверсная населённость
- •§ Условия, необходимые для создания лазера
§ Суперпозиция световых волн
Принцип
суперпозиции: вектора
 в каждой точке равны
в каждой точке равны
 всех
полей в данной точке не зависимо от их
происхождения.
всех
полей в данной точке не зависимо от их
происхождения.
Рассмотрим некоторые частные случаи:
Бегущая волна. Постановка задачи: пусть имеются две волны, характеризующиеся векторами
 и имеющие одинаковые
и имеющие одинаковые
 и
.
и
.
 (I)
(I)
 (II)
(II)
Складываем почленно правые и левые части систем (I)+(II):
 (III)
(III)
При
этом суммы
 и
и
 будут давать напряженность и индукцию
результирующего поля, согласно принципу
суперпозиции. Т.о. (III)
можно записать:
будут давать напряженность и индукцию
результирующего поля, согласно принципу
суперпозиции. Т.о. (III)
можно записать:
 ,
,
г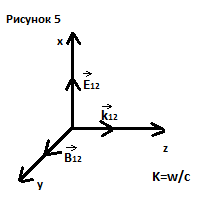 де
удовлетворяют принципу суперпозиции.
Возникает такая бегущая волна.
де
удовлетворяют принципу суперпозиции.
Возникает такая бегущая волна.
Биение. Постановка задачи: пусть две плоских электромагнитных волны с одинаковыми амплитудами E и B распространяются в одном направлении. Волны характеризуются частотами




В ыражение
для вектора В может быть получено
аналогичным способом. Амплитуда волны
может быть промодулирована
ыражение
для вектора В может быть получено
аналогичным способом. Амплитуда волны
может быть промодулирована
 – частота биения.
– частота биения.
Если
амплитуды одинаковы, то результирующее
колебание изменяется в пределах 0…2Е,
если амплитуды неравны, то изменяется
от
 до
до
 ,
м.б. использована для модулирования
радиосигнала.
,
м.б. использована для модулирования
радиосигнала.
Стоячие волны. Пусть имеются две волны с одинаковыми амплитудами и частотами, которые распространяются вдоль одной прямой в противоположных направлениях.
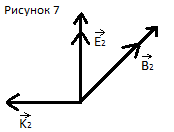 Из
рисунка следует:
Из
рисунка следует:
1)
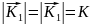
2)Вектора
 противонаправлены,
что тождественно сдвигу по фазе на
величину π.
противонаправлены,
что тождественно сдвигу по фазе на
величину π.
 ,
,
где
 – начальная разность фаз.
– начальная разность фаз.
 ,
(1)
,
(1)
где
 .
.
 не
является бегущей волной т.к. координата
(в данном случае z)
не входит в фазу, однако амплитуда волны
будет являться функция по z,
соответственно такая волна называется
стоячей.
не
является бегущей волной т.к. координата
(в данном случае z)
не входит в фазу, однако амплитуда волны
будет являться функция по z,
соответственно такая волна называется
стоячей.


Расстояние
между двумя соседними пучностями/узлами
 длина стоячей волны, причём
длина стоячей волны, причём
 .
Покажем, что в стоячей волне колебание
векторов
,
сдвинуты относительно друг друга по
фазе на величину π/2.
.
Покажем, что в стоячей волне колебание
векторов
,
сдвинуты относительно друг друга по
фазе на величину π/2.


 (2)
(2)
( 2)
содержит синусы, а (1) косинусы одних и
тех же аргументов. Отсюда следует что
вектора
,
смещены на π/2.
2)
содержит синусы, а (1) косинусы одних и
тех же аргументов. Отсюда следует что
вектора
,
смещены на π/2.
П лотность
потока энергии равна нулю в узлах и
пучностях. С течением времени энергия
двигается между соседними узлами и
пучностями, превращаясь из энергии
магнитного поля в энергию электрического
поля и обратно. Объемная плотность
энергии остается постоянной.
лотность
потока энергии равна нулю в узлах и
пучностях. С течением времени энергия
двигается между соседними узлами и
пучностями, превращаясь из энергии
магнитного поля в энергию электрического
поля и обратно. Объемная плотность
энергии остается постоянной.

1890
опыт Винера – экспериментальное
доказательство электромагнитных волн
света. При падении светового потока на
зеркало вблизи зеркала образуется
стоячая волна. Под углом α
к зеркалу расположена фотопластинка.
Почернения фотопластинки, возникшие в
ходе опыта, совпадают с пучностями
вектора
(вектор
в этих точках имеет узел). Расстояние
между почернениями примерно равны
 ,
то
есть совпадает с длиной стоячей волны.
Из опыта следует, что при взаимодействии
света с веществом основную роль играет
электрический вектор. В связи с этим
вектор
также еще называют световым вектором.
,
то
есть совпадает с длиной стоячей волны.
Из опыта следует, что при взаимодействии
света с веществом основную роль играет
электрический вектор. В связи с этим
вектор
также еще называют световым вектором.
§ Поляризация электромагнитных волн
Исторически
сложилось, что плоскость, содержащая
вектора
 ,
называется плоскостью поляризации, а
содержащая
,
называется плоскостью поляризации, а
содержащая
 — плоскостью колебаний (о ней, как
правило, будем говорить в дальнейшем).
— плоскостью колебаний (о ней, как
правило, будем говорить в дальнейшем).
 .
.
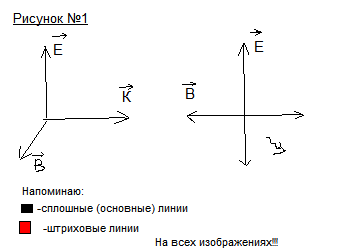 Если
в процессе распространения волны
плоскость колебаний сохраняет своё
положение, то волна называется плоско-
или линейнополяризованной.
Если
в процессе распространения волны
плоскость колебаний сохраняет своё
положение, то волна называется плоско-
или линейнополяризованной.
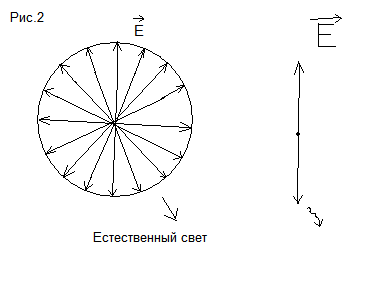
Рисунок 1. Волна от одного источника.
Рисунок 2. Результирующая волна от нескольких источников.(естественный свет). Выделяя из естественного света одну плоскость, получаем плоско-поляризованный свет.
 Рассмотрим
суперпозицию двух плоско-поляризованных
волн одинаковой частоты, распространяющихся
в одном направлении. Плоскости поляризации
взаимно перпендикулярны.
Рассмотрим
суперпозицию двух плоско-поляризованных
волн одинаковой частоты, распространяющихся
в одном направлении. Плоскости поляризации
взаимно перпендикулярны.
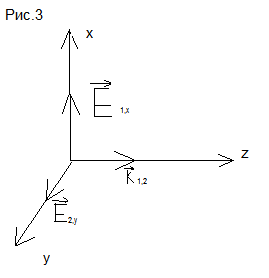

При сложении взаимно перпендикулярных гармонических колебаний получается колебание, вектор которого будет описывать эллиптическую кривую. Соответственно, в общем случае:

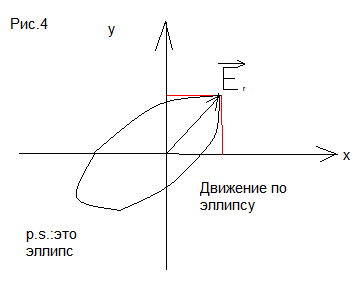 (1)
(1)
Уравнение описывает эллипс, произвольно ориентированный относительно осей.
1.
Рассмотрим частный случай.

a)

 (2)
(2)
–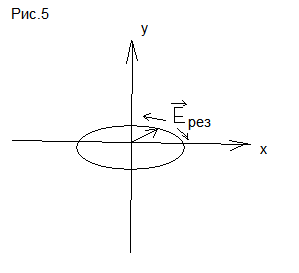 описывает
эллипс, оси которого совпадают с осями
координат.
описывает
эллипс, оси которого совпадают с осями
координат.
С уществует
два типа эллиптической поляризации:
если для наблюдателя, смотрящего
навстречу волне, вектор Е вращается
против часовой стрелки, то поляризация
называется левой, в противном случае 0
–правой.
уществует
два типа эллиптической поляризации:
если для наблюдателя, смотрящего
навстречу волне, вектор Е вращается
против часовой стрелки, то поляризация
называется левой, в противном случае 0
–правой.
б) -
круговая поляризация:
-
круговая поляризация:
 (3)
(3)
2)


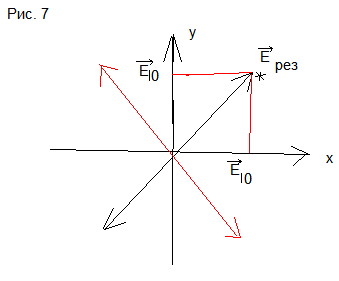 (4)
или
(4)
или
 –линейная.
–линейная.
Вышесказанное показывает, что электромагнитная волна с любым видом поляризации может быть представлена в виде суперпозиции двух взаимно перпендикулярных линейно-поляризованных волн. Также можно показать, что любая плоско-поляризованная волна может быть представлена в виде суперпозиции двух циркулярно-поляризованных волн. Т.о. В природе существует два вида поляризаций: эллиптическая и плоская, при этом они взаимно представимы.
