§ Электромагнитные волны (волновое уравнение)

Система уравнений Максвелла в дифференциальной форме имеет вид:

Параметры среды определяются следующими уравнениями: ; ; . Рассмотрим электромагнитные волны в вакууме. токов проводимости нет, ; . Исходя из чего получаем систему:

Электромагнитное излучение, подчиняющееся распространяется в виде электромагнитных волн, причем они могут распространяться в вакууме, при отсутствии среды.

( ) ; (5)

Применим к обеим частям выражения (5), операцию :

=> (grad div )= =>

(6)

По аналогии применяем к выражению ( ):

(7)

В курсе механики (см. волновые уравнения) аналогом величины 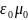была , где – скорость волны. Поскольку речь идёт о распределении света, , . С называется электродинамической постоянной.

Введем оператор Даламбера: . Тогда, волновые уравнения:

§ Плоские волны

Рассмотрим волновые уравнения для некоторой скалярной функции Ф(z,t), не зависящие от x и y. Уравнение плоской* волны выглядит следующим образом:

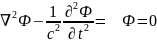(1)

*волна плоская, поскольку значение Ф при фиксированных z и t не зависит от x и y.

Используем новые независимые переменные:

(2)

Таким образом: (3)

(4)

(5)

(6)

В общем виде оператор Даламбера: (7)

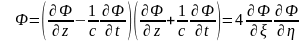(8)

Интегрируя (8) по , получаем функцию зависящую только от 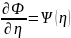(9)

Дальнейшее интегрирование приводит к: (10)

По ходу вычислений видно, что функции могут быть произвольными. С учетом (2) можно записать (11)

Покажем, что значение аргумента в точке в момент времени t совпадает со значением аргумента в момент времени .

, (12)

где

(13)

П ри выполнении условия (13) вид распространяющейся функции сохраняется, график для момента времени получается путем смещения графика момента на величину .

Можно ввести скорость . Аналогично можно показать, что функция 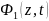может двигаться в отрицательном направлении на оси

Таким образом, обе функции описывают волну произвольной формы, которая перемещается, не меняя формы. Волна является суперпозицией 2 волн, двигающихся по оси в противоположных направлениях. Результат суперпозиции, как правило, трудно предсказуем.

§ Сферические волны

Е сли волна от точечного источника изотропна, то решение уравнения нужно искать в виде: .

(1)

– лапласиан в сферических коор-х в общем виде.

Значение функции в сферической поверхности не зависит от (волна изотропна), т.е. определяем только от :

(2)

(3)

Волновое уравнение 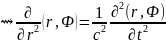(4)

Решение уравнения (4) можно записать по аналогии с функцией : z , ; (5)

(6)

По аналогии сходящаяся волна (т.е. сходится по радиусам к центру), расходящаяся волна.