§ Плоские гармонические волны. Волновой вектор

Если функции являются гармониескими функциями своего аргумента, то такая волна также считается гармонической.

(1)

Аналогично выражению (1) можно записать волну с использованием sin. Общее выражение для бегущей волны:

+В (2)

А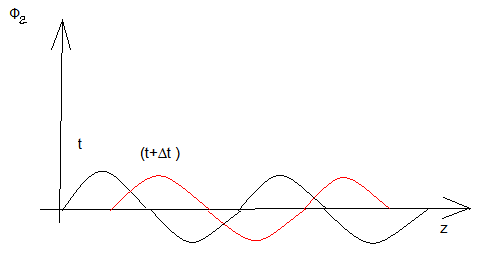 ргументы гармонических функций (1) и (2) называются фазами

(3)

С овокупность точек, колеблющихся в одинаковой фазе, образуют волновую поверхность.

Волновую поверхность, разделяющую возмущенную и не возмущенную области пространства, называют фронтом волны. Скорость движения фиксированной фазы волны называют фазовой скоростью:

Волновой фронт может как совпадать, так и не совпадать с волновой поверхностью.

Скорость распространения (фазовая) (4)

Дифференцируя по времени: =>

(5)

Фазовая скорость совпадает со скоростью света.

Выражение (4) можно представить в другом виде. Вводим понятие волнового числа: К= (6)

= (7)

+В (8)

У равнение волны в общем виде можно записать с помощью векторной величины. Вводится - волновой вектор. Его направление соноправлено со скоростью. ( ) Модуль его равен волновому числу . Если волна может распространяться произвольно:

Данная формула не зависит от системы координат и характеризует плоскую волну, распространяющуюся в направлении .

§ Представление гармонических волн в комплексном виде

Описание гармонических волн с помощью тригонометрии не всегда удобно в связи с математическими трудностями интегрирования и дифферинцирования, поэтому гармонические волны часто представляют в экспоненциальной форме. Основу переходов составляют формулы Эйлера:

Cоответственно . Значит плоская волна .

Cферическая волна = ,

где комплексная амплитуда. В случае наличия начальной фазы не равной 0.

§ Свойства элементарных и гармонических волн

Знаем, что gradU= ; div ; rot

Запись в комплексной форме: и (5)

; (6)

Подставляем выражение (5) в систему ( ) с учетом (6) и получаем:

Из и следует, что вектора , , взаимно перпендикулярны, следовательно, электромагнитные волны являются поперечными. Поперечность световых волн была открыта Юнгом в 1817 году. Благодаря этому он объяснил отсутствие интерференции во взаимно перпендикулярных плоскостях.

В озьмем модули от обеих частей уравнения : . Зная, что , или в общем случае

1. э-м волны поперечны;

2. вектора , , взаимно перпендикулярны и образуют право- винтовую систему;

3. вектора , софазны;

4. количественное соотношение между мгновенными значениями , : E=сВ.

§ Эффект Доплера

Классические формулы, описывающие эффект Доплера в механике имеют вид:

1. наблюдатель неподвижен, источник приближается ос скоростью v (

,

где ν – частота в системе источника,

u – скорость волны в неподвижной среде.

2. Наблюдатель неподвижен, источник удаляется (

.

3. Наблюдатель и источник двигаются со скоростями и соответственно

.

Чтобы эффект Доплера наблюдался в механике необходимо, чтобы расстояние между источником и наблюдателем постоянно менялось.

П усть источник света находится в системе , а приёмник в . Уравнение плоской световой волны, испускаемой источником по направлению к приёмнику в системе к имеет вид:

, (1)

где w – частота источника в k,

– начальная фаза.

Согласно принципу относительности, законы природы имеют одинаковый вид во всех ИСО, следовательно в системе волна будет описываться:

, (2)

где - частота в (та, которую принимает приёмник).

Уравнение волны в системе можно также получить из уравнения в системе , переходя от переменных x и t к с помощью преобразований Лоренца:

(3)

где . Это уравнение описывает ту же волну, но в системе . (2) аналогично (3)

=> (4) // //

При удалении от источника скорость > 0 и согласно (4) . Соответственно при приближении приемника к источнику скорость< 0 и . В общем случае, когда линия соединения источник-приёмник составляет угол φ с направлением перемещения (скорости), то

(5)

Выражения (4)- являются частным случаем (5) при φ = 0, они описывают продольный эффект Доплера.

При имеет место поперечный эффект Доплера: (6).

Из (6) видно, что частота принимаемая приёмником, падает.

ex. Источник движется по окружности, в центре которой находится приёмник. (В механике эффекта Доплера бы не наблюдалось).

Поперечный эффект Доплера является релятивистским эффектом, он связан с замедлением течения времени движущегося наблюдателя. Так, спектры галактик испытывают красное смещение.