Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2277.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

4.86 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3031 / 3131

Библиографический список

1.Шипачев, В.С. Высшая математика / В.С. Шипачев. М. : Высшая шко-

ла, 2012 . 479 с.

2.Карасева, Р.Б. Высшая математика дистанционно : учеб. пособ. /

Р.Б. Карасева. Омск : СибАДИ, 2008. Ч. 1. 148 с.
С				Математика: линейная алгебра, векторная алгебра, ана-
3. Карасева, Р.Б.
литическая геометрия, введение в математический анализ, дифференциальное
исчислен е функц			одной действительной переменной [Электронный ресурс] :
учебное пособ е / Р.Б. Карасева. – Электрон. дан. – Омск : СибАДИ, 2016. – Ре-
жим доступа: http://bek.sibadi.org/fulltext/esd106.pdf., свободный. – Загл. с экрана
методическое
(дата обращен я к ресурсу: 02.08.2019).
4.	Карасева,		Р.Б. Л нейная алгебра [Электронный		ресурс] : учебно-
		посо		/ Р.Б. Карасева. Электрон. дан.	Омск : СибАДИ,
2016.	134	. Реж		доступа: http://bek.sibadi.org/fulltext/esd216.pdf., свобод-
ный. – Загл.		пособ
		экрана (дата о ращения к ресурсу: 02.08.2019).
5.	Карасева,		Р.Б. Векторная алгебра [Электронный		ресурс] : учебно-
			/ Р.Б. Карасева. Электрон. дан. Омск : СибАДИ, 2016.
80 с. Реж м доступа: http://bek.sibadi.org/fulltext/esd217.pdf., свободный. – Загл.
с экрана (дата обращен				я к ресурсу: 02.08.2019).
6. Карасева, Р.Б.				Аналитическая
				геометрия [Электронный ресурс] : учеб-

ное пособие / Р.Б. Карасева. Электрон. дан. Омск : СибАДИ, 2017. 117 с.

Режим доступа: http://bek.sibadi.org/fulltext/esd310.pdf ., свободный. – Загл. с эк-

рана (дата обращения к ресурсу: 02.08.2019).

7.	Пискунов, Н.С. Дифференциальное и интегральное исчисление : учеб.
	Д
пособ. / Н.С. Пискунов. М. : Интеграл-Пресс, 2006. Т.1. 450 с.
8.	Данилов, Ю.М. Математика : учебное пособие / Ю.М.	анилов [и др.]. ;
ред. : Л.Н. Журбенко, Г.А. Никонова. М. : ИНФРА-М, 2016. 496 с.
9.	Письменный, Д.Т. Конспект лекций по высшей	математике /
Д.Т. Письменный. М. : Айрис-пресс, 2014. – Ч. 1. – 288 с.

10.Никольский, С.М. Курс математического анализа : учебник для вузов / С.М. Никольский. – М. : Физматлит, 2011. – 592 с.

11.Карасева, Р.Б.Дифференциальное исчисление функции одной действи-

		И
тельной переменной [Электронный ресурс] : учебное пособие / Р.Б. Карасева.
Электрон. дан. Омск : СибАДИ, 2018.		264 с. Режим доступа:

http://bek.sibadi.org/fulltext/esd597.pdf ., свободный. – Загл. с экрана (дата обра-

щения к ресурсу: 02.08.2019).

252

																			Приложение 1
										Виды матриц
		a				a	...			a
			11			12				1n
С													a
A a21						a22 ...				a2n			a		– матрица размерности m n,
						... ...				...			ij	m,n
		...				... ...				...
						am2 ...
		am1				am2 ...				amn
число													столбцов.
где m	− ч		сло строк; n						−				столбцов.
a11			a12			...	a1n
a21			a22			...	a2n			, А		m n– квадратная порядка п.
						... ...				n,n
... ...						... ...
a			бА
		n1		n2				nn
		1			0	0									1,		i j;
					1					( ij) ij					1,		i j;
E3 0					1	0 , En				( ij) ij								– единичная (квад-
					0										0,		i j
ратная).		0			0	1
ратная).		0			0	0
		0			0	0
					0						aij			0,		i, j– нулевая (размер про-
O 0					0	0 , O (0)					aij			0,		i, j– нулевая (размер про-
			0		0	0

извольный).
a			0			0
	11		a22						Dn (dij ) dij							0,		i j–	диагональная
	0		a22			0 ,			Dn (dij ) dij							0,		i j–	диагональная
	0		0										Д
	0		0			a33							Д
(квадратная).
a			a			a
	11		12			13			Tn	(tij ) tij					0		при i j–		верхняя тре-
	0		a22			a23 ,			Tn	(tij ) tij					0		при i j–		верхняя тре-
	0		0			a												И
						33
угольная (размер произвольный).
a			0			0
	11		a22						Tn (tij ) tij						0		при i j–		нижняя тре-
a21			a22			0 ,			Tn (tij ) tij						0		при i j–		нижняя тре-
a			a	32		a
	31			32		33

угольная (размер произвольный).

253

Приложение 2

Действия над матрицами

ложение (вычитание) матриц C A B.

Матрицы А и В должны иметь одинаковые размеры;

m,n

2. Умножен е матрицы на число C A.

матрица

Матр ца А

про звольного размера;

12 .

m,n

бА

1 A

A –

, противоположная матрице A.

3. Умножен е

C AB:

Соотношен е размеров:

= m

;

Cm,n Am,k Bk,n (ci j ) ( aik bk j ) (ai1b1j ai2b2 j aipbp j ).

Свойство: AB BA.

k 1

4. Транспонирование матрицы .

Матрица А

произвольного размера;

A a

– матрица размера m n,

i j

транспонированная матрица:

aji ,

имеет размер n m.

21 .

5. Прибавление к элементам одной строки (столбца) соответст-

вующих элементов другой строки (столбца), умноженной на число .

Размер матрицы произвольный.

a a

22 .

a21

a22

a21

a22

254

Приложение 3

Определители

Определителем квадратной матрицы порядка n 1 называется число

det A 1 k i aik Mik ,

k 1

где Mik – м нор порядка n 1 матрицы A, соответствующий эле-

менту a .

Сik

Определ тель 2-го порядка:

11 12

a21 a22

Определитель 3-го порядка:

а) разложение по 1-й строке:

a11

a12

a13

a22

a23

a21

a23

a21

a22

;

a31

a32

a33

б) по

бА

правилу Сарруса (треугольниками).

Перемножить выделенные элементы и выполнить указанные

сложения и вычитания:

a11

a12

a13

a a a

a21 a22

a23

─

a31

a32

a33

a11

a12

a13

a11

a12

a13

a11

a12

a13

─

a21

a22

a23

─

a21

a22

a23

─

a21

a22

a23 .

a31

a32

a33

a31

a32

a33

a31

a32

a33

255

		Приложение 4
	Обратная матрица
A 1	− обратная матрица к A a	, если
С		ij n,n
A A 1	A 1 A E.

Нахожден е обратной матрицы A 1:

1. Выч сл ть определитель матрицы A. (Если det A 0, то A 1

нения4. Умнож ть A на

не существует.)

остав ть матр

цу A Ai j

, где Ai j – алгебраические допол-

элементов ai j матрицы A.

бА1 1 1

3. Транспон ровать A.

~ T

det A

A .

det A

Свойства о ратной матрицы:

1. A

2. AB

;

3. AT

A 1

;

256

Приложение 5

Системы линейных уравнений

истема m линейных уравнений с n неизвестными:

a11x1 a12x2 a1nxn b1;
a x a			22	x	a	x	b ;
	21 1		22	2		2n n	2


a	x a	m2		x	a	x	b .
	m1 1	m2		2		mn n	m

a11

a12

a1n

a22

Матр ца коэфф ц ентов системы: A

a21

a2n

Столбец сво одных членов: B

Расширенная матрица системы: A*

бА

Матрица-столбец из переменных:

Метод Крамера решения крамеровских систем [число неиз-

вестных системы совпадает с числом уравнений (m n) и определи-

тель системы отличен от нуля]:

; x

; ; x

257

Окончание прил. 5

где det A 0, i – определитель, который получается из определителя системы, если в нем i-й столбец заменить столбцом свободных членов i 1, 2, ,n .

СМатричный метод решения крамеровских систем [число неиз-

вестных с стемы совпадает с числом уравнений (m n) и определи-

тель с стемы отл чен от нуля]: матрицы X A 1B.

Метод Гаусса решения произвольных систем.

Пр веден е расширенной матрицы системы с помощью эле-
– умножатьбавлятьстроки матрицы A* на любые числа, кроме нуля;
ментарных прео разований, производимых только над строками этой
к трапец ев дному виду.
Разрешаются элементарные преобразования:
– пр	к лю ой строке другую строку, умноженную на
любое ч сло;	А

– переставлять строкиA*;

– вычеркивать одну из двух пропорциональных строк;

– вычеркивать нулевую строку.
Возможные результаты:						Д
Возможные результаты:
а)	0			система имеет единственное решение (совмест-
на);						И

б)	0
					система имеет бесконечно много решений (со-


вместна);

	0	1
в)	0=	1	система противоречива, решений не имеет (несо-
в)			система противоречива, решений не имеет (несо-

вместна).

258

Приложение 6

Ранг матрицы

Ранг матрицы А – наибольший порядок минора этой матрицы, Сотличный от нуля. Обозначение: r A , rang(A).

Элементарные преобразования, не меняющие ранга матрицы:

строки
–	перестановка строк матрицы;
–	вычерк ван е строки, все элементы которой равны нулю;
–	умножен е какой-ли о строки на число, отличное от нуля;

– пр бавлен е к элементам одной строки соответствующих эле-

ментов другой	;
– те же операц	со стол цами.

Теорема Кронекера–Капелли (критерий совместности системы линейных уравнен й): для совместности системы линейных уравне-

ний необходимо и достаточно, ранг матрицы системы был ра-

чтобы

вен рангу расширеннойАматрицы системы: r A r A*.

Если система совместна т. е. r A r A* , то возможны случаи: а) r A r A* r n (ранг равен числу неизвестных). Система m линейных уравненийДс n неизвестными совместна,

определена, имеет единственное решение.

б) r A r A* =r n (ранг меньше числа неизвестных). Система m линейных уравнений с n неизвестными совместна,

определена, имеет бесконечно многорешений. И

259

						Приложение 7
обственные векторы, собственные значения матрицы
A квадратная матрица;			X неизвестный числовой вектор;
С
неизвестное число.
обственные значения матрицы A ─ нетривиальные решения
уравнен я	AX X ; собственные векторы ─ нетривиальные
решен я Х.
или
Нахожден е со ственных чисел: составить и решить характе-
ристическое уравнен е
		det A E 0,

	А
	a11	a12			a1n
	a21	a22			a2n	0.
	б					0.

	an1	an2		ann
			Д
					И

260

Приложение 8

Операции над векторами

ложение:

число

0 a

2. Выч тан е:

( b

3. Умножен е на

;

1 2

бАn 1 1 2 2 n n

;

4. Линейная комбинация векторов

a1,

2, ,

с коэффициента-

ми , , , : вектор

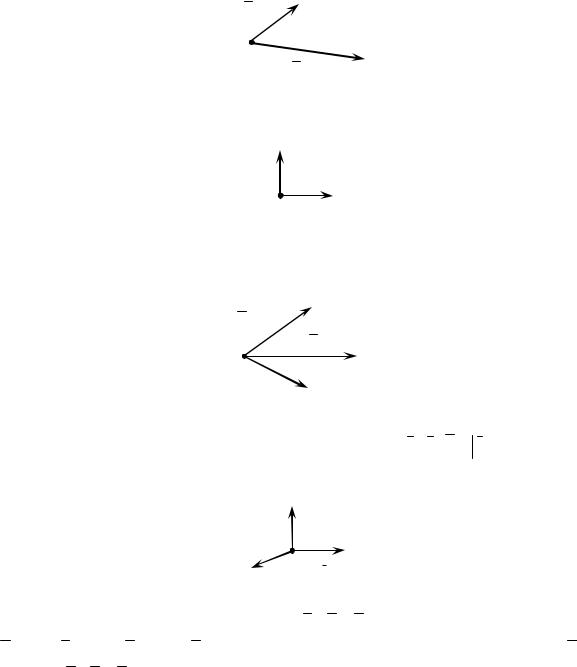
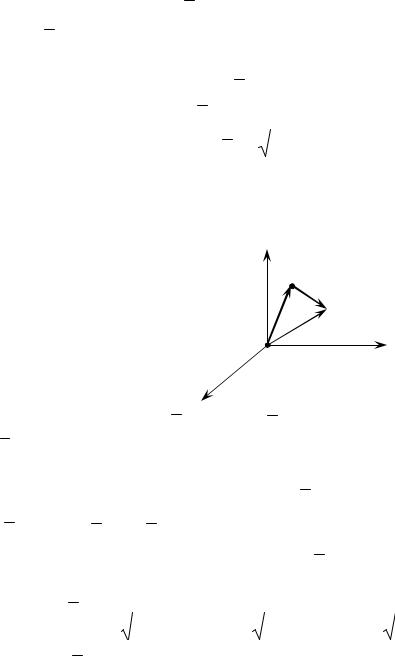
5. Проекция вектора а Вна ось U :

Ось

В1

А1
а) A1B1 геометрическая проекция вектораИAB на ось U .
	A1B1 ,если A1B1 U;	– алгебраическая
б) число ПрU AB	A1B1 ,если A1B1 U;	– алгебраическая
	A1B1 ,если A1B1 U

проекция AB на ось U .

261

Приложение 9

Базис и координаты

Базис на плоскости – любые два неколлинеарные вектора:

тандартный баз с на плоскости – i, j :

1, i j:

любые

Баз с в пространстве это

три некомпланарные векто-

ра в пространстве.

Стандартный базис в пространстве i, j,

k :

j k .

Координаты вектора. Если

e1,

3 базис в пространстве, то

e1 2

2 3

3 1, 2, 3 .

1, 2, 3 координаты

базисе

e1,

3 .

262

Приложение 10

Действия с векторами в координатной форме записи

1.умма векторов – это вектор с координатами


					a	b	x1 x2; y1 y2;			z1 z2 ,
если	а	x1, y1, z1 ;	b	x2, y2, z2 .
	2. Умножен е вектора на число :
								a	x; y; z .

Дл на вектора

x, y, z :

x2 y2 z2

4. Коорд наты вектора

бА

x2 x1

;

y1 ;

z1 ,

A x1,

y1, z1 ;

B x2,

y2, z2 две точки.

Орт вектора

: вектор

о, имеющий то же направление, что и

, и модуль, равный 1:

а ,

x, y, z :

5. Координаты орта вектора

а)

;

x2 y2

x2 y2 z2

б)

cos ,cos ,cos ,

т.е. координаты орта равны направ-

ляющим косинусам.

Основное свойство направляющих косинусов вектора: cos2 cos2 cos2 1.

263

Приложение 11

Скалярное произведение

калярное произведение векторов

и b – число

С2

cos

проекц

или

на

Пр

Кр тер й ортогональности векторов:

сполВыч слен ескалярногоьзованиепроизведения: a b x1x2

y1 y2 z1z2,

Основное

а)

;

нахождение длины вектора;

бА

б)

cos

нахождение угла между векторами.

если

x1, y1, z1

b x2, y2, z2 .

Векторное произведение векторов

Векторное

произведение

векторов

– вектор

[

]

со свойствами:

sin

длина векторного произведения;

вектор с перпендикулярен плоскости векторов

и b;

расположен по отношениюДк векторам a и

так же, как

ось

к осям

Критерий коллинеарности:

Основное использование:

а) Sпар

– вычисление площади параллелограмма;

б) S

– вычисление площади треугольника.

264

Окончание прил. 11

Вычисление векторного произведения векторов:

x2, y2, z2

x1,

y1, z1

если

спользованиОсновное

е:

Смешанное произведение векторов

мешанное про зведение векторов

– число

Кр тер й компланарности: векторы

компланарны

тогда только тогда, когда

а) Vпар

– о ъём параллелепипеда, построенного на век-

торах

,c ;

б) V

– о ъём пирамиды, построенной на векторах

пир

ВычислениебАсмешанного произведения векторов через их коор-

динаты:

b c

где

xa ,

ya, za ;

xb,

, zb ;

xc , yc, zc

координаты

векторов.

265

Приложение 12

Точки пересечения линий

Чтобы выяснить, есть ли у двух линий f1 x, y 0 и f2 x, y 0 общие точки, составляется система

Расстояние		x, y 0;
С	f1
		x, y 0.
	f2

	бА
			между двумя точками
Расстоян е между точками A1 x1; y1 и A2 x2;y2 вычисляется по
формуле			x2 x1 2 y2 y1 2 .
	d		x2 x1 2 y2 y1 2 .
	Координаты точки середины отрезка
				Д
	(		x1 x2		,	y1 y2	).
			2			2
Координаты точки, делящей отрезок в отношении 0
		x1 + x2				y1 + y2		И
	(		1+		,	1+		).

Способы задания линии на плоскости

1.y f x явный;

2.x, y 0 неявный;

3.r r t векторный;

4. x x t ;	параметрический.
y y t .

266

					Приложение 13
					Прямая на плоскости
			Виды уравнения прямой на плоскости
С
1.	y kx b – уравнение прямой с угловым коэффициентом
(для прямых, не параллельных оси Oy).
и0						– по-
2.	Ax By C 0 общее уравнение прямой (где A,B,C
стоянные, пр чем A2 B2 0).
3.	r	r0		а	t векторное уравнение.
4.	x x		lt;
					параметрическое уравнение прямой;
	y y0		mt

x0, y0 – координаты точки на прямой;

,m – координаты направляющего вектора.

y y0

x x0

уравнение прямой, проходящей через две

y1 y0

x1 x0

заданные точкиб. А

1 уравнение прямой «в отрезках».

a b

Расстояние от точкиM0 x0, y0 до прямойAx By C 0

Ax0 By0 C

A2 B2

267

									Окончание прил. 13
	Угол между прямыми
1 :	y k1 x b1;						2 : y k2 x b2 .
С							k2 k1		.
С
	tg	,
	tg	,
	1			2		1 k k		2
Условие						1		2
Условие
	параллельности прямых
	1 \|\|		2		k1 k2 .
бА
Услов е перпендикулярности прямых
	1 2 k1 k2 1.
				Д
									И

268

Приложение 14

Кривые второго порядка

Общее алгебраическое уравнение второго порядка на плоско-

С
сти
	ax2 +bxy +cy2 + Ax + By +C = 0.
и			Эллипс
			Эллипс
	Связь параметров эллипса
бА
	a2			c2		b2 .
Канон ческое уравнен е эллипса с центром в начале координат
		x2			y2		1.
		a2			b2		1.
				Д
Уравнение эллипса с центром в точке x0								, y0
	x x0 2			y y0 2 1.
	a2						b2
							И
Уравнение окружности с центром в точке								x0, y0

x x0 2 y y0 2 R2.

Параметрическое уравнение эллипса с центром в начале координат

x acost;

y bsint.

269

Окончание прил. 14

Параметрическое уравнение окружности с центром в начале координат

x Rcost;

y Rsint.

	Эксцентриситет эллипса
Оптическое
Оптическое
С		;	b	2	, 0 эл 1.
		;	1		, 0 эл 1.
	a		a
бА
			свойство эллипса

Лучи света, сходящие из одного фокуса эллипса, после зеркального отражен я от эллипса проходят через второй фокус.

Д И

270

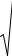
Приложение 15

Гипербола

Связь параметров гиперболы

c2 a2

b2 .

Канон ческое уравнен е гиперболы с центром в начале координат

(

направлены вправо и влево)

ветви

бА

x0, y0

Уравнен е г пер олы с центром в точке

(ветви направлены вправо и влево)

x x0 2

y y0 2

(ветви направлены вверх и вниз)

x x0 2

y y0 2

Эксцентриситет гиперболы

;

; гип 1.

Оптическое свойство гиперболы

Лучи света, исходящие из одного фокуса гиперболы, после зер-
кального отражения от гиперболы идут так, как если бы они вышли из
второго фокуса.	И

271

					Приложение 16
			Парабола
	Каноническое уравнение параболы с вершиной в начале коор-
С
динат
			y2 2px
(при p 0 ветви параболы направлены вправо;				при	p 0	ветви на-
	при
правлены влево);
			x2 2py
(	p 0 ветви пара олы направлены вверх;			при	p 0	ветви на-
	бА
правлены вн з).
	Уравнен е пара олы с вершиной в точке x0, y0
		y y0 2 2p x x0 .
	Эксцентриситет параболы пар 1.
			Д
		Оптическое свойство параболы
	Лучи света, исходящие из фокуса параболы, после зеркального
отражения от параболы идут параллельно оси параболы.
			И

272

			Приложение 17
		Плоскость
С				x0, y0,z0
Уравнение плоскости, проходящей через точку M0				x0, y0,z0
перпенд кулярно вектору	n	A,B,C :
и			0.
A x x0 B y y0 C z z0			0.
О щее уравнение плоскости
бА
Ax By Cz D 0,

где A,B,C коорд наты нормали плоскости.

Уравнение плоскости, проходящей через три заданные точ-

ки: M1 x1,y1,z1 , M2 x2, y2,z2 и M3 x3, y3,z3 :

	x x1	y y1	z z1
	x2 x1	Д
	x2 x1	y2 y1	z2 z1	0.
	x3 x1	y3 y1	z3 z1
Уравнение плоскости в отрезках
	x	y	z	И

a + b + c =1.

Угол между двумя плоскостями

A1x + B1y +C1z + D1 = 0 и A2x + B2 y +C2z + D2 = 0:

cos	n1 n2			A1 A2 B1 B2 С1С2					.
cos	n1 n2								.
	n1 n2		A2	B2	С2	A2	B2	С2
		1		1	1	2	2	2

273

Окончание прил. 17

Условие параллельности плоскостей

Услов е перпендикулярности плоскостей

1 2 n1 n2 A1A2 + B1B2 +C1C2 = 0.

Расстоян е от точки M x1, y2,z1 до плоскости
Ax By Cz D 0:
бА
Ax	By	Cz	D
и1	1	1
d					.
	A2 B2 C2
	Д
				И

274

Приложение 18

Прямая в пространстве

Каноническое уравнение прямой в пространстве, проходящей

через точку M0 x0, y0,z0 параллельно вектору

,m,n :

x x0

y y0

z z0

Уравнен е прямой в пространстве, проходящей через две точки:

M1 x1

,y1,z1 , M2

, y2

,z2

бА

x x1

z z1

y2 y1

z2 z1

Уравнение

прямой

как

система

уравнений двух непарал-

лельных плоскостей

A1x B1y C1z D1 0;

A x B y C

z D 0.

Взаимное расположение прямых в пространстве

Даны канонические уравнения прямых в пространстве:

x x0

y y0

z z0

x x0

z z0

;

Дl :

Тогда

а) l //l

, т.е. l //l

;

б) l1 l2

1 2 +m1m2 +n1n2 = 0;

в) cos =

1 2 + m1 m2 + n1n2

– угол между

a1 a2

2 + m2

+ n2

+ m2 + n

прямыми.

275

Приложение 19

Взаимное расположение прямой и плоскости

в пространстве

y y0

z z0

а) Прямая

x x0

// плоскости

Ax By Cz D 0

,m,n

A,B,C ,

т.е. если

б) прямая

плоскости при условии n//a, т.е.

;

бА

m n

в) угол между прямой

плоскостью

sin

A Bm Cn

A B

276

Приложение 20

Поверхности второго порядка

Название

Вид

Эллиптический ци-

линдр

Гиперболический

ц л ндр

Парабол ческ й

x2 = 2py

гиДвуполостный -

ц л ндр

фера

(x x0 )2 (y y0 )2 (z z0 )2

Элл псо д

перболо

Однополостный

перболо д

Элл пт ческ й па-

2z,

где p 0;q 0

раболоид

Гиперболический

параболоид

Конус

второго по-

рядка

277

Приложение 21

Символы и обозначения

| | – знак параллельности

– знак «Не принадлежит»

– знак перпендикулярности

– знак включения

– знак объединения

– знак следования

– знак равнос

льности (эквивалентно-

– знак пересечения

сти)

Определения

– знак приближённого равенст-

– знак пр надлежности

ва

Множества.

этого понятия нет. Под множеством

быть

будем пон мать совокупность некоторых объектов. При этом множе-

ство должно

оп сано так, чтобы можно было понять, принадле-

жит тот ли ной о ъект данному множеству или нет. Описать то или

иное множество можно, например, перечислением его элементов или

описанием характерных свойств элементов.

Множество, не содержащее ни одного элемента, обозначается

символом – пустое множество.

Числовые множества.

N 1,2,3,...,n,... – множество натуральных чисел;

Z 1, 2, 3,..., n,... – множество целых чисел;

Q =

; m N; n N – множество рациональных чисел;

I – множество иррациональных чисел – чисел, не являющихся рацио-

нальными. Такие числа можно представить в виде бесконечной непе-

риодической десятичной дроби;

R Q I – множество действительных чисел.

Числовые промежутки представляют собой подмножества

множества R:

a x b ; интервал a,Иb x R a x b ;

отрезок a,b x R

полуинтервалы

a,b

x R

a x b ; a;b x R

a x b ;

бесконечные промежутки

a, x R

x a ;

a; x R

x a ;

;a x R

x a ;

, a x R

x a ;

, R

вся числовая ось.

278

Приложение 22

Основные алгебраические соотношения

Действия со степенями

a n

a0 1

n b

am an am n

am n

m n

m n a m n a

n a b n a n b

Сa b a b

n am an

Действ я с логар

(

>0; a 0)

alogab

logac

loga b

loga b loga c logc b

фмами

logaa 1;

loga1 0

loga b c loga b loga c

loga b

logc b

logc a

lna b a eb

loga

loga b loga c

lga log10 a

loga bc cloga b

loga b

lna loge a

logb a

бА

Формулы сокращенного умножения

a b 2 a2 2ab b2

a2 b2 a b a b

3ab

a3 b3 a b

a2 ab b

Корни квадратного уравнения ax

bx c

b2 4ac

1,2

трехчлена на множители

Разложение квадратного

bx c a x x1 x x2

, где x1, x2

– корни уравнения.

ax2 bx c 0.

Выделение полного квадрата в квадратном трехчлене

	2		p 2	p 2
x		px q x			q
			2	2

279

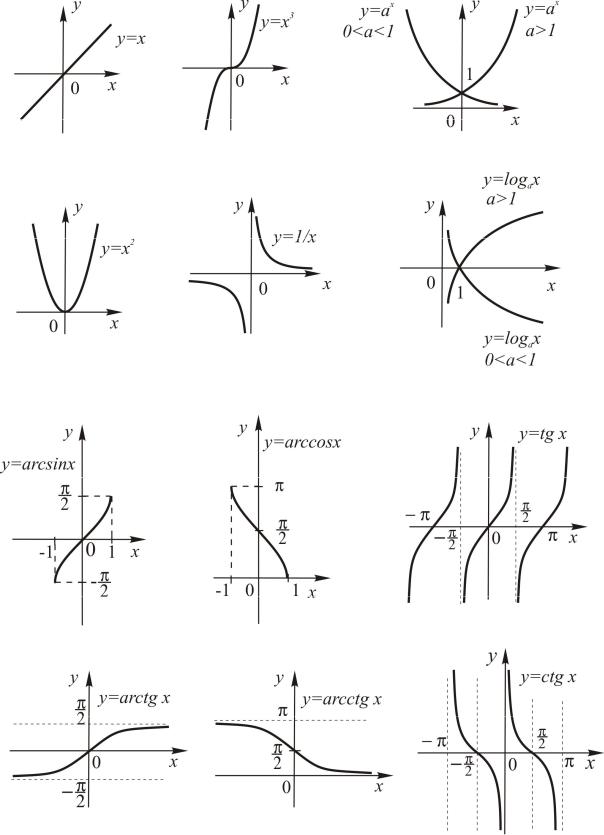
Приложение 23

Графики элементарных функций

Си бА Д И

280

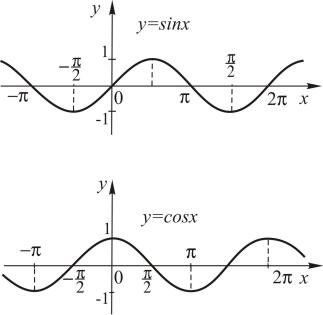
Окончание прил. 23

С
и
	бА
	Четные и нечетные функции. Функция f x называется чет-
ной, если для всех		x из о ласти ее определения выполняется равен-
ство		Д
		f x f x .
	Характерной особенностью графика четной функции является
то, что он симметричен относительнооси ординат.
	Функция f x	называется нечетной, если для всех x из области
ее определения выполняется равенство
		f x f x .
	График нечетной функции симметричен относительно начала
координат.			И

Например, функция f x cosx является четной, функция f x sinx является нечетной.

281

Приложение 24

Основные тригонометрические соотношения

sin2 cos2 1

tg ctg 1

cosα

sin

ctg

cos

sinα

1 tg2

1 ctg2

cos2

sin2

sin( ) sin

cos( ) cos

умма

разность двух аргументов

sin sin cos cos sin

cos cos cos sin sin

tg tg

ctg

ctg tg 1

tg tg

ctgα ctg

Двойные аргументы

sin2 2sin cos

cos2 cos2 sin2

2tg

Д2

tg2

ctg2

ctg2 1

б1 tg α А2ctgα

Формулы понижения степени

sin2

1 cos2

cos2

1 cos2

Преобразование произведения в сумму

sin sin

cos

cos cos 12 cos cos

sin cos 12 sin sin

282

Окончание прил. 24

Преобразование суммы и разности в произведение


С
	sin sin 2sin										cos						sin sin 2cos								sin
	sin sin 2sin										cos						sin sin 2cos								sin
								2					2							2								2
	cos cos 2cos									cos							cos cos 2sin									sin
	cos cos 2cos							2		cos			2				cos cos 2sin									sin
								2					2							2								2
	и
	tg tg			sin													tg tg			sin
			cos cos																	cos cos
	Некоторые значен я тр гонометрических функций
			бА
		0			6					4				3			2	2 3		3 4				5 6
	sin	0			1 2						2	2			3	2	1	3	2	2		2		1 2					0
	cos	1				3	2		2 2					1 2			0	1 2			2		2			3	2		1
		0			30						45			60			90	120		135				150					180

Тригонометрические уравнения1
sin x a; x 1 k arcsina k	Д
sin x a; x 1 k arcsina k	cos x a; x arccosa 2 k
tg x = a; x = arctg x+ k	ctg x = a; x = arcctg x+ k	k Z
	И

283

Приложение 25

Предел функции

Два определения предела функции

Число А называется пределом функции y f x в точке а (или

при x a), если для любого числа 0

существует число 0 (за-

висящее от ), такое, что при всех х, удовлетворяющих неравенству

x a

, выполняется неравенство

f x A

сло А называется пределом функции y f x в точке а, если

для любой

xn , такой, что lim xn a, выполня-

ется lim f

xn A.

последовательности

Основные свойства пределов функции

1. Если предел функции при стремлении к a существует, то он

единственный.

2. Если в некоторой окрестности точки а выполняется неравен-

ство f x g x и lim f x A;

lim g x B, то A B.

x a

3 (О двух милиционерах).

Если в некоторой окрестности точки

выполняется

неравенство

f x x g x

бА

lim f x lim g x A, то

lim x A.

x a

4. Пусть lim f x A; lim g x B, тогда

x a

1)lim f x g x A B;

x a

lim f x g x AB;

x a

f x

3) если B 0, то lim

;

x a g x

lim С f x C A, где С число;

x a

5)lim f x g(x) AB.

x a

284

Окончание прил. 25

5 ( вязь бесконечно малых и бесконечно больших функций).

1) если lim f x 0, то lim

;

x a

2) если lim f x , то lim

f x

x a

;

Если

СПредел функции на бесконечности

для лю ой xn

п.

. .,

lim f xn A, то

lim

f x A

(предел f x на равен A).

. xn lim f xn A, то

f x A

Если для лю ой о.

lim

(предел

f x на равен

A).

бПредел функции равен бесконечности

Если для лю ой п. .

. последовательности xn последователь-

ность f x также п. б. б., то lim

f x .

Правило Лопиталя (раскрытие неопределенностей типа

;

)

Пусть функции f(x), g(x) определеныД, непрерывны и дифферен-

цируемы в точке x0 и некоторой ее окрестности, причем g'(x)

0 для

любого x из этой окрестности, и пусть f(x), g(x) – бесконечно малые

при x x0.

Если предел

lim

f (x)

существует, то существует и

g (x)

x x0

f (x)

предел

lim

f (x)

, причем

lim

f (x)

lim

x x0 g(x)

x x0

g (x)

285

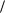
Замечательные пределы

Приложение 26

sin x

1. lim

первый замечательный предел.

x 0

Сa

2. lim

e второй замечательный предел;

lim 1 x 1 x

x 0

3. lim

log

1 x

x 0

бА

lim

ln 1 x

1 частный случай.

x 0

4. lim

ax 1

x 0

ex 1

lim

1 частный случай.

x 0

arcsinДx arctg x

5. lim 1 x 1 .

x 0

tg x

lim

1; lim

x 0

x 0 x

Таблица эквивалентных функций

1) sin ~

;

2)Иtg ~ ;

3) arcsin

;

4) arctg

~ ;

5) ln 1 ~ ;

6) e 1 ~ ;

7) 1 n 1 ~ n ;

8) a 1~ lna.

286

Приложение 27

Непрерывность функции

Развёрнутое определение непрерывности

Функция y f x является непрерывной в точке а, если

1) определено значение функции в точке а;

существуют конечные односторонние пределы

lim

f x ; lim f x ;

эти

x a

lim f x lim

f x ;

эти пределы равны между собой:

x a

пределы равны f (a): lim f x lim

f x f a .

x a

Свойства непрерывных функций

1. Если f x

g x непрерывны в точке а, то

f x g x сумма (разность) непрерывна в точке а;

f x g x произведение непрерывно в точке а;

f x

отношение

непрерывно

в точке а при условии

g x

g a 0.

2. (НепрерывностьбАсложной функции). Если y x непрерыв-

на в точке а и

z f y

непрерывна в

точке

b a ,

то сложная

функция z f x непрерывна в точке а.

Теорема ВейерштрассаД

Если функция непрерывна на отрезке a;b , то она достигает на

этом отрезке

своего

наименьшего

наибольшего

значений:

x1,x2 a,b : f x1 m,

f x2 M .

Теорема Коши

Если функция непрерывна на отрезке a;b , то она принимает все промежуточные значения между наибольшим и наименьшим зна-

чениями: k m,M x0 a,b : f x0 k.

287

			Окончание прил. 27
Точки разрыва графика функции
Точка, в которой нарушено хотя бы одно из четырех условий
непрерывности, называется точкой разрыва графика функции.
Точка а называется точкой разрыва первого рода, если условие
2 развернутого определения непрерывности функции не нарушено.
С
y		y
f a		y
иx			f a
иx				x
a			a	x
a

Точка разрыва а называется точкой разрыва второго рода, ес-
ли нарушается условие 2 непрерывности функции.
y бА
		y
	x		x
		Дa
		И
		288

Приложение 28

Определение производной

f (x 0) lim

lim

f (x0 x) f (x0 )

lim

f (x) f (x0)

x 0 x

x 0

x x0

Геометрический смысл производной

f (x0) = k = tg .

f (x) в точке x0

равна угловому коэффи-

Про зводная функции

касательной к графику y = f (x) в точке с абсциссой x0.

Уравнение касательной

циенту

y – f (x0) = f (x0)(x – x0).

Уравнение нормали

y – f (x0) =

(x – x0).

f (x0

)

бА

Механический смысл производной

V(t

) lim

S (t

t 0

Производная от S = S(t) в момент времени t0 есть скорость в мо-

мент времени t0.

Дифференцирование параметрически заданных функций

yx yt ;

x (t).

289

Приложение 29

Таблица производных

1. c 0.

9. arcsinx

1 x

2. xm mxm 1;

10. arccosx

3. a

1 x2

lna;

11. arctgx

1 x2

ex ex.

бА

4. loga x

;

иxlna

12. arcctgx

1 x2 .

lnx

cosx.

13. (shx)' = chx.

5. sinx

14. (chx)' = shx.

6. cosx

sinx.

7. tgx

15.

(thx)

ch2 x

cos2 x

8. ctgx

Д16. (cthx) .

sin

u v uv

;

u v uv

;

yx = yu ux .

290

Приложение 30

Основные теоремы о дифференцируемых функциях

Теорема Ферма. Пусть функция f (x) определена, непрерывна на интервале (a, b) и в некоторой точке x0 этого интервала принимает свое наибольшее или наименьшее значение. Если в точке x0 существует про зводная этой функции, то f (x0 ) = 0.

Теорема Ролля. Если функция f (x) непрерывна на отрезке [a, b],

руема в каждой точке интервала (a, b) и f (a) = f(b), то
С	отрезка [a, b],
существует по крайней мере одна внутренняя точка x0
такая, что f ' (x0) = 0.

Теорема Лагранжа. Если функция f (x) непрерывна на отрезке
[a, b], д фференц руема на интервале (a, b), то найдется хотя бы одна
дифференц
внутренняя точка x0 отрезка [a, b], такая, что верна формула
f (x0 )=	f (b) f (a).
	b a
Формула Лагранжа.		f (b) – f (a) = f (x0)(b – a).
Признак постоянства функции. Если функция f(x) непрерывна
	бА		f	(x) = 0,
на отрезке [a, b] и во всех внутренних точках этого отрезка			f	(x) = 0,
то функция f (x) постоянна на отрезке [a, b].

Теорема Коши. Пусть функции f (x), g (x) непрерывны на отрез-
ке [a, b], дифференцируемы на (a, b), причем f '(x) 0 для любой точ-
			Д
ки x из интервала (a, b). Тогда существует внутренняя точка x0 отрезка
[a, b], такая, что	f (b) f (a)	=	f (x0)	.	И

(b) (a)			(x0)

291

						Приложение 31
				Дифференциал функции
С				d f(x) = f (x) dx,
С
Формулы для приближенных вычислений с помощью
дифференц ала
функцииД фференц ал					f(x) в точке x0 равен приращению орди-
			f	(x x0 ) f (x0		) f (x0 ) x;
				y f (x0) x.
	бА
Геометр ческий смысл						дифференциала df (x0)
наты касательной.
		Свойства дифференциала функции
1. d (u + v) = du + dv.
2. d (u v) = u dv + v du.
3. d	u	= du v u dv			(v 0).
3. d		= du v u dv			(v 0).
v				v2		И
				ДифференциалДn-го порядка

d ny = f (n)( x) dx n.

292

Приложение 32

Исследование функции и построение графика


	Необходимое условие монотонности функции
СX							X
а) Если дифференцируемая функция f					(x) монотонно возрастает
на промежутке X		производная	f (x)		существует	на	X ,		то
f (x) 0; x X .
Если					f (x) монотонно убывает
б)	д фференцируемая функция				f (x) монотонно убывает
на промежутке		производная	f	(x)	существует	на		,	то
f (x) 0; x X .


бА
Достаточное условие монотонности функции
а) Если f (x) – д фференцируемая на X		функция и	f (x) 0;
x X , то f (x) монотонно возрастает на X .			f (x) 0;
б) Если f (x) – дифференцируемая на X		функция и
x X , то f (x) монотонно у ывает на X .
Необходимое условие экстремума
	Д
Если дифференцируемая в точке x c функция y f			(x) имеет
экстремум в этой точке, то f (c) 0.
	И
Достаточное условие экстремума
Пусть функция y f (x)	непрерывна, дифференцируема во всех
точках некоторого интервала,	содержащего точку x c, за исключе-

нием, возможно, самой точки c. Если при переходе аргумента через критическую точку с первая производная меняет знак, то данная критическая точка 1-го рода является точкой экстремума.

293

Продолжение прил. 32

Достаточный признак существования экстремума, основанный на второй производной

С				критическая точка для функции y f (x), причем
Пусть x c –
f (c) 0. Тогда
а) если			f (c) 0, то x c – точка локального минимума;
б) если			f (c) 0, то x c – точка локального максимума.
Если
Прав ло определения направления выпуклости графика
функц	Необходимоеусловие существования точек перегиба
а)
			f (x) 0		во всех внутренних точках Х, то функция
y f (x)		выпукла вверх на Х;
б) Если			f (x) 0		во всех внутренних точках Х, то функция
y f (x)		выпукла вн з на Х.
				А
Пусть график функции y f (x) имеет перегиб в точке с. Если
функция		y f (x)			Д
				имеет непрерывную вторую производную, то
f (c) 0.
Достаточное условие существования точки перегиба
					И

Пусть функция y f (x) непрерывна, дважды дифференцируема во всех точках некоторого интервала, содержащего точку x c, за исключением, возможно, самой точки c. Пусть x c – критическая точка 2-го рода. Если при переходе аргумента через точку с вторая производная функции меняет знак, то данная критическая точка 2-го рода является точкой перегиба.

294

Окончание прил. 32

Асимптоты графика функции

Прямая x a			называется вертикальной асимптотой кривой
С				f (x) или lim				f (x) .
y f (x), если		lim
		x a 0					x a 0
Прямая		y =	kx+	b	является		наклонной асимптотой кривой
y f (x),		k lim			f (x)	;	b lim	( f (x) k x) .

еxсли							x
			x		x
Прямая y b является горизонтальной асимптотой, если
1.	Найтиобластьопределения функции.
k lim	f (x) 0; b lim f x 0.
x				x
	Схема	сследования функции и построения графика
2.	Выяснить, является ли функция чётной, нечётной или общего
вида.						Д
3.
	Найти точки пересечения графика с осями координат.
4.	Найти асимптотыАграфика функции (вертикальные, горизон-
тальные, наклонные).
5.	Найти первую производную функции. Определить интервалы
возрастания, убывания, точки экстремума функции.
6.								И
	Найти вторую производную функции. Определить интервалы
выпуклости (вогнутости) и точки перегиба графика функции.
7.	На основании проведённого исследования выбрать масштаб,
построить график функции.

295

Формула Тейлора

Приложение 33

f (x) = f (x0) +

f (x0)

(x – x0) +

f (x0)

(x – x0) 2 +...+

f (n) (x0)

(x – x0) n +Rn(x)

(Rn(x) – остаточный член).

Формы остаточного члена

Коши n!

Форма Лагранжа: Rn(x) =

f (n 1)(с)

(x – x0)

n+1

, где

c – некоторое число,

(n 1)!

заключенное между x0

бА

Форма

: Rn(x) =

(n 1)

(x x

))

(x – x0) n+1(1 – ) n,

где удовлетворяет неравенству 0 <

< 1.

Формула Маклорена

f(x) = f(0) +

f (0)

x +

f (0)

x2 + ... +

f (n)(0)

xn + Rn(x),

(n 1)

где Rn(x) =

( x)x n+1 ,

(0 < < 1)

– остаточный член в форме

(n 1)!

Лагранжа.

Разложения некоторых элементарныхДфункций по формуле

Маклорена

ex = 1 +

+ ... +

xn 1

e x;

0 < < 1;

(n 1)!

m x2m 1

m+1 x2m 3

sin x = x –

– ... + (–1)

+ (–1)

cos x;

(2m 1)!

(2m 3)!

x2m

m+1

x2m 2

сos x = 1 –

– ... + (–1)

+ (–1)

cos x.

(2m)!

(2m 2)!

296

ТРЕБОВАНИЯ К ОСВОЕНИЮ МАТЕРИАЛА Требования по разделу «Линейная алгебра» [1,2,3,4,8,9]

Необходимо уметь:

С1. Вычислять определитель второго порядка, третьего порядка

(«треугольниками» и разложением по произвольной строке или столбцу), четвертого высших порядков.

2. кладывать, перемножать, транспонировать матрицы. матриц3. Выч слять м норы квадратных матриц, находить алгебраиче-

ские дополнен я элементов квадратной матрицы. Вычислять миноры про звольного порядка.

4. Решать с стемы линейных уравнений методами Крамера, матричнымбА, Гаусса.

5. Решать матр чные уравнения.

6. Наход ть ранг матрицы по определению, методом окаймляющ х м норов.

7. Проверять совместность системы линейных уравнений на основании теоремы Кронекера–Капели.

Необходимо знать следующие темы:

1.Матрицы и действия с ними.

2.Определители, их свойства и вычисление.

3.Миноры, алгебраические дополнения.

4.Крамеровские системы линейных уравнений, их решение по формулам Крамера.

5.Крамеровские системы линейных уравнений, их решение матричным методом.

6.Решение матричных уравнений.

7.Решение систем линейных уравнений методом Гаусса.

8.Теорема Кронекера–Капелли. И

Требования по разделу «Векторная алгебра» [1,2,3,5,8,9]

Необходимо уметь:

1.Производить действия (складывать, вычитать, находить проекции и пр.) с геометрическими векторами.

2.Производить действия (складывать, вычитать, находить длину

ипр.) с векторами при известных координатах.

297

3.	Находить длину, орт, направляющие косинусы вектора.
4.	Вычислять скалярные, векторные, смешанные произведения
векторов.
5.	Находить углы между векторами.
6.	Находить расстояния между точками, площадь треугольника,
С
площадь параллелограмма, объем параллелепипеда, объем пирамиды,
высотутреугольника,высотупирамиды,решатьгеометрическиезадачи.
Необход мо знать следующие темы:
произведение
1.	Понят е вектора, арифметические операции с векторами, их
свойства.
2.	Проекц я вектора на ось, основная теорема о проекциях.
3.	Баз	с коорд наты вектора на плоскости и в пространстве,
	бА
действ я с векторами			координатной форме записи.
4.	Орт	коорд наты вектора.
5.	Скалярное			векторов, его основные свойства,
критер й перпенд кулярности, использование.
6.	Выч	слен е скалярного произведения через координаты век-
торов.
7.	Векторное произведение векторов, его основные свойства,
критерий коллинеарности, использование.
8.	Вычисление векторного произведения через координаты век-
торов.
9.	Смешанное произведение векторов, его геометрический
смысл, вычисление, использование.
10. Вычисление смешанного произведения через координаты
векторов.					И

	Требования по разделу «ДАналитическая геометрия»
			[1,2,3,4,6,8,9]

Необходимо уметь:

1.Находить расстояние между точками.

2.Проводить прямую через две точки, через точку параллельно (перпендикулярно, под углом) к данной прямой.

3.Вычислять угол между прямыми. Находить точку пересечения прямых, расстояние от точки до прямой.

4.Приводить к каноническому виду, строить эллипс, гиперболу, параболу.

298

5.	Проводить плоскость через три точки, через прямую и точку,
через две параллельные прямые.
6.	Находить расстояние от точки до плоскости, находить проек-
цию точки на плоскость.
7.	Находить прямую в пространстве, по двум точкам, угол меж-
ду прямыми в пространстве, приводить уравнение к каноническому
виду.
8.	Наход ть угол между прямой и плоскостью, точку пересече-
ния прямой		плоскости.
Необход мо знать следующие темы:
С
1.	Декартова прямоугольная система координат. Полярная сис-
тема коорд нат.
2.	Уравнен е прямой с угловым коэффициентом, угол между
	, услов е параллельности, перпендикулярности.
3.	Общее уравнен е прямой, уравнение прямой в отрезках, вза-
прямыми
имное положен е прямых на плоскости.
4.	Кр вые второго порядка: эллипс, гипербола, парабола.
5.	Общее уравнение плоскости, его частные виды, уравнение
плоскости в отрезках.
6.	Угол	между плоскостями, плоскость, проходящая через три
точки, расстояние от точки до плоскости.
7.	Уравнения прямой в пространстве: каноническое, параметри-
ческое, как пересечение двух плоскостей.
8.	бА
	Взаимное расположение прямых и плоскостей в пространстве.
9.	Поверхности второго порядка.
Требования по разделу «Введение в математический анализ»
		[1,2,3,7,8,9,10,11]Д
Необходимо уметь:			И

1.Вычислять пределы последовательностей.

2.Вычислять пределы функций в точке и на бесконечности, исследовать различные типы неопределенностей.

3.Использовать замечательные пределы, эквивалентности бесконечно малых.

4.Находить односторонние пределы.

5.Исследовать точки разрыва.

299

Необходимо знать следующие темы:

1.	Понятия функции, сложной функции.
2.	Предел числовой последовательности.
3.	Бесконечно малые последовательности, их связь с бесконечно
большими последовательностями.
С
4.	Основные свойства последовательностей, имеющих предел.
5.	Понятие предела функции в точке и на бесконечности.
6.	Основные свойства предела функции.
7.	Замечательные пределы.
Точки
8.		равнен е бесконечно малых функций, эквивалентные беско-
нечно малые функц , х использование.
9.	Непрерывность функции в точке, основные свойства непре-
рывных функц й.
10.		бА
		разрыва графика функции, их классификация.

Требован я по разделу «Дифференциальное исчисление функции одной действ тельной переменной» [1,3,7,8,9,10,11]

Необходимо уметь:

1.Вычислять производные функций, заданных явно, неявно, параметрически.

2.Вычислять дифференциалы.

3.Находить приближенное значение функции с помощью дифференциала.

4.Находить наибольшее и наименьшее значения функции на от-

резке.

5.Находить вертикальные, горизонтальные, наклонные асим-

птоты.

6.Находить промежутки монотонности функции, точки экстре-

мума.

7.Находить промежутки выпуклости, вогнутости, точки переги-

ба.

8.Находить область определения функции, исследовать на четность, нечетность, периодичность.

9.Проводить полное исследование функции с помощью производных, строить график.

10.Применять правило Лопиталя при вычислении производных.

11.Раскладывать функции по формулам Тейлора и Маклорена, выписывать виды остаточных членов. И

300

12. Вычислять приближенные значения функции и оценивать точность вычислений с помощью формулы Тейлора и остаточных членов.

Необходимо знать следующие темы:

1.	Определение производной. Геометрический смысл производ-
ной. Физический смысл производной.
2.	Вторая производная. Физический смысл второй производной.
3.	Уравнен е касательной. Уравнение нормали.
4.	Основные свойства производной. Производные элементарных
высших
функц й. Про зводная сложной функции. Производные от функций,
Сзаданных неявно. Про зводные от функций, заданных параметриче-
ски.
5.	Логар фм ческое дифференцирование.
6.	бА
	Про зводные		порядков.
7.	Д фференц ал функции. Геометрический смысл дифферен-
циала.	Формулы пр	л женных вычислений с помощью дифферен-
циала.	Д фференц алы высших порядков.
8.	Нахождение о ласти определения функции, проверка четно-
сти, нечетности, периодичности.
9.	Асимптоты функции: горизонтальные, вертикальные, наклон-
ные.
10. Исследование функции с помощью первой производной.
			Д
Промежутки монотонности, экстремумы.
11. Исследование функции с помощью второй производной.
Промежутки выпуклости, вогнутости, точки перегиба.
12. Нахождение эктремумов функции с помощью второй произ-
			И

водной.

13. Наименьшее и наибольшее значения функции на отрезке.

14. Правило Лопиталя.

15. Формулы Тейлора и Маклорена.

16. Форма Лагранжа, форма Коши остаточного члена формулы Тейлора.

301

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3031 / 3131

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20214.82 Mб102270.pdf
#
07.01.20214.82 Mб412271.pdf
#
07.01.20214.82 Mб52272.pdf
#
07.01.20214.85 Mб32273.pdf
#
07.01.20214.86 Mб392276.pdf
#
07.01.20214.86 Mб102277.pdf
#
07.01.20214.86 Mб422278.pdf
#
07.01.20214.88 Mб392279.pdf
#
07.01.2021360.3 Кб9228.pdf
#
07.01.20214.88 Mб972280.pdf
#
07.01.20214.89 Mб132281.pdf