Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Сибирская государственная автомобильно-дорожная академия
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
2277.pdf
Скачиваний:
10
Добавлен:
07.01.2021
Размер:
4.86 Mб
Скачать
☆
►Содержание►

36.

Определите неопределенное выражение, возникающее при

вычислении пределов.

 

 

37.

Какие типы неопределенностей вы знаете?

38.

Какие пределы называют первым замечательным пределом?

вторым замечательным пределом?

С

 

 

39.

Дайте определение эквивалентных б.м.

40.

формулируйте теорему о вычислении пределов с помощью

эквивалентностей б.м.

 

 

41.

Нап ш те основные эквивалентности б.м.

определение

 

42.

Что называют

приращением аргумента и приращением

функц

?

 

 

43.

Пр вед те

 

функции, непрерывной в точке.

44.

В каком случае функция является непрерывной на отрезке?

45.

бА

Как е точки называют точками разрыва функции?

46.

Дайте

устранимого разрыва функции.

47.

Какая точка разрыва является точкой разрыва первого рода?

48.

В как х случаях функция имеет разрыв второго рода?

49.

Сформул руйте терему Вейерштрасса и ее следствие.

50.

Сформулируйте терему Коши и ее следствие.

Раздел 4. ДИФФЕРЕНЦИ ЛЬНОЕ ИСЧИСЛЕНИЕ

 

 

 

Д

ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ

ПЕРЕМЕННОЙ

 

 

4.1. ПРОИЗВОДНАЯ ФУНКЦИИ. ОСНОВНЫЕ ПРАВ ЛА

ДИФФЕРЕНЦИРОВАНИЯ

И

 

§ 34. Определение производной функции

Производной функции f (x) в точке x0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (прил. 28).

Производная обозначается f (x0).

Пусть функция y = f (x) определена в точке x0 и некоторой ее окрестности, x – точка из этой окрестности. Введем обозначения: разность x – x0 обозначим через x и назовем приращением аргумента,

161

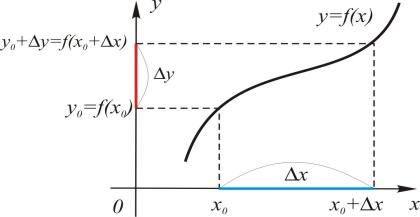
разность f(x) – f(x0) обозначим через y и назовем приращением функции (рис. 92).

С

 

 

 

 

 

 

 

 

 

 

 

 

 

обозначен

 

 

 

 

 

 

 

иРис. 92

 

 

 

 

 

 

 

Введем

 

 

 

А

 

 

 

 

 

 

 

я: x= x – x0; y= f(x) – f(x0). Отсюда полу-

чаем равенства

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x = x0 + x, тогда

y= f(x0 + x) – f(x0).

 

 

Итак,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f (x 0) lim

 

y

 

lim

f (x0

x) f (x0 )

lim

 

f (x) f (x0)

.

 

 

 

 

 

 

 

 

 

 

x 0 x

x 0

 

x

 

x x0

x x

0

 

Пример

 

 

 

 

 

 

 

 

 

 

И

 

 

 

 

 

 

 

Д

Найти производную для функции f (x) = x 2 в точке x0 = 3.

 

 

 

f (3 x) f (3)

(3 x)2 32

 

 

 

 

 

 

 

 

 

 

lim

 

 

 

 

 

 

 

f (3) lim

x

 

 

x

 

 

 

x

0

 

x 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

lim

9 6 x ( x)2 9

lim

6 x ( x)2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

x 0

 

 

 

x 0

x

 

 

 

lim (6 x) 6.

x 0

162

Если производная f (x0) существует, то говорят, что функция f (x) дифференцируема в точке x0. Установим связь между дифференцируемостью функции f (x) в точке x0 и ее непрерывностью в этой точке. Напомним, что функция f (x) непрерывна в точке x0, если она определена в точке x0 и некоторой ее окрестности, и выполняется равенство

lim f (x) f (x0).

x x0

 

Переформул руем определение, используя понятия приращения

и

 

аргумента пр ращен я функции. Из приведенного равенства полу-

Счаем

 

бА

lim ( f (x) f (x0)) 0;

lim ( f (x0 x) f (x0)) 0;

x x0

x 0

lim y 0.

x 0

Другими словами, функция f (x) непрерывна в точке x0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

 

Д

Теорема. Если функция f(x) дифференцируема в точке x0, то она

непрерывна в этой точке.

 

Замечание. Если в точке x0 функция f (x) непрерывна, то в этой

точке функция может и не иметь производной, что подтверждается

следующим примером.

 

 

 

И

Пример

 

 

 

 

 

 

непрерывна в точке x0=0, так как

Функция f (x)

 

x

 

 

 

lim

x

 

0

0

.

 

 

 

 

 

x 0

 

 

 

 

 

 

 

 

 

 

Покажем, что эта функция не имеет производной в точке x0:

 

 

 

f

 

y

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

lim

, но

 

 

(0) lim

 

 

 

 

 

x 0 x

x 0 x

 

163

 

x

 

1,

если x 0;

поэтому lim

 

 

x

 

 

1,

 

 

 

 

1,

если x 0,

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

x 0 0 x

 

 

 

а lim

 

x

1, значит, lim

 

x

 

не существует, т.е. f (x) не диффе-

 

 

 

 

 

 

 

 

 

 

 

x 0 0 x

 

 

 

 

 

 

 

x 0 x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ренцируема в точке x0 = 0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

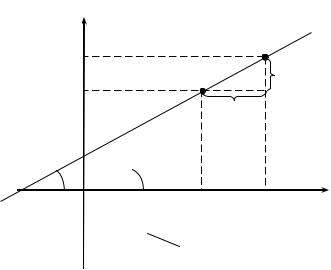
Геометрический смысл производной

геометрический

смысл производной.

Рассмотр м

 

 

 

 

 

СНа р с. 93 зо ражен график непрерывной функции y = f (x).

 

 

б

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f (x0 x)

 

 

 

 

 

 

 

 

 

 

 

 

M

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

f (x0)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A

 

 

 

 

 

 

 

 

 

 

 

А

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

K

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x0 x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y = f(x)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 93

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Точка M0 на графике имеетДкоординаты (x0, f (x0)), еще одна

точка графика M – координаты

(x0 +

x,

f(x0

+ x)). Прямая M0M

является секущей для линии y = f(x),

она наклонена к оси Ox под уг-

лом .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

И

Пусть

f

 

(x0) существует, т. е.

lim

 

y

 

 

 

 

 

 

 

 

 

–

некоторое число. з

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

x 0 x

 

 

 

 

 

M0MА получаем, что

tg

(известно, что tg – угловой коэф-

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

фициент прямой M0M). Если x 0, то точка M движется по графику функции y = f (x), приближаясь к точке M0, при этом секущая

164

M0M, поворачиваясь вокруг точки M0, стремится занять предельное положение, т. е. совпасть с касательной M0K, при этом ( – угол между касательной M0K и осью Ox); tg = tg .

Таким образом,

f (x0) lim

y

tg ,

но tg = k есть угловой

 

С

 

x 0

x

 

коэффициент касательной M0K.

 

 

 

 

Итак, угловой коэффициент касательной к графику y = f (x) в

точке с абсц ссой x0 равен производной функции f (x) в точке x0:

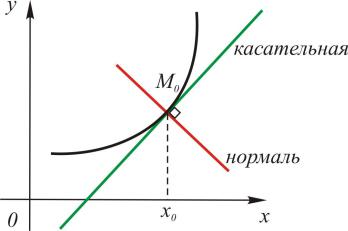
уравнение

 

 

 

 

 

 

 

f (x0) = k = tg .

 

В этом состо т геометрический смысл производной.

бА

Очев дно, что

 

касательной (рис. 94) имеет вид

 

y – f (x0) = f (x0)(x – x0).

 

 

Д

 

 

Рис. 94

И

 

 

 

Уравнение нормали (см. рис. 94) имеет вид

 

y – f (x0) =

 

1

(x – x0).

 

 

 

 

 

 

f (x0 )

 

Переходим к рассмотрению механического смысла производ-

ной.

165

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности