
- •Введение
- •Раздел 1. ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА
- •1.1. ЛИНЕЙНАЯ АЛГЕБРА
- •§1. Матрицы и действия с ними
- •§2. Определители
- •§3. Обратная матрица
- •§4. Крамеровские системы линейных уравнений. Метод Крамера
- •§5. Крамеровские системы линейных уравнений. Матричный метод решения систем линейных уравнений
- •§6. Ранг матрицы
- •§7. Системы линейных уравнений: общий случай
- •§8. Метод Гаусса
- •§9. Однородные системы
- •1.2. ВЕКТОРНАЯ АЛГЕБРА
- •§12. Базис и координаты
- •§13. Орт и направляющие косинусы
- •§15. Векторное произведение векторов
- •§16. Смешанное произведение векторов
- •§17. Основные понятия
- •§18. Полярная система координат
- •§19. Прямая на плоскости
- •§20. Кривые второго порядка. Эллипс
- •§21. Гипербола
- •§22. Парабола
- •§23. Плоскость
- •§24. Прямая в пространстве
- •§25. Поверхности второго порядка
- •Раздел 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •3.2. ТЕОРИЯ ПРЕДЕЛОВ
- •§ 29. Предел функции
- •§ 30. Основные свойства пределов функции
- •§ 31. Замечательные пределы
- •3.3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- •§ 32. Непрерывность функции в точке
- •§ 33. Точки разрыва графика функции и их классификация
- •§ 34. Определение производной функции
- •§ 35. Производные некоторых элементарных функций
- •§ 36. Основные правила дифференцирования
- •§ 39. Дифференциал функции
- •§ 40. Производные и дифференциалы высших порядков
- •§ 41. Правило Лопиталя
- •§ 43. Нахождение наибольшего и наименьшего значений функции на отрезке
- •§ 44. Схема исследования функции и построения графика
- •§ 45. Формула Тейлора
- •Задачи для самостоятельного решения
- •Библиографический список
5. Вычислить площадь параллелограмма, построенного на век-
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1; |
|
|
|
|
|
30 . |
||||||||||||||||||||||||||||||||||||||||
торах |
3 |
b |
|
и 3 |
|
b |
, если |
|
a |
|
|
|
|
|
b |
|
|
a |
, |
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
a |
|
3 |
|
3 |
a |
|
|
|
|
|
|
|
|
|
3 |
|
a |
|
|
a |
|
|
a |
|
|
|
|
9 |
|
|
a |
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
|
b |
b |
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Используем свойства векторного произведения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
a |
0; b b 0; |
a |
b b |
a |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 0 |
a |
|
|
|
|
|
9 |
a |
|
|
|
3 0 8 |
a |
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Далее |
b |
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Sпар |
|
8 |
a |
|
|
|
|
|
8 |
|
|
a |
|
|
|
|
|
|
8 |
|
|
a |
|
|
|
|
|
|
|
|
|
sin 8 1 1 sin30 8 |
1 |
4 кв.ед. . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
b |
|
|
|
b |
|
|
|
|
|
|
|
b |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
и6. Дана с ла F 5, 1, 4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
точки A 2,3,6 и B 1,5, 3 . Оп- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ределить момент с лы F относительно точки В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Момент силы F , приложенной к точке |
|
|
относительно точ- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ки В, – это вектор, равный векторному произведению вектора пере- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
мещения |
|
3; 2;9 на вектор силы F : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
BA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
|
|
|
|
|
|
|
|
|
А3 2 9 = 17i 57 j 7k. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BA |
F |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
Итак, найден искомый момент силы |
|
|
|
|
|
|
17i 57 j 7k. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
F0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
§16. Смешанное произведение векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Тройка некомпланарных векторов |
a |
, |
|
|
, |
c |
|
называется правой, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
если векторы |
a |
|
|
и |
c |
|
|
расположены по одну и ту же сторону плос- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
кости, проведённой через |
a |
и |
|
|
(рис. 15). |
|
|
|
|
И |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Замечание. Если |
a |
, |
|
b |
|
, |
c |
|
|
|
|
правая тройка, |
то |
b |
, |
с |
, |
a |
и |
c |
, |
a |
, |
b |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тоже правые, а тройки |
|
, |
a |
, |
c |
; |
|
|
|
a |
, |
c |
, |
|
; |
c |
, |
|
, |
a |
левые. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
59
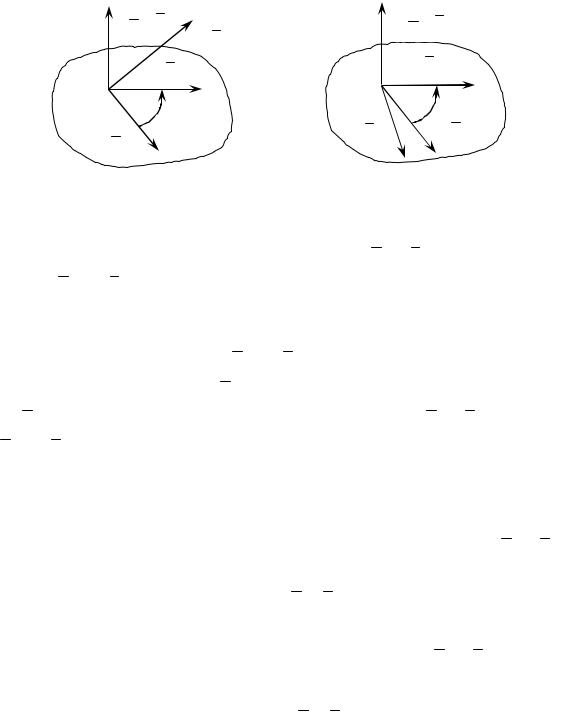
a b |
с |
Правая |
a b |
Левая |
|
тройка |
b |
тройка |
|
|
b |
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
||||||||||||||||
геометрический |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
мешанным про зведением векторов |
a |
, |
b |
, |
c |
называется число, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
равное |
a |
|
b |
|
c |
(см. пр л. 11). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
Теорема ( |
|
|
|
|
|
|
|
|
смысл смешанного произведения). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Смешанное про зведение |
a |
|
b |
|
c |
|
|
равно объёму параллелепипеда, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
построенного на векторах |
a |
, |
b |
,c , взятого со знаком плюс, если трой- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ка |
a |
,b,c правая, и со знаком минус, если |
a |
,b, |
c |
левая. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
c |
V . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b |
Основное использование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1. Объём параллелепипеда, построенного на векторах |
a |
,b, |
c |
: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vпар |
|
|
a |
|
|
|
|
c |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||||||||||
|
|
|
|
|
2. Объём пирамиды, построенной на векторах |
a |
,b, |
c |
: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
1 |
|
a |
b |
c |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пир |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Теорема (выражение смешанного произведения векторов через их координаты). Смешанное произведение имеет вид
60

|
|
|
|
xa |
ya |
za |
|
a |
b |
c |
|
xb |
yb |
zb |
, |
|
|
|
|
xc |
yc |
zc |
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
b xb, |
|
|
|
|
|
|
, zb ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
где |
a |
xa , |
ya, za ; |
yb |
|
c |
|
xc , |
|
|
yc, zc |
|
|
|
координаты |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
векторов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Доказательство. По определению, |
|
a |
|
|
|
|
|
|
c |
|
a |
( |
|
|
|
|
|
c |
). |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
b |
b |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yb |
|
zb |
|
|
|
|
|
|
|
|
|
|
xb |
|
|
|
zb |
|
|
|
|
|
|
|
|
|
|
|
xb |
yb |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
По теореме § 15, |
|
|
|
b c i |
|
|
j |
|
|
|
k |
. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
yc |
|
zc |
|
|
|
|
xc |
|
|
|
zc |
|
|
|
xc |
yc |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
бА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
По теореме § 14, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xa |
|
|
|
|
|
|
ya |
|
za |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
b |
|
c |
xa |
|
yb |
|
zb |
|
ya |
|
xb |
|
|
|
zb |
|
|
za |
xb |
yb |
|
|
xb |
|
|
|
|
|
|
yb |
|
zb |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yc |
|
zc |
|
|
|
|
|
|
|
xc |
|
|
|
zc |
|
|
|
|
|
|
|
|
|
xc |
yc |
|
|
|
|
|
|
xc |
|
|
|
|
|
|
yc |
|
zc |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Критерий компланарности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
,b, |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Векторы |
|
компланарны тогда и только тогда, когда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
c 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1. Найти смешанное произведение векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i |
j k; b i 3 j k ; |
с |
i j 4k . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||||||||||||||||||||||
|
|
2 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
a |
bc |
|
|
1 3 |
1 |
|
2 |
|
1 |
|
|
1 |
|
|
|
26 5 2 33. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
4 |
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2. Показать, что векторы |
|
|
|
a |
|
5 |
|
7 |
|
; |
|
|
|
|
|
|
|
; |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j |
k |
b |
j |
k |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2i |
i |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
61

с i 2 j 2k компланарны.
Решение. Находим смешанное произведение векторов:
|
2 |
5 |
|
7 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a |
bc |
|
1 |
1 |
|
1 |
2 |
5 |
7 |
8 15 7 0. |
||||||||||
|
|
2 |
2 |
1 |
2 |
1 |
2 |
||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Так как |
a |
|
|
|
|
|
||||||||||||||
|
|
bc |
0, то векторы компланарны. |
|
|
||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3. Найти о ъём треугольной пирамиды с вершинами A 2,2,2 ; |
||||||||||||||||||||
B 4,3,3 ; C 4,5,4 ; D 5,5,6 . |
|
|
|
|
|
|
|
||||||||||||||
Решен е. Найдём векторы AB, AC, AD, совпадающие с ребрами пи-
|
|
|
|
|
|
(все векторы должны исходить из одной точки). |
|||||||||||||||||||||||||||||||||
рамиды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
AB 2,1,1 a; |
AC 2,3, 2 |
|
; |
|
|
|
3,3, 4 |
c |
. |
||||||||||||||||||||||||
b |
|
AD |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
б |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Так как Vпир |
|
|
a bc , найдём смешанное произведение |
|||||||||||||||||||||||||||||||||
6 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
1 |
1 |
|
|
|
|
3 |
|
2 |
|
|
2 |
2 |
|
|
|
2 |
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|||||||||||||||||||||||
a bc |
|
2 3 |
2 |
|
2 |
2 6 1 2 1 3 7. |
|||||||||||||||||||||||||||||||||
|
|
|
4 |
1 |
3 |
4 |
1 |
3 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
3 |
4 |
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ед.3 |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
1 |
7 |
7 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пир |
6 |
Д |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||||
4. Вычислить a b b c c a . И
Решение. Так как a b b c c a 0, то эти векторы компланарны. Следовательно, их смешанное произведение равно нулю:
a b b c c a 0.
62

|
Вопросы и задания для самопроверки по теме |
|
«Векторная алгебра» ([1,2,3,5,8,9], прил. 8 11) |
1. |
Что называется геометрическим вектором? |
2. |
Что называется длиной геометрического вектора? |
С |
|
3. |
Какие векторы называются одинаково направленными? |
4. |
Какие векторы называются коллинеарными? |
5. |
Дайте определение сложения двух геометрических векторов. |
6. |
Определ те умножение геометрического вектора на число. |
координаты |
|
7. |
Что называется проекцией вектора на ось? |
8. |
Какая с стема векторов называется линейно независимой? |
9. |
Как е векторы называются компланарными? |
10. Что такое аз с плоскости и в пространстве?
13.СформулбАруйте критерий линейной зависимости системы
векторов.
14.Каково наи ольшее количество линейно независимых векторов на плоскости?
15.Каково наи ольшее количество линейно независимых векторов в трехмерном пространстве?
16.Что называется координатамиДвектора в декартовой прямоугольной системе координат (ДПСК)?
17.Сформулируйте теорему о разложении вектора по ортам координатных осей.
18.Дайте определение направляющих косинусов вектора.
19.Какое основное свойство направляющихИкосинусов вектора?
20.Сформулируйте условие коллинеарности векторов.
21.Определите скалярное произведение векторов.
22.Как выглядит критерий перпендикулярности векторов?
23.Напишите формулу для вычисления через координаты скалярного произведения векторов.
24.Каков геометрический смысл скалярного произведения?
25.Чему равно скалярное произведение j k ?
26.Что называется скалярным произведением n-мерных векто-
ров?
27.Дайте определение векторного произведения векторов.
28.Сформулируйте критерий коллинеарности векторов.
63

29. |
Как вычисляют через координаты векторов их векторное |
||||
произведение? |
|||||
30. Поясните геометрический смысл векторного произведения. |
|||||
31. |
|
|
|
|
|
Чему равно векторное произведение i |
j? |
||||
32. |
Какие векторы называются компланарными? |
||||
С |
|||||
33. |
Какая упорядоченная тройка векторов называется правой? |
||||
34. |
Определите смешанное произведения векторов. |
||||
35. Как выч сляется смешанное произведение через координаты векторов-сомнож телей?
|
|
терий |
|||||||||||||||
36. |
Каков геометр ческий смысл смешанного произведения век- |
||||||||||||||||
торов? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
37. Зап ш те кр |
компланарности трех векторов. |
||||||||||||
38. |
Чему равно смешанное произведение базисных векторов |
||||||||||||||||
|
|
|
|
|
|
бА |
|||||||||||
i, j, k ? |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
39. |
Чему равно векторное произведение двух коллинеарных век- |
||||||||||||||||
торов? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
40. |
Чему равно скалярное произведение двух коллинеарных век- |
||||||||||||||||
торов? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Экспресс-тест по теме «Векторная алгебра» |
|||||||||||
1. |
Является ли вектором сумма двух векторов? |
||||||||||||||||
2. |
Равна ли 1 длина вектора |
a |
(1; 2; 2)? |
||||||||||||||
3. |
Разложение вектора |
|
a |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
(1; 2; 2) в базисе i |
; j;k равно |
|||||||||||||||
i2j 2 k ?
4.Образуют ли векторы a (1; 2) и b ( 2;4) базис на плос-
кости?
5.Верно ли, что a b b ?
6.Коллинеарны ли векторы a b и b a?
7.Могут ли направляющие косинусы вектора иметь значенияДИ
cos |
1 |
; cos |
1 |
; cos |
|
1 |
? |
|
|
2 |
|||||
2 |
2 |
|
|
|
|||
8.Является ли вектором векторное произведение векторов?
9.Смешанноепроизведениетрехкомпланарныхвекторовравно1?
10.Смешанноепроизведениетрехколлинеарныхвекторовравно0?
11.Является ли правой тройка векторов k, i, j?
64
