
- •Введение
- •Раздел 1. ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА
- •1.1. ЛИНЕЙНАЯ АЛГЕБРА
- •§1. Матрицы и действия с ними
- •§2. Определители
- •§3. Обратная матрица
- •§4. Крамеровские системы линейных уравнений. Метод Крамера
- •§5. Крамеровские системы линейных уравнений. Матричный метод решения систем линейных уравнений
- •§6. Ранг матрицы
- •§7. Системы линейных уравнений: общий случай
- •§8. Метод Гаусса
- •§9. Однородные системы
- •1.2. ВЕКТОРНАЯ АЛГЕБРА
- •§12. Базис и координаты
- •§13. Орт и направляющие косинусы
- •§15. Векторное произведение векторов
- •§16. Смешанное произведение векторов
- •§17. Основные понятия
- •§18. Полярная система координат
- •§19. Прямая на плоскости
- •§20. Кривые второго порядка. Эллипс
- •§21. Гипербола
- •§22. Парабола
- •§23. Плоскость
- •§24. Прямая в пространстве
- •§25. Поверхности второго порядка
- •Раздел 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •3.2. ТЕОРИЯ ПРЕДЕЛОВ
- •§ 29. Предел функции
- •§ 30. Основные свойства пределов функции
- •§ 31. Замечательные пределы
- •3.3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- •§ 32. Непрерывность функции в точке
- •§ 33. Точки разрыва графика функции и их классификация
- •§ 34. Определение производной функции
- •§ 35. Производные некоторых элементарных функций
- •§ 36. Основные правила дифференцирования
- •§ 39. Дифференциал функции
- •§ 40. Производные и дифференциалы высших порядков
- •§ 41. Правило Лопиталя
- •§ 43. Нахождение наибольшего и наименьшего значений функции на отрезке
- •§ 44. Схема исследования функции и построения графика
- •§ 45. Формула Тейлора
- •Задачи для самостоятельного решения
- •Библиографический список
38. Приведите к каноническому виду, назовите и постройте поверхность x2 4y2 8z2 6x 10y 4z 5 0.
39. Цилиндрические поверхности, их определение и свойства. 40. Приведите к каноническому виду, назовите и постройте по-
верхность x2 4y2 6x 10y 5 0.
Сских3.1. ОСНОВНЫЕ ПОНЯТИЯ ФУНКЦИИ ОДНОЙ
Раздел 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ПЕРЕМЕННОЙ
§ 26. Математ ческие символы. Множества
ЗачаткиАбелемметодов математического анализа были у древнегречематемат ков (Архимед). Систематическое развитие эти методы получ ли в XVII в. в трудах Ньютона и Лейбница. В XVIII XIX вв. фактическ й матер ал ыл логически обобщен Эйлером, Коши, Ло-
бачевским, , Риманом и другими учеными. Дифференциальное исчисление раздел математического ана-
лиза, в котором изучаются понятия производной, дифференциала и |
||
способы их применения к исследованию функций. Математический |
||
|
Д |
|
анализ изучает количественные соотношения действительного мира. |
||
В анализе преимущественноАрассматриваются переменные величины, |
||
характеризующие процессы, зависимость между ними описывается с |
||
помощью функций. |
|
|
Формирование дифференциального исчисления связано с име- |
||
|
Именно |
|
нами Исаака Ньютона и Готфрида Лейбница. |
они четко |
|
сформулировали основные положения математического анализа и указали на взаимообратный характер дифференцирования и интегрирования. Создание дифференциального исчисления (вместе с интегральным) открыло новую эпоху в развитии математики. С этим связаны такие дисциплины, как теория рядов, теория дифференциальных уравнений и многие другие. Методы математического анализа нашли применение во всех разделах математики. Очень распространилась область применения математики в естественных науках и технике.
Дифференциальное исчисление базируется на важнейших понятиях математики, определение и исследование которых и составляют предмет введения в математический анализ: действительные числа
118
(числовая прямая), функция, граница, непрерывность. Все эти понятия получили современную трактовку в ходе развития и обоснования дифференциального и интегрального исчислений.
Основная идея дифференциального исчисления состоит в изуче- |
|
нии функции в малом. Точнее, дифференциальное исчисление дает |
|
С |
|
аппарат для исследования функций, поведение которых в достаточно |
|
малой окрестности каждой точки близко к поведению линейной |
|
функц |
ли многочлена. Таким аппаратом служат центральные по- |
нятия д фференц ального исчисления: производная и дифференциал. Оф ц альной датой рождения дифференциального исчисления можно сч тать май 1684 г., когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…». Эта статья в сжатой малодоступной форме излагала принципы нового метода, названно-
дав тем самымЛейбницаи одно из названий новому разделу математики. В ос-
го дифференц альным |
счислением. |
|
В конце XVII в. |
вокруг |
возникает кружок, видней- |
представ телями которого |
ыли братья Якоб и Иоганн Бернул- |
|
шими |
|
|
ли и Лоп таль. В 1696 |
г., используя лекции И. Бернулли, Лопиталь |
|
написал первый уче н к, излагавший новый метод в применении к
теории плоских кривых. Он назвал его « нализ бесконечно малых»,
нову изложения положено понятие переменных величин, между которыми имеется некоторая связь, из-за которой изменение одной влечёт изменение другой.
А В математике употребляютсяДспециальные символы, позволяю-
щие сократить запись и точнее выразить утверждение:
, , , , , 
 , , , , (прил. 21) .
, , , , (прил. 21) .
Например, применяя символ «>» к числам a, b, получим запись «a > b», которая является сокращением для предложения «Число a больше числа b». Если l1, l2 – обозначения прямых, то запись l1 || l2 есть утверждение, что l1 параллельна l2 . Запись «x M» означает, что x является элементом множества M.
Логические символы: |
|
|
, &, , , , , . |
|||
1.Отрицание применяется к одному высказываниюИили преди- |
||||||
кату, соответствует частице «не» и обозначается |
A |
(или A). |
||||
Например, формула |
|
есть сокращение для предложения |
||||
3 0 |
||||||
«–3 не больше 0» («неверно, что –3 больше 0»).
2.Конъюнкция применяется к двум высказываниям или предикатам, соответствует союзу «и», обозначается А & B (или A B).
119
Так, формула (–3 > 0) & (2 2 = 4) означает предложение «–3 > 0 и 2 2 = 4», которое, очевидно, ложно.
3.Дизъюнкция применяется к двум высказываниям или предикатам, соответствует союзу «или» (неразделительному) и обозначается
A B . |
|
С |
или множе- |
Предложение «Число x принадлежит множеству M1 |
ству M2» изображается формулой x M1 x M2 .
4.Импл кац я соответствует союзу «если ..., то ...» и обозначается A B.
Так,зап сь«a > –1 a > 0»естьсокращениедляпредложения «Ес-
лиa>–1,тоa>0».
5. |
Экв валенц я A B соответствует предложению «A тогда и |
только тогда, когда B». |
|
6. |
Квантор о щности читается, как «любой», «каждый», |
«все» |
с предлогом «для»: «для любого», «для всех» и так далее. |
Кванторлипр меняется к предикату F(x, ...), содержащему одну пе- |
|
ся» и аналогичнобА. Квантор , примененный к предикату F(x,...), соответствует предложению «СуществуетДx, такой, что F(x,...)» («Найдется x, для которого F(x,...)») и обозначается x F(x,...).
ременную (напр мер, x) или несколько переменных, при этом получа-
ется формула x F(x,...), |
которая соответствует предложению «Для |
любого x выполняется |
F(x, ...)» или «Все x обладают свойством |
F(x, ...)». |
|
7. Квантор существования читается «существует», «найдет- |
|
Понятие множества является первоначальным понятием математики, точное определение множества не дается, но его можно пояснить, описать через другие понятия. Можно сказать, что множество – это совокупность, собрание каких-то объектовИ, предметов, при этом объект, входящий в это множество, называют его элементом. Множества могут содержать как конечное число элементов, так и бесконечно много элементов. Рассматривают и множество, не содержащее элементов,егоназываютпустым, обозначают символомØ.
В математическом анализе чаще всего рассматриваются числовые множества, за некоторыми из них закреплены специальные обозначения.
Множество всех натуральных чисел: N = {1,2,3,...}.
Множество всех целых чисел Z содержит натуральные числа,
ноль, целые отрицательные числа: Z = {..., –3, –2, –1, 0, 1, 2, 3, ...}.
120
Множество рациональных чисел обозначается через Q. Рацио-
нальным называется число, которое можно представить в виде отно-
шения двух целых чисел: |
|
p |
(p Z, |
q Z, q 0), т. е. |
||||
|
q |
|||||||
С |
|
|
|
|
|
|||
def |
|
p |
|
|
||||
Q |
{ |
|
|
|
| p Z & q Z & q 0}. |
|||
def |
q |
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
Здесь знак заменяет слово «называется» или «равно по опре- |
||||||||
делению». Известно, что любое рациональное число можно представить десят чной дробью, конечной и бесконечной периодической. Например, рац ональное число 5/6 представимо бесконечной перио-
дробью 5/6 = 0,83333..., а число 3/8 = 0,375. В последнем случае можно сч тать десятичную дробь тоже бесконечной с числом 0 в пер оде: 3/8 = 0,3750000... . Известно, что всякую периодическую
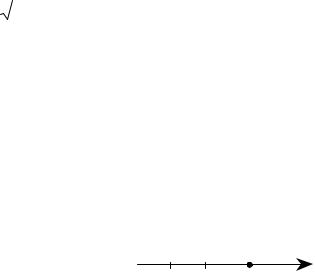
x будет соответствовать определенная точка М, абсцисса которой равна x. Такая прямая называется числовой осью (рис. 61).
бесконечную дро ь можно о ратить в обыкновенную дробь p/q. |
|||||
дической |
|
|
|||
Множество действительных чисел R – это множество всех бес- |
|||||
конечных десят чных дро ей. Иррациональным числом называется |
|||||
всякая |
|
|
непериодическая десятичная дробь, т. е. множест- |
||
во всех рациональных и иррациональных чисел образует множество |
|||||
|
бесконечная |
|
|||
действительных чисел R. |
|
|
|||
Множество действительных чисел является подмножеством |
|||||
множества комплексных чисел C , т. е. чисел вида ai + b, где a R; |
|||||
b R; i |
1. |
А |
|||
|
|
|
|||
Из определения числовых множеств можно заключить, что |
|||||
|
|
|
N |
Z Q R C. |
|
На прямой выберем начало координат 0, единицу масштаба и |
|||||
|
|
|
|
Д |
|
положительное направление. Тогда каждому действительному числу |
|||||
|
|
|
|
М |
xИ |
0 1 x
Рис. 61
121

Промежутком называется совокупность чисел, заключенных между аи b.
В зависимости от того, присоединены концы промежутка к нему или нет, различают
– интервалы:
|
a,b x |
|
a x b ; |
|
|||||||||
|
|
|
|||||||||||
|
, a x |
|
|
|
x a ; |
|
|||||||
|
|
|
|||||||||||
|
, R вся числовая ось; |
||||||||||||
С– : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a,b x |
|
|
a x b ; |
|
||||||||
|
– полу нтервалы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
a,b x |
|
|
a x b ; |
|
||||||||
|
|
|
|||||||||||
отрезки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, x |
|
x a . |
интервал a,b , со- |
|||||||||
|
|
||||||||||||
|
Окрестностью точки x0 называется любой |
||||||||||||
держащий эту точку (рис. 62). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
x |
|
|||||||||
|
бА |
||||||||||||
|
( |
|
|
|
|
|
|
|
|
|
|
) |
|
|
a |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
Рис. 62 |
|
|
|||||||||
|
-окрестностью точки |
Д |
|||||||||||
x0 |
|
|
|
|
x0 |
называется |
интервал вида |
||||||
,x0 , 0 (рис. 63). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
x |
|
|||||||||
|
x0 |
|
|
|
|
|
|
|
|
|
x0 |
И |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 63
122

Точки x этого интервала удовлетворяют неравенствам
|
|
|
|
x0 x x0 ; |
||||||
|
|
|
|
x x0 ; |
||||||
§ 27. Функц |
|
|
x x0 |
|
. |
|||||
|
|
|||||||||
|
|
|
|
|
|
|||||
С |
|
|
|
|
|
|
||||
Пусть X |
|
Y ч словые множества. Функцией из множества X во |
||||||||
множество Y называется правило, по которому каждому числу x из |
||||||||||
множества X однозначно соответствует некоторое число y из множе- |
||||||||||
ства Y. Множество X называется областью определения функции, |
||||||||||
множествоиY называется о ластью значений. |
||||||||||
Обозначен я: |
|
|
|
|
|
|
||||
|
|
|
|
f : X Y ; |
|
|
X |
f |
||
|
|
|
|
|
|
Y; y f x . |
||||
Примеры: |
|
|
|
y x2 1. Тогда X , ее об- |
||||||
1. Рассмотрим функцию |
|
|
||||||||
ластьопределения; Y 1, областьзначений. |
||||||||||
бА |
||||||||||
2. Для функции y = |
|
|
x2 |
1 областью определения является |
||||||
множество X ; 1 & 1; ,множество значений Y 0, . |
||||||||||
|
|
|
2 |
x, если x 0; |
|
|
|
|||
sin |
|
здесь X = R, Y ; 1 . |
||||||||
3. y = |
1 |
|
|
|
|
|
|
|||
|
|
, если x 0, |
|
|
|
Д |
||||
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
Способы задания функцииИ
Основными способами задания функции одной переменной являются:
Аналитический способ: связь между аргументом x и функцией y задается формулой, при этом на разных участках области определения она может задаваться различными формулами (см. пример 2) . В примерах 1, 2 функции заданы аналитически.
123
Табличный способ: функция задается таблицей отдельных значений аргумента и соответствующих значений функции. Например, таблицы тригонометрических функций, таблицы логарифмов и так далее.
Графический способ: в этом случае соответствие между значе-
ниями x и y задается с помощью графика (прил. 23). |
|
|
|||||||
|
|
|
|
|
|
Элементарные функции |
|
|
|
1. |
y xn степенная функция. |
|
|
||||||
2. |
y ax a 0 показательная функция. |
|
|
||||||
С |
|
|
|
|
|
||||
3. |
y loga x логарифмическая a 0; a 1 . |
|
|
||||||
4. |
y sin x; |
|
|
|
|
||||
5. |
|
|
|
|
|
|
|
|
|
y cosx; |
тр гонометрические функции. |
|
|
||||||
|
|
|
|
|
|
|
|
||
и |
|
|
|||||||
6. |
y tgx; |
|
|
|
|
|
|||
7. |
y ctgx. |
|
|
|
|
|
|||
|
|
|
|
|
|
||||
8. |
y arcsinx; |
|
|
|
|||||
9. |
|
|
|
|
|
|
|
|
|
y arccosx; |
о ратные тригонометрические функции. |
|
|||||||
|
|
|
|
|
|
|
|
||
10. |
y arctg x; |
|
|
|
|||||
11. |
y arcctg x. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
бА |
|
|
||||||
|
|
|
|
|
|
Операции над функциями |
|
|
|
Функции можно складывать, вычитать, перемножать, делить. |
|
||||||||
Примеры: |
|
|
Д |
|
|||||
|
|
|
|
|
|||||
1. |
y |
2x2 sin x |
функция образована умножением функций |
||||||
y 2x2 |
и y |
2 |
sin x . |
|
|
|
|||
1 |
|
x2 |
|
|
|
|
|
||
2. |
y |
|
функция получена делением функций |
y x2 |
и |
||||
|
|
|
|||||||
y2 cosx. |
cosx |
|
|
И1 |
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
f |
|
Пусть даны две функции y x и z f y : X Y Z .
124

Сложной функцией z F x называется функция, имеющая об-
ластью определения X и областью значений Z, вычисляемая по прави-
лу z f x .
Примеры сложных функций:
1. z sin x2 y x2; |
z sin y . |
|
|
|
|
|
||||
С |
y sin x; z y2 . |
|
|
|
|
|
||||
2. z |
sin x 2 |
|
|
|
|
|
||||
3. u tg log2 x3 y x3; |
z log2 y; |
u tgz . |
||||||||
и |
|
|
|
|
|
|
||||
§ 28. Ч словые последовательности |
|
|
||||||||
Ч словой последовательностью называется функция, областью |
||||||||||
определен я которой является |
множество натуральных чисел 1, 2, 3. |
|||||||||
1. a бА, т. е. a 1; a ; a ; . |
||||||||||
Элементы (члены) последовательности записываются в виде |
||||||||||
|
|
|
|
f 1, f 2 , f 3 , ; |
|
|
||||
|
|
|
или |
an a1, a2, a3, ; |
||||||
|
|
|
или |
xn x1, x2, x3, . |
||||||
Примеры: |
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
1 |
|
|
1 |
||
n |
|
|
|
1 |
2 |
|
|
3 |
|
|
|
2 |
|
3 |
|||||||
|
n |
|
|
|
|
|
||||
2. |
|
an 1 n , |
|
т.е. |
|
a1 1; a2 1; a3 1, ; a51 1; |
||||||
a200 1,... . |
1 , т. е. a 1;a |
|
|
|
И |
|||||||
3. a |
n |
a 1, . |
|
|
||||||||
|
1 |
|
|
|
|
2 |
Д3 |
|||||
Последовательность an называется ограниченной, если суще- |
||||||||||||
ствует число М, такое, что |
|
an |
|
M при всех n (рис. 64). |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
an |
х |
|
|
|
|
( |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
М |
|
|
|
|
|
0 |
М |
||
Рис. 64
Пример
an n2 неограниченная последовательность.
125
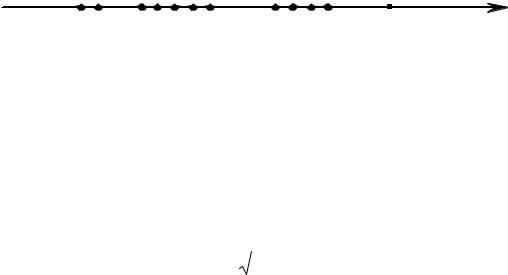
Число a |
называется пределом последовательности xn , если |
|||||||||||||||||
для любого числа 0 существует номер N , |
такой, что для всех |
|||||||||||||||||
n N выполняется неравенство |
|
xn a |
|
(рис. 65). |
||||||||||||||
|
|
|||||||||||||||||
Обозначение: a lim xn. |
|
|
|
|
|
|
|
|
|
|
||||||||
С |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
а |
|
|
|
|
|
|
|
х |
||||||
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
( |
|
|
|
|
|
|
|
) |
|
|
) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
если |
|
|
|
|
|
|
2 |
|
|
1 |
||||||||
Рис. 65 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Последовательность n |
называется бесконечно малой (б. м.), |
|||||||||||||||||
lim n 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n |
|
бА |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пр мер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|||||
|
|
, k |
0 |
; |
|
; |
; |
|
|
|
; б.м. последовательности. |
|||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||
nk |
|
|
|
|
n |
n2 |
|
|
|
|
|
|
||||||
Свойства б. м. последовательностей: |
|
|
|
|||||||||||||||
1. |
lim xn a xn a б.м. |
|
|
|
|
|
|
|||||||||||
|
x |
|
|
|
|
|
|
|
Д |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
Если an и n б.м., то an bn б.м. |
|
3. |
Если an и n б.м., то an bn б.м. |
|
4. |
И |
|
Если an ограниченная последовательность, n |
б.м., то |
|
an n б.м.
Последовательность an называется положительно бесконечно большой (п. б. б.), если для любого числа М > 0 существует номер N (M), такой, что при всех n N выполняется неравенство an M .
Обозначение: lim an (п. б. б.).
n
126
Пример
n2 п. б. б.
Последовательность an называется отрицательно бесконечно большой (о. б. б.), если для любого числа М< 0 существует номер N (M), такой, что при n N выполняется неравенство an M .
Обозначение: lim an (о. б. б.).
n
Последовательность an называется бесконечно большой (б. б.), |
|||||||||||||||||||
последовательность, составленная из величин |
|
an |
|
, является |
|||||||||||||||
|
|
||||||||||||||||||
Сп. б. б. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обозначен е: lim an . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пр мер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
|
., не о. . б., а б. б. последовательность. |
|||||||||||||||||
1 n |
|
это не п. . |
|
||||||||||||||||
Основные теоремы о последовательностях, имеющих предел |
|||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
||||||||||
Теорема 1 (связь |
.м. и |
. |
|
. последовательностей): |
|||||||||||||||
1. Если an б.м., то |
1 |
|
|
б.б. |
1 |
|
. |
||||||||||||
a |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||
|
|
|
Аn |
||||||||||||||||
2. Если an б. б., то |
1 |
|
|
б. м. |
1 |
0 . |
|||||||||||||
|
a |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n |
|
|
||||||||||
Теорема 2. Если |
lim x |
n |
|
aД, то x ограниченная последо- |
|||||||||||||||
вательность. |
|
|
n |
|
|
|
|
|
|
|
|
n |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема 3. Если |
lim xn |
|
a; lim xn b, то a b. (Если после- |
||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
И |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
довательность имеет предел, то он единственный.) |
|||||||||||||||||||
Теорема 4. Если lim xn |
a; lim yn |
b, то |
|||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
1) |
lim xn yn a b; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
lim xn yn a b; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
127
