
- •Введение
- •Раздел 1. ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА
- •1.1. ЛИНЕЙНАЯ АЛГЕБРА
- •§1. Матрицы и действия с ними
- •§2. Определители
- •§3. Обратная матрица
- •§4. Крамеровские системы линейных уравнений. Метод Крамера
- •§5. Крамеровские системы линейных уравнений. Матричный метод решения систем линейных уравнений
- •§6. Ранг матрицы
- •§7. Системы линейных уравнений: общий случай
- •§8. Метод Гаусса
- •§9. Однородные системы
- •1.2. ВЕКТОРНАЯ АЛГЕБРА
- •§12. Базис и координаты
- •§13. Орт и направляющие косинусы
- •§15. Векторное произведение векторов
- •§16. Смешанное произведение векторов
- •§17. Основные понятия
- •§18. Полярная система координат
- •§19. Прямая на плоскости
- •§20. Кривые второго порядка. Эллипс
- •§21. Гипербола
- •§22. Парабола
- •§23. Плоскость
- •§24. Прямая в пространстве
- •§25. Поверхности второго порядка
- •Раздел 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •3.2. ТЕОРИЯ ПРЕДЕЛОВ
- •§ 29. Предел функции
- •§ 30. Основные свойства пределов функции
- •§ 31. Замечательные пределы
- •3.3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- •§ 32. Непрерывность функции в точке
- •§ 33. Точки разрыва графика функции и их классификация
- •§ 34. Определение производной функции
- •§ 35. Производные некоторых элементарных функций
- •§ 36. Основные правила дифференцирования
- •§ 39. Дифференциал функции
- •§ 40. Производные и дифференциалы высших порядков
- •§ 41. Правило Лопиталя
- •§ 43. Нахождение наибольшего и наименьшего значений функции на отрезке
- •§ 44. Схема исследования функции и построения графика
- •§ 45. Формула Тейлора
- •Задачи для самостоятельного решения
- •Библиографический список
§18. Полярная система координат
Полярная система координат – это система координат на плоскости, в которой каждая точка плоскости однозначно определяется двумя числами – полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда связь между точками проще изобразить в виде радиусов и углов. В декартовой прямоугольной с стеме координат такие соотношения можно получить, только пр меняя тригонометрические уравнения.
плоскости
Полярная с стема координат определяется точкой O, называе-
мой полюсом, |
|
лучом, исходящим из полюса, называе- |
С |
|
|
мым полярной осью. Задается также единица масштаба. Любая точка |
||
М на |
определяется двумя полярными координатами: по- |
|
бА |
||
лярным рад усом r полярным углом |
(рис.17). |
|
Y |
M |
|
|
r |
|
|
y |
|
|
|
X |
|
|
|
O |
Д |
|
x |
|
|
Рис. 17
Полярным радиусом r точки M называется расстояние от полюса O до точки M (r = |OM|). Полярным угломИназывается угол между полярной осью и вектором OM (рис.17). Полярный угол измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Определённая таким образом радиальная координата r может принимать значения от нуля до бесконечности, а угловая координата может быть любой. Обычно полагают 0 ≤ < 2 π ,
или − π < ≤ π.
Полярные координаты начала координат − точки O: r = 0, угол не определен. У остальных точек r > 0 и угол определен с точностью до 2π.
69

Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось − с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты r и формулами
x= r cos ;
y= r sin .
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
Полярные коорд наты r и точки M выражаются через ее |
|||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
||
декартовы коорд наты x |
y формулами |
|
|
|
|
||||||||
|
|
|
r x |
2 |
y |
2 |
; |
||||||
|
|
|
|
|
|
|
|
||||||
|
бАsin = |
||||||||||||
|
|
|
tg |
y |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
|
|
|
|
||
Из эт х формул можно получить соотношения для вычисления |
|||||||||||||
угла ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos = |
|
|
|
x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x2 + y2 ; |
||||||||
|
|
|
Д |
||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
||
|
|
|
|
|
x2 + y2 . |
||||||||
Пример |
|
|
|
|
|
|
|
|
|
|
|
И |
|
Архимедова спираль – плоская кривая, сформированная траек- |
|||||||||||||
торией произвольной точки, которая |
|
равномерно движется по лу- |
|||||||||||
чу, берущему свое начало в O. Одновременно с этим луч равномерно вращается вокруг O. Таким образом, расстояние r пропорционально углу оборота луча. Обороту луча на одинаковый угол соответствует одно и то же увеличение расстояния r (рис. 18).
70

Симеет в д
Рис. 18
точки r = a ,
Уравнен е арх медовой спирали в полярной системе координат
где a – сдв оборотег M по лучу при на угол, который равен одному рад ану.
Обороту прямой на 2π соответствует смещение по лучу на 2aπ –
на шаг сп рали.
Если мы поворачиваем луч против движения часовой стрелки, получаем правую спираль, если поворачиваем по часовой стрелке, –
левую спираль. |
|
В природе форму спирали |
рхимеда имеют большинство рако- |
Даже |
|
вин. Семена в корзине подсолнечника расположены по спирали. Спи- |
|
раль можно увидеть,Анапример, в кактусах, ананасах. Ураган закручи- |
|
вается спиралью. По спирали разбегается стадо оленей. войной спи- |
|
ралью закручена молекула ДНК. |
галактики сформированы по |
принципу спирали. |
И |
В III в. до н.э. Архимед на основе своей спирали изобрёл винт, который успешно применяли для передачи воды в оросительные каналы из водоёмов, расположенных ниже. Позже на основе винта Архимеда создали шнек («улитку»). Его очень известная разновидность
– винтовой ротор в мясорубке. Шнек используют в механизмах для перемешивания материалов различной консистенции. В технике нашли применение антенны в виде спирали Архимеда. Самоцентрирующийся патрон выполнен по спирали Архимеда. Звуковые дорожки на CD и DVD дисках также имеют форму спирали Архимеда.
71
§19. Прямая на плоскости
На плоскости прямая чаще всего задается уравнениями вида
(прил.13)
1) |
y kx b – уравнение прямой с угловым коэффициентом |
|||||||
(для прямых, не параллельных оси Oy); |
||||||||
2) |
Ax By C 0 общее уравнение прямой; |
|||||||
и |
||||||||
С3) r |
r |
|
а |
t векторное уравнение; |
||||
|
|
0 |
|
|
|
|
||
|
x x0 |
|
lt; |
|||||
4) |
|
бА |
||||||
|
|
y y |
0 |
mt. |
||||
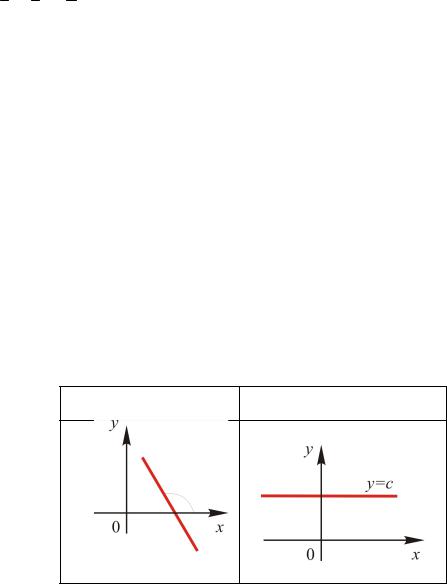
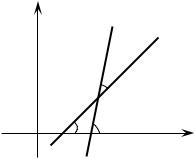
1) Уравнен е прямой с угловым коэффициентом
Тангенс угла наклона прямой к положительному направлению оси Ox будем называть угловым коэффициентом этой прямой
|
k = tg . |
|
Возможны следующие случаи положения прямых в зависимости |
||
от k (рис. 19). |
И |
|
k 0 |
||
Дk 0 |
||
Рис. 19 (начало)
72
k 0 |
k |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис |
|
|
|
|
|
|
|||
|
|
|
Рис. 19 (окончание) |
|
|
|
|
|
|
|
|
Вывод уравнения прямой |
|
|
|
|
|
||
бА |
и M1 |
x1, y1 |
|||||||
Пусть звестны координаты двух точек |
M0 |
x0, y0 |
|||||||
на прямой (р с. 20). Из |
. 20 очевидно, что k |
y1 y0 |
. |
|
|
||||
|
|
|
|
|
x1 x0 |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y1 |
|
M1 |
|
|
|
|
|
|
|
y0 |
|
M0 |
|
|
|
|
|
|
|
|
|
Д |
||||||
|
|
|
|
И |
|||||
|
|
0 |
x0 |
x1 |
x |
|
|
|
|
|
|
|
Рис. 20 |
|
|
|
|
|
|
Пусть теперь известен угловой коэффициент прямой k |
и коор- |
||||||||
динаты точки M0 x0, y0 |
на прямой. Пусть M x,y произвольная |
||||||||
точка на прямой. |
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
ky y0 x x0
73
или
y y0 k x x0
это уравнение прямой, проходящей через точку M0 x0, y0 .
Раскроем скобки:
y kx y0 kx0.
Теперь обознач м b y0 kx0 , тогда получим |
||||||||
С |
y kx b |
|
|
|
||||
|
|
|
|
|||||
это уравнен е прямой с угловым коэффициентом. |
||||||||
и |
|
|
|
|
|
|
|
|
бА |
||||||||
Ч сло b называется сво одным членом. |
||||||||
Геометр чески ч сло b равно отрезку, отсекаемому прямой на |
||||||||
оси Oy(рис. 21). |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|||
|
|
|
b |
|
|
|
||
|
|
|
|
|
||||
|
|
|
|
Д |
||||
|
|
|
||||||
|
|
|
||||||
|
|
Рис. 21 |
И |
|||||
|
|
|
|
|
|
|||
Уравнение прямой, проходящей через две заданные точки |
||||||||
Пусть известны координаты точек |
M0 x0, y0 и M1 x1, y1 , ле- |
|||||||
жащих на прямой. Так как k |
y y0 |
и |
k |
y1 y0 |
, то, приравнивая |
|||
|
|
|
|
|||||
|
|
x x0 |
|
x1 x0 |
||||
выражения, получаем уравнение
74
|
|
|
y y0 |
|
|
|
|
y1 y0 |
|
|
|||||
или |
|
|
x x0 |
|
x1 x0 |
|
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
y y0 |
|
|
|
x x0 |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
y1 y0 |
|
|
x1 x0 |
|
||||||||||
|
|
|
|
|
|||||||||||
Пр мер |
|
|
прямой, проходящей через точки M0 2,3 |
||||||||||||
остав ть |
|
|
|||||||||||||
уравнениеy 3 |
x 2; |
|
|||||||||||||
и M1 1, 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решен е. Подставляем координаты точек в уравнение и делаем пре- |
|||||||||||||||
образован я: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
бА |
|||||||||||||||
|
|
|
|
1 3 |
|
|
|
1 2 |
|
||||||
|
|
|
|
y 3 |
x 2; |
|
|||||||||
|
|
|
|
4 |
|
|
|
1 |
|
||||||
|
1 y 3 4 x 2 . |
||||||||||||||
После упрощений получаем уравнение прямой в виде с угловым |
|||||||||||||||
коэффициентом y 4x 5. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Угол между прямыми |
||||||||||||||
Даны уравнения двух прямыхД |
|||||||||||||||
|
1 : |
y k1 x b1; |
И |
||||||||||||
|
|
||||||||||||||
|
2 : |
y k2 x b2 . |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем угол |
между прямыми 1, 2 |
. |
|||||||||||||
Из рис. 22 получаем, что 2 1.
75
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
O |
|
|
|
1 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
Рис. 22 |
|
|
|
|
|
||||
Используем тр гонометрическую формулу |
|||||||||||||||||
|
|
бА |
|||||||||||||||
|
|
|
|
|
tg tg |
|
|
tg |
2 tg 1 |
. |
|||||||
и2 |
|
|
1 |
1 tg 1tg 2 |
|||||||||||||
Так как, по определению углового коэффициента, tg =k, то |
|||||||||||||||||
|
|
|
|
|
|
tg |
|
|
|
k2 k1 |
|
|
|
||||
|
|
|
|
|
|
, |
|
. |
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
1 k k |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Д |
||||||||
Это формула для нахождении угла между прямыми. |
|||||||||||||||||
Наличие модуля в формуле позволяет находить сразу острый |
|||||||||||||||||
угол между прямыми. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следствием этой формулы являются условия параллельности и |
|||||||||||||||||
перпендикулярности прямых. |
|
|
|
|
|
|
|
|
|
И |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Условие параллельности прямых |
||||||||||||
|
|
|
|
|
|
1 || 2 k1 k2 . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, |
если 1 || 2 , |
то 1 2 0; tg = 0. То есть |
|||||||||||||||
|
|
|
|
0 |
k1 k2 . |
|
|
|
|
|
|
|
|
|
|||
tg 1, 2 |
|
k2 k1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 k k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
76
Условие перпендикулярности прямых
1 2 k1 k2 1.
Действительно, если |
|
|
|
|
|
|
|
|
|
|
|
|
= 900 , tg900 не суще- |
||||||||
1 |
|
2 |
, то = |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
ствует. То есть tg |
|
|
|
|
k2 k1 |
|
|
|
не существует |
знаменатель |
|||||||||||
, |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
2 |
|
|
1 k k |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
дроби не определен |
|
k1k2 |
= – 1. |
|
|
|
|
|
|
|
|
|
|||||||||
причем |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
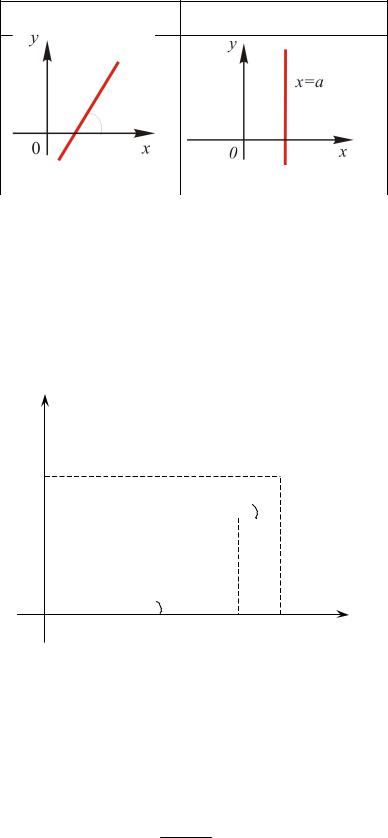
С2) О щее уравнение прямой |
|
||||||||||||||||||||
Всякое уравнен е первой степени вида |
|
Ax By C 0 (где |
|||||||||||||||||||
|
общим |
|
|
|
|
|
|||||||||||||||
A,B,C – постоянные, |
|
|
|
|
|
|
|
A2 |
B2 0) определяет на плоскости |
||||||||||||
прямую. Это уравнен е называется |
уравнением прямой. |
||||||||||||||||||||
Частные случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
А |
|
|||||||||||||||||
1. Прямая, определяемая уравнением Ax By 0 (С = 0, урав- |
|||||||||||||||||||||
нение можно прео разовать к виду y kx), |
|
проходит через начало |
|||||||||||||||||||
координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Прямая, определяемая уравнением y b ( |
= 0), параллельна |
||||||||||||||||||||
оси Ох. Прямая, определяемая уравнением y 0, это ось Ох. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
Дy |
|||||||||
3. Прямая, определяемая уравнением |
x a (В |
= 0), параллельна |
|||||||||||||||||||
оси Оу. Прямая вида x 0 |
это ось Оу. |
|
|
|
|
|
|||||||||||||||
4. Если A 0; |
|
B 0; C 0, то уравнение можно преобразовать |
|||||||||||||||||||
к виду уравнения прямой «в отрезках»: |
И |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
||
Числа a,b – это отрезки, отсекаемые прямой на координатных осях (рис. 23).
77

y
|
|
|
b |
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Рис. 23 |
|
|
|
|
|
|
|
|
|
|
||||
Расстояние от точки до прямой |
|
|
|
||||||||||||||
рисd |
0 |
2 |
|
0 |
2 . |
и точку M0 |
x0 |
, y0 |
|
||||||||
Рассмотр м прямую |
Ax |
By |
C |
0 |
|||||||||||||
( . 24). Расстоян е от точки до прямой находят по формуле |
|
|
|
||||||||||||||
бА |
|
|
|
|
|
||||||||||||
|
|
|
|
Ax By |
|
C |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B |
|
|
|
|
|
|
|
|
|||
|
|
|
|
d |
|
M0 x0,y0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Д |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
Ax+By+C=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 24
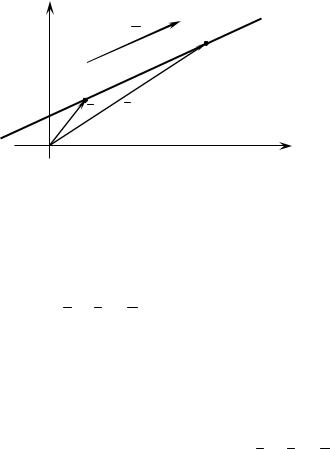
3) Векторное уравнение прямой
Рассмотрим прямую и вектор a , m 0, параллельный прямой. Всякий такой вектор называется направляющим.
Пусть на прямой даны две точки: M0 x0, y0 и M x,y . Тогда |
|
векторы r0 = OM0 |
и r =OM называютсяИрадиусами-векторами точек |
M0 , M . Координаты радиусов-векторов совпадают с координатами точек: r0 x0, y0 ; r x, y .
Так как M0M || a , то M0M a t, где t – некоторое число (параметр).
78
С |
M0(x0,y0) |
|
|
|
|
|
|
|
a |
M(x,y) |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
r0 |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Рис. 25 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используем прав ло сложения векторов r r0 M0M (рис. 25). |
|||||||||||||||||||||
Получ м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
r |
|
r0 |
at . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Это есть векторное уравнение прямой. |
|||||||||||||||||||||
|
4) Параметрическое уравнение прямой |
||||||||||||||||||||
Запишем теперь векторное уравнение прямой |
r |
|
r0 |
at в коор- |
|||||||||||||||||
динатах |
бА |
||||||||||||||||||||
|
|||||||||||||||||||||
|
|
x, y |
|
x0, y0 |
,m t . |
||||||||||||||||
Выпишем равенства для каждой из координат, получим |
|||||||||||||||||||||
|
|
|
x x |
t; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Д0 |
|||||||||||||||
|
|
|
|
|
|
|
mt. |
И |
|||||||||||||
|
|
|
y y0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Это параметрическое уравнение прямой.
Здесь x0, y0 – координаты точки на прямой, ,m – координа-
ты направляющего вектора. |
|
|
Примеры: |
|
|
1. |
Написать уравнения прямых, проходящих |
через точку |
M0 2, 1 |
параллельно, перпендикулярно и под углом |
45 к прямой |
y 2x 4.
79
Решение. Для решения задачи используем уравнение прямой, проходящей через заданную точку y y0 k x x0 . Подставим в это уравнение координаты точки M0 2, 1 , получим уравнение y 1 k x 2 .
|
|
Определим теперь угловой коэффициент k |
прямой. По усло- |
||||||||||||||||||||||||||||
вию, прямая параллельна прямой y 2x 4, поэтому, используя кри- |
|||||||||||||||||||||||||||||||
терий параллельности прямых, |
находим, |
|
что k 2. |
|
Подставляем в |
||||||||||||||||||||||||||
уравнен е: y 1 2x 4 2x 4 y 1 0 2x y 5= 0 – нашли |
|||||||||||||||||||||||||||||||
уравнен е прямой, параллельной данной. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Если |
|
скомая прямая перпендикулярна данной, |
то, из критерия |
||||||||||||||||||||||||||
Спрямых |
1 |
|
2 |
k |
|
k |
2 |
1, |
находим |
k |
1 |
. |
|||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
Подстав м найденное значение k |
|
в уравнение |
y 1 k x 2 , |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ортогональности |
|
|
|
|
|
|
|
|
|
|
|
|
– это |
||||||||||||||||||
получ м |
y |
1 |
2 |
x 2 x 2 2y 2 0 x 2y 0 |
|||||||||||||||||||||||||||
уравнен е прямой, перпендикулярной прямой y 2x 4. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
Определим далее угловой коэффициент прямой, проходящей |
|||||||||||||||||||||||||||||
под |
углом |
|
|
45 |
к |
данной |
|
прямой |
|
y 2x 4, |
|
по |
формуле |
||||||||||||||||||
|
|
|
k2 k1 |
|
. |
Подставляя |
|
в |
|
|
эту |
формулу |
= 45 , |
получим |
|||||||||||||||||
tg |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
1 k1k |
2 |
|
бА |
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 k1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
(так как угловой коэффициент данной прямой k 2). |
||||||||||||||||||||||||||||
1 2k1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Имеем |
|
|
|
1 2k |
2 k |
|
или |
k |
|
3. |
|
Тогда |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
3 |
|
|
1 |
|
|
|
|
|
||
y 3x 5 0 и |
3y x 5 0 |
– |
Д |
|
|
|
|||||||||||||||||||||||||
уравнения прямых, проходящих под |
|||||||||||||||||||||||||||||||
углом 45 |
к данной. |
|
|
|
|
|
|
проходящей через точки A1 5, 1 и |
|||||||||||||||||||||||
|
|
2. Найти уравнение прямой, |
|||||||||||||||||||||||||||||
A2 2,5 . И
Решение. Воспользуемся уравнением прямой, проходящей через две
точки |
y y0 |
|
x x0 |
: |
y1 y0 |
|
|||
|
|
x1 x0 |
||
80

x 5 y 1 x 5 y 1 2 x 5 y 1 2 x 10 y 1 0
2 5 |
|
|
5 1 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 x y 9 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Найти угол между прямыми y 3x и y 2x 5. |
|
|
|
|||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Для вычисления угла между прямыми используем формулу |
||||||||||||||||||||||||||||
tg |
|
|
k2 k1 |
|
. Так как k |
3; |
k |
2 |
2, то tg |
3 2 |
|
5 |
|
1. От- |
||||||||||||||
|
|
1 k1k2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 6 |
|
5 |
|
|
|
||||||||
сторонууравненияАС; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
сюда |
arctg |
1 |
1 |
45 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Заданы верш ны |
|
треугольника |
АВС: |
A(3,1), B(1,7),С(6,3). |
||||||||||||||||||||||||
Требуется: |
б |
|
|
|
|
АВС; |
|
|
|
|||||||||||||||||||
1) состав |
ть |
|
|
|
|
всех сторон треугольника |
|
|
|
|||||||||||||||||||
2) состав ть уравнение высоты, опущенной из вершины В на |
||||||||||||||||||||||||||||
3) состав ть уравнение медианы, проведенной из вершины С; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
||||||||||||||
4) найти расстоян е от вершины |
С до стороны АВ; |
|
|
|
||||||||||||||||||||||||
5) найти угол между сторонами |
С и В; |
|
|
|
|
|
|
|
|
|||||||||||||||||||
6) вычислить периметр треугольника |
|
ВС. |
|
|
|
|
|
|
|
|
||||||||||||||||||
Решение. Построим в декартовой системе координат треугольник |
||||||||||||||||||||||||||||
АВС с заданными координатами вершин (рис. 26). |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
B |
Д |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
M |
H |
C |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 26 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) Для нахождения уравнения сторон треугольника воспользуем- |
||||||||||||||||||||||||||||
ся уравнением прямой, проходящей через две точки |
x x1 |
|
|
y y1 |
. |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x1 |
|
y2 y1 |
||||
81
|
|
|
Уравнение |
прямой |
АВ: |
|
x 3 |
|
|
y 1 |
, |
|
или |
|
|
|
x 3 |
|
|
|
|
y 1 |
, |
или |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
6x 2y 20 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 3 |
|
|
|
|
7 1 |
|
|
|
|
|
|
|
|
|
2 |
6 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
y 1 |
|
|
|||||||||||||||||||||||||||
|
|
|
Уравнение |
|
|
|
|
прямой |
|
АС: |
|
|
|
|
, |
или |
|
|
|
|
|
, |
или |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
6 3 |
|
|
3 1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||
3y 2x 3 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
y 7 |
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
y 7 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Уравнен е прямой ВС: |
|
, |
|
|
или |
|
|
, или |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4x 5y 39 0. |
|
|
|
|
|
|
|
|
6 1 |
|
|
3 7 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
сти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2) Пусть АН |
– высота, опущенная из вершины А на сторону ВС. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Найдем ее уравнен е в виде y y0 |
k x x0 . Так как высота опуще- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
на из точки А, |
то x0 |
xA 3; y0 |
|
yA |
|
1. Воспользуемся теперь урав- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
бА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
нением стороны |
ВС |
: 4x |
5y 39 0 и условием перпендикулярно- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
прямых |
1 |
|
2 |
k k |
2 |
1. Найдем, что |
x 1 |
|
y 7 |
– уравне- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
5 |
|
|
|
|
||||||||||||||||||
ние высоты АН. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3) Пусть АМ – медиана, проведенная из вершины С на сторону |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
АВ. По определению медианы, точка М делит отрезок АВ пополам. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Координаты середины отрезка находим по формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xM |
= |
xA |
+ xB |
|
= |
3+1 |
= 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yM |
|
= yA + yB |
= |
1+7 = 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для нахождения уравнения медианы СМ воспользуемся уравне- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нием прямой, проходящей через две точки: |
|
|
x x1 |
|
|
y y1 |
. Так как |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x2 x1 |
y2 y1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
С(6,3), |
M(2,4), то |
|
x 6 |
|
y 3 |
или |
|
|
x 6 |
|
|
y 3 |
– уравнение медиа- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 6 |
|
4 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ны СМ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||||||||||||||||||
|
|
|
4) Расстояние от вершины С до стороны АВ находим по формуле |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d |
|
|
Ax0 |
By0 C |
|
|
. Так как |
6x 2y 20 0– общее уравнение сторо- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A2 B2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ны АВ, |
то А=6; В=2; С= –20; x0 xC 6; y0 |
yC 3. Тогда |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
82
