
- •Введение
- •Раздел 1. ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА
- •1.1. ЛИНЕЙНАЯ АЛГЕБРА
- •§1. Матрицы и действия с ними
- •§2. Определители
- •§3. Обратная матрица
- •§4. Крамеровские системы линейных уравнений. Метод Крамера
- •§5. Крамеровские системы линейных уравнений. Матричный метод решения систем линейных уравнений
- •§6. Ранг матрицы
- •§7. Системы линейных уравнений: общий случай
- •§8. Метод Гаусса
- •§9. Однородные системы
- •1.2. ВЕКТОРНАЯ АЛГЕБРА
- •§12. Базис и координаты
- •§13. Орт и направляющие косинусы
- •§15. Векторное произведение векторов
- •§16. Смешанное произведение векторов
- •§17. Основные понятия
- •§18. Полярная система координат
- •§19. Прямая на плоскости
- •§20. Кривые второго порядка. Эллипс
- •§21. Гипербола
- •§22. Парабола
- •§23. Плоскость
- •§24. Прямая в пространстве
- •§25. Поверхности второго порядка
- •Раздел 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •3.2. ТЕОРИЯ ПРЕДЕЛОВ
- •§ 29. Предел функции
- •§ 30. Основные свойства пределов функции
- •§ 31. Замечательные пределы
- •3.3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- •§ 32. Непрерывность функции в точке
- •§ 33. Точки разрыва графика функции и их классификация
- •§ 34. Определение производной функции
- •§ 35. Производные некоторых элементарных функций
- •§ 36. Основные правила дифференцирования
- •§ 39. Дифференциал функции
- •§ 40. Производные и дифференциалы высших порядков
- •§ 41. Правило Лопиталя
- •§ 43. Нахождение наибольшего и наименьшего значений функции на отрезке
- •§ 44. Схема исследования функции и построения графика
- •§ 45. Формула Тейлора
- •Задачи для самостоятельного решения
- •Библиографический список
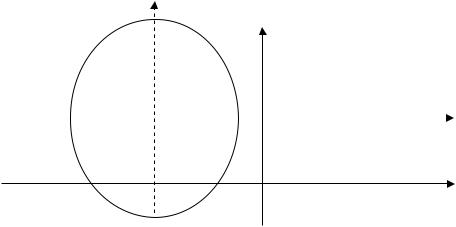
Для построения кривой перенесем начало координат в точку (–2,2), т.е. сделаем замену :
С |
|
x x x0 x 2; |
|
||||
|
|
|
|
|
|||
|
y y y0 y 2. |
|
|||||
|
|
|
уравнение кривой будет иметь кано- |
||||
В системе координат 0xy |
|
||||||
ническ й в д |
x 2 |
|
y 2 |
1 (рис. 36). |
|
||
|
|
|
|||||
и |
|
|
|
||||
5 |
|
20 |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y |
|
бА |
x |
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
-2 |
|
-1 0 |
x |
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
Рис. 36 |
|
2.2. АНАЛИТИЧЕСК Я ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§23. Плоскость
Назовем нормалью к плоскости вектор, перпендикулярный к
этой плоскости (рис. 37). Пусть |
известны координаты нормали: |
||
|
|
A,B,C . |
|
|
n |
|
|
|
|
Уравнением поверхности в пространстве Oxyz называется урав- |
|
нение, связывающее переменные |
x,y, z, которомуИудовлетворяют |
||
координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности (прил. 17).
97

|
|
|
|
|
|
|
|
|
|
|
n |
A,B,C |
|
|
|
||
С |
|
|
|
|
|
M x,y,z |
|
|
|
|
|||||||
|
|
|
|
M0 x0,y0,z0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Рис. 37 |
|
|
|
|
||||
–плоскостиэто уравнен е , проходящей через точку M |
0 x0, y0 |
,z0 |
|
||||||||||||||
|
|
|
Пусть точки |
M0 |
M лежат на плоскости (см. рис. 37). Тогда |
||||||||||||
|
n |
|
M0M |
, знач т, |
х скалярное произведение равно нулю: |
|
|
|
|||||||||
|
|
|
|
бА |
|
|
|
||||||||||
|
|
|
|
|
A x x0 |
B y |
y0 C z z0 0 |
|
|
|
|||||||
перпенд кулярно вектору n A,B,C . |
|
|
|
|
|||||||||||||
|
|
|
|
Основные виды уравнения плоскости |
|
|
|
||||||||||
|
|
|
Основными видами уравнений плоскости являются: |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Д |
,z0 |
|
|||||
|
|
|
1. Уравнение плоскости, проходящей через точку M |
0 x0, y0 |
|||||||||||||
перпендикулярно вектору |
n |
A,B,C , (рис. 38) |
|
|
|
||||||||||||
|
|
|
|
A x x0 B y y0 C z z0 0. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
N A,B,C |
И |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 38
2. Общее уравнение плоскости
Ax By Cz D 0,
98
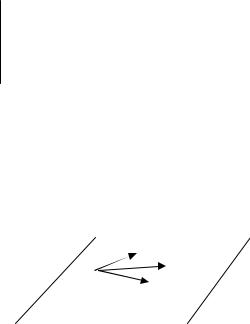
где A,B,C координаты нормали плоскости. Это уравнение полу-
чается из уравнения плоскости A x x0 B y y0 C z z0 0 после раскрытия скобок и обозначения D Ax0 By0 Сz0.
3. Уравнение плоскости, проходящей через три заданные точки
С |
, y2,z2 и M3 x3, y3 |
,z3 , |
|
|
M1 x1,y1,z1 , M2 x2 |
|
|||
|
x x1 |
y y1 |
z z1 |
|
|
x2 x1 |
y2 y1 |
z2 z1 |
0. |
ние |
y3 y1 |
z3 z1 |
|
|
|
x3 x1 |
|
||
Для вывода этого вида уравнения плоскости рассмотрим произ- |
|||||||||||||
вольную точку M x, y,z плоскости. Векторы |
|
, |
|
и |
|
|
|||||||
M1M |
M1M2 |
M1M3 |
|||||||||||
бА |
|||||||||||||
лежат в плоскости, то есть компланарны, и их смешанное произведе- |
|||||||||||||
равно нулю (р с. 39). |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
M3 |
|
|
|
|
|
|
|
|
M1 |
|
|
M2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
Д |
||||||||||
|
|
Рис. 39 |
|
|
|
|
|
|
|
||||
4. Уравнение плоскости в отрезках |
И |
||||||||||||
|
x y |
|
z |
||||||||||
|
|
+ |
|
+ |
|
=1, |
|||||||
|
a |
b |
c |
|
|
|
|
|
|
|
|||
где a,b,c величины отрезков, |
отсекаемых плоскостью на коорди- |
||||||||||||
натных осях Ox,Oy и Oz соответственно (рис. 40).
99

Z
c
С |
|
|
|
|
|
|
|
|
|
|
|
|
b |
Y |
|||||
|
X |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
уравнения |
|
|
Рис. 40 |
|
|
|
|
|
|
||||||||||
|
получается из общего уравнения при |
||||||||||||||||||
Данный в д |
|
|
|
|
|
||||||||||||||
D ≠0; A ≠0; B ≠0; C ≠0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бА |
|||||||||||||||||||
|
Ax |
+ By +Cz + D |
= 0 |
; |
|
||||||||||||||
|
Ax By Cz D / : D ; |
||||||||||||||||||
|
Ax |
|
|
|
By |
|
Cz |
|
1; |
||||||||||
|
D |
|
D |
|
D |
|
|
|
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
z |
|
1. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
D A |
|
|
|
|
Д |
|||||||||||||
|
|
|
|
|
D B |
|
D C |
||||||||||||
После переобозначений получаем уравнение плоскости вида |
|||||||||||||||||||
|
|
|
|
x |
|
|
|
|
y |
z |
|
|
|
|
И |
||||
|
|
|
|
|
+ |
|
|
+ c =1. |
|||||||||||
|
|
|
|
a |
b |
|
|
||||||||||||
Частные случаи положения плоскости в пространстве
Рассмотрим частные случаи положения плоскости в пространст-
ве: |
|
|
плоскость || оси Ox |
1. Если A 0 |
|
By Cz D 0 |
|
(рис. 41). |
|
|
|
100

|
|
|
|
|
|
Z |
|
|
|
С |
|
|
|
|
Y |
|
|||
|
X |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
Если |
Рис. 41 |
|
|||||||
|
|
плоскость проходит через ось |
|||||||
Ox. |
Если A D 0 |
|
By Cz 0 |
||||||
2. |
B 0 Ax Cz D 0 плоскость || оси Oy (рис. 42). |
||||||||
|
|||||||||
|
бА |
||||||||
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
Рис. 42 |
|
|||
|
Если B D 0 |
|
|
Д |
|||||
Oy. |
3. Если |
C 0 |
|
Ax By D 0 |
плоскость || оси Oz |
||||
(рис. 43). |
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
Z |
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
Рис. 43 |
|
|||
Oz. |
Если C D 0 |
Ax By 0 |
плоскость проходит через ось |
||||||
4. Если D 0 Ax By Cz 0 плоскость проходит через |
|||||||||
|
|||||||||
начало координат (рис. 44). |
|
|
|
|
|||||
101

|
|
|
Z |
|
|
С |
|
|
|
Y |
|
X |
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 44 |
|
|
5. Если A B 0 |
Cz D 0 |
плоскость || осям Ox и Oy |
|||
рис |
|
|
|
||
( . 45). |
|
|
|
|
|
|
|
|
Z |
|
|
|
бА |
||||
|
|
|
|
|
Y |
|
|
X |
|
|
|
|
|
|
Рис. 45 |
|
|
Уравнение z = 0 уравнение плоскости Oxy. |
|||||
6. Если A C 0 |
By D 0 плоскость || осям Ox и Oz |
||||
(рис. 46). |
|
|
Д |
||
|
|
|
|||
|
|
|
Z |
|
|
|
|
|
|
|
Y |
|
|
X |
|
Z |
И |
|
|
|
|
|
|
|
|
|
Рис. 46 |
|
|
Уравнение y = 0 уравнение плоскости Oxz. |
|||||
7. Если B C 0 |
Ax D 0 |
плоскость || осям Oy и Oz |
|||
(рис. 47). |
|
|
|
|
|
Y
X
Рис. 47
102
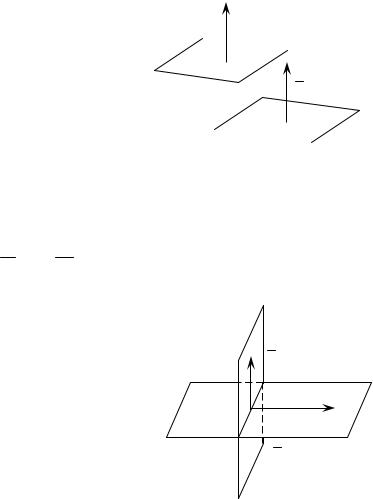
Уравнение x = 0 уравнение плоскости 0yz.
Взаимное расположение плоскостей
|
|
Пусть плоскости 1 и 2 заданы общими уравнениями |
|
||||||||||||
С |
|
A1x + B1y +C1z + D1 = 0; |
( 1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
A2x + B2 y +C2z + D2 = 0. |
( 2) |
||||||
нормалиn A ,B ,C |
|
||||||||||||||
|
|
Вза мное положение плоскостей зависит от положения их нор- |
|||||||||||||
малей: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1) 1// 2 |
|
плоскостей параллельны, то есть |
|
||||||||||
|
|
// |
|
|
|
A1 |
= |
B1 |
= C1 (рис. 48). |
|
|||||
|
n |
n |
|
|
|||||||||||
|
|
|
|
||||||||||||
1 |
|
|
2 |
бА2 |
|
||||||||||
|
|
|
A2 |
B2 |
C2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
n |
2 A2,B2,C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)1 2 нормали плоскостейДперпендикулярны, то есть
n1 n2 A1A2 + B1B2 +C1C2 = 0 (рис. 49)И.
1
n2 A2,B2,C2
2
Рис. 49
103
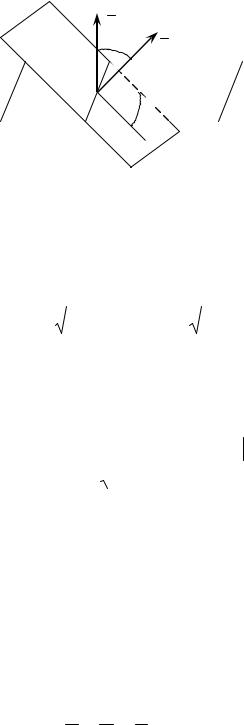
3)Угол между двумя плоскостями равен углу между нормалями
кэтим плоскостям (или дополняет этот последний до 180 ) (рис. 50).
С |
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 32 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Рис. 50 |
|
|
|
|
|
|
|
|
|
|||
бА |
|
|
||||||||||||||||||
Угол между двумя плоскостями вычисляется по формуле |
||||||||||||||||||||
cos |
n1 |
|
n2 |
|
|
A1 A2 B1 |
B2 С1С2 |
|
. |
|||||||||||
|
n1 n2 |
A2 |
B2 С2 |
A2 |
B2 |
С2 |
||||||||||||||
|
|
|
|
|
1 |
1 |
1 |
|
2 |
2 |
2 |
|
||||||||
4) Расстояние от точки M x1, y2,z1 до плоскости Ax By Cz |
||||||||||||||||||||
D 0 находят по формуле |
|
Д |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
d |
|
Ax1 By1 |
Cz1 D |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||
Примеры:
1. Построить плоскость по ее уравнению а) 4x 3y 6z 12 0.
Решение. Все коэффициенты в уравнении отличны от нуля, поэтому удобно преобразовать его к уравнению в отрезках (рис. 51):
x y z 1.
3 4 2
Теперь откладываем на координатных осях отрезки 3, 4, 2 и строим плоскость.
104
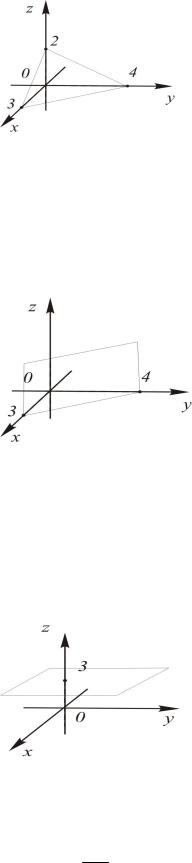
Рис. 51
оси |
|
б) 4x 3y 12 0. |
|
СРешен е. Уравнен е не содержит переменную z, значит, плоскость парал- |
|
лельна |
Oz, а ее направляющей служит прямая 4x 3y 12 0(рис. 52). |
в) z бА3. |
|
|
Рис. 52 |
Решение. |
Д |
Это плоскость, параллельная осям Ox и Oy, иначе говоря, парал- |
|
лельная плоскости Oxy, проходящая через точку z = 3 (рис. 53). |
|
|
И |
Рис. 53
2. Написать уравнение плоскости, проходящей через точку
A 2,5, 3 перпендикулярно векторуBC, если B 7,8, 1 и C 9,7,4 .
105

Решение. Найдем ВС 9 7,7 8,4 1 2, 1,5 . Воспользуемся уравнением плоскости, проходящей через данную точку:
|
|
|
A x x0 B y y0 C z z0 0. |
||||||||||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 x 2 1 y 5 5 z 3 0 2x y 5z 4 5 15 0 |
|||||||||||||||
Найти |
|
|
|
|
|
|
|
|
|
|
|||||
2x y |
5z 16 0. |
|
|
|
|
|
|
|
|
|
|
|
|||
С3. уравнение плоскости, проходящей через точки |
|||||||||||||||
M1 1,5, 7 , M2 3,6,3 и M3 2,7,3 . |
|
|
|
||||||||||||
|
бА |
|
|
||||||||||||
Решен е. Используем уравнение плоскости, проходящей через три |
|||||||||||||||
точки. Подстав м координаты данных точек: |
|
|
|
||||||||||||
|
|
x 1 |
y 5 |
z 7 |
|
|
x 1 |
y 5 |
z 7 |
0. |
|||||
|
|
3 1 |
6 5 |
3 7 |
0 |
4 |
1 |
10 |
|||||||
|
|
2 1 |
7 5 |
3 7 |
|
|
3 |
2 |
10 |
|
|||||
Раскладываем определитель по элементам первой строки, полу- |
|||||||||||||||
чаем |
|
|
|
|
|
Д |
|||||||||
|
|
2 x 1 2 y 5 z 7 0 2x 2y z 15 0. |
|||||||||||||
4. Найти расстояние от точки M0 2; 3;1 до плоскости, прохо- |
|||||||||||||||
дящей через три точки M1 1;1; 1 , M2 3;2; 4 , |
M3 2;1;0 . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
И |
||||
Решение. Составим уравнение плоскости, проходящей через три точ- |
|||||||||||||||
ки M1, M2, M3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x 1 |
y 1 |
z 1 |
|
|
|
|
|||||
|
|
|
|
3 1 |
2 1 |
4 1 |
0 |
|
|
||||||
|
|
|
|
2 1 |
1 1 |
0 1 |
|
|
|
|
|||||
или |
|
|
|
|
x 1 |
|
y 1 |
z 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
1 |
|
5 |
|
0. |
|
|
|||
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
||
106

Вычисляем определитель, раскладывая по первой строке:
x 1 |
1 |
5 |
y 1 |
2 |
5 |
z 1 |
2 |
1 |
0; |
|
0 |
1 |
|
1 |
1 |
|
1 |
0 |
|
С |
1 x 1 |
3 y 1 1 z 1 0; |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x 1 3y 3 z 1 0; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
уравнение |
|
|
|
|
|
|
проходящей через точки M1, |
||||||||||||||||||||||||
x 3y z 5 0 |
|
|
плоскости, |
|
|||||||||||||||||||||||||||
M2, M3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь |
спользуем формулу расстояния от точки до плоскости: |
||||||||||||||||||||||||||||||
|
|
|
б |
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
13 |
|
|
13 11 |
|
|
||||||||||||||||||
d |
|
2 3 3 1 5 |
|
|
|
2 9 6 |
|
|
13 |
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
12 32 1 2 |
11 |
|
11 |
|
|
|
|
|
11 |
|
|
11 |
|
|
||||||||||||
Итак, |
13 |
|
|
11 |
расстояние от M0 до плоскости. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. Найти |
|
|
|
угол |
между |
|
|
плоскостями |
x y 3z 4 0 и |
||||||||||||||||||||||
2x y z 8 0.
Решение. Угол между плоскостями совпадает с углом между их нормалями. Нормали плоскостей: n1 1, 1,3 ; n2 2,1, 1 .
Угол между нормалями найдём с помощью скалярного произведения
|
|
n n |
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||
|
|
2 |
|
|
|
|
2 1 1 Д1 3 1 2 2 |
|
|
||||||||||||||||||||||
cos |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
n1 |
|
n2 |
|
12 1 2 32 |
22 12 1 2 |
|
|
11 6 |
|
|
66 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получили |
cos |
|
|
|
|
; arccos |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
66 |
|
|
|
66 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
107
