
- •Введение
- •Раздел 1. ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА
- •1.1. ЛИНЕЙНАЯ АЛГЕБРА
- •§1. Матрицы и действия с ними
- •§2. Определители
- •§3. Обратная матрица
- •§4. Крамеровские системы линейных уравнений. Метод Крамера
- •§5. Крамеровские системы линейных уравнений. Матричный метод решения систем линейных уравнений
- •§6. Ранг матрицы
- •§7. Системы линейных уравнений: общий случай
- •§8. Метод Гаусса
- •§9. Однородные системы
- •1.2. ВЕКТОРНАЯ АЛГЕБРА
- •§12. Базис и координаты
- •§13. Орт и направляющие косинусы
- •§15. Векторное произведение векторов
- •§16. Смешанное произведение векторов
- •§17. Основные понятия
- •§18. Полярная система координат
- •§19. Прямая на плоскости
- •§20. Кривые второго порядка. Эллипс
- •§21. Гипербола
- •§22. Парабола
- •§23. Плоскость
- •§24. Прямая в пространстве
- •§25. Поверхности второго порядка
- •Раздел 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •3.2. ТЕОРИЯ ПРЕДЕЛОВ
- •§ 29. Предел функции
- •§ 30. Основные свойства пределов функции
- •§ 31. Замечательные пределы
- •3.3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- •§ 32. Непрерывность функции в точке
- •§ 33. Точки разрыва графика функции и их классификация
- •§ 34. Определение производной функции
- •§ 35. Производные некоторых элементарных функций
- •§ 36. Основные правила дифференцирования
- •§ 39. Дифференциал функции
- •§ 40. Производные и дифференциалы высших порядков
- •§ 41. Правило Лопиталя
- •§ 43. Нахождение наибольшего и наименьшего значений функции на отрезке
- •§ 44. Схема исследования функции и построения графика
- •§ 45. Формула Тейлора
- •Задачи для самостоятельного решения
- •Библиографический список
Свойства дифференциала функции
Если u (x), v (x) – дифференцируемые функции, тосправедливы следующиеформулы:
1. d (u + v) = du + dv. |
|
|
|
|
|
|
|
|
|
|||||
2. d (u v) = u dv + v du. |
|
|
|
|
|
|
|
|
|
|||||
вида |
|
|
|
|
|
|
|
|||||||
3. d |
u |
= |
du |
v u dv |
|
(v |
0). |
|
|
|
|
|||
Сv |
v2 |
|
|
|
|
|
|
|
|
|
||||
4. Инвар антность |
|
|
дифференциала. |
|
||||||||||
|
образом |
|
|
функции y = f(x), где |
||||||||||
Рассмотр м |
д фференциал |
сложной |
||||||||||||
x = (t), т. е. y = f ( (t)). |
|
|
|
|
|
|
|
|
|
|||||
Тогда dy = |
yt dt, но |
так как |
yt |
= yxxt , |
поэтому dy = yxxt dt. |
|||||||||
Учитывая, что |
xtdt = d x, |
|
получаем |
dy = yx d x = f (x) d x. |
||||||||||
Таким |
|
, дифференциал сложной функции y = f (x), где |
||||||||||||
x = (t), имеет вид dy = f |
(x) dx, |
такой же, как в том случае, когда x |
||||||||||||
является независимой переменной. Это свойство называется инвари- |
||||||||||||||
антностью формы дифференциала. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ДИФФЕРЕНЦИАЛЫ |
||||||
Посмотрите видеоА8. |
||||||||||||||
4.3. ПРОИЗВОДНЫЕ И |
|
|
|
|
|
ВЫСШ Х |
||||||||
ПОРЯДКОВ. ПРАВИЛО ЛОПИТАЛЯ |
|
И |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
§ 40. Производные и дифференциалы высших порядков |
||||||||||||||
Пусть функция f (x) определена и дифференцируема на некото- |
||||||||||||||
ром промежутке X, тогда ее производная |
|
f (x) также является функ- |
||||||||||||
цией от x на этом промежутке. Если |
f |
(x) |
имеет производную на |
|||||||||||
|
||||||||||||||
промежутке X, то эта производная называется производной второго порядка функции y = f (x) и обозначается y'' или f (x).
Итак, f (x) = ( f (x))'.
Вообще производной n-го порядка называется производная от производной (n – 1)-го порядка и обозначается y(n) или f (n) (x). Итак,
191
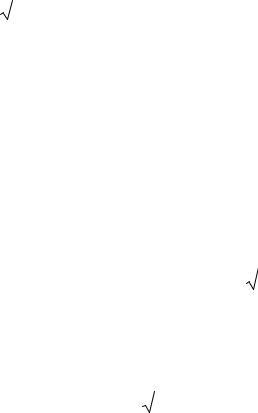
f (n) (x) = (f (n--1) (x))'.
Производные y'', y''', ... называются производными высших порядков.
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
С |
|
|
. Найти f (x) и f (4). |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1. f |
(x) = |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Решен е. |
Выч сляем производные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
и |
|
|
|
1/2 |
|
|
|
|
|
1 |
|
|
1/2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
f (x) |
= |
x |
|
|
|
|
|
|
|
= |
|
2 |
|
x |
|
|
; |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
f (x) = – |
1 |
x 3/2 |
; |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
бА |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
f (x) = |
3 |
|
|
x 5/2 = |
|
|
3 |
. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
x5 |
|
|
||||||
При x = 4 получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
f |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
(4) = |
|
|
|
|
|
|
|
|
|
= |
|
8 25 = |
256. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
8 |
4 |
5 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. Найти производную n-го порядка для функции y e3x. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
Решение. |
y |
|
3e |
|
; |
y |
|
3 3e |
|
3 |
|
|
|
e |
|
|
; |
|
|
y''' =3 |
e |
. |
|||||||||||||
По аналогии находим y |
(n) |
|
Дn 3x |
||||||||||||||||||||||||||||||||
|
|
= |
3 |
|
|
|
e . |
|
|
|
|
|
|
|
|||||||||||||||||||||
Механический смысл второй производной
Пусть путь S, пройденный телом по прямой за время t, выражается формулой S = f(t). Известно, что при этом скорость V в момент времени t равна производной от пути по времени: V = S (t). В момент времени t + t скорость получит приращение
V = V(t + t) – V(t).
192

Отношение V называется средним ускорением за время t.
t
Ускорением a в данный момент времени называется предел среднего ускорения, когда t 0:
С |
|
|
V |
|
|
|
|
|
|
||
|
|
a = |
lim |
|
|
, т.е. a = V'(t) = (S(t))' = S''(t). |
|||||
|
|
|
t 0 |
|
t |
|
|
|
|
|
|
|
ледовательно, ускорение при прямолинейном движении равно |
||||||||||
рассмотрению |
|
|
|
|
|
||||||
второй про зводной от пути по времени: |
|
|
|
|
|||||||
|
|
|
|
|
|
a = S'' (t). |
|
|
|
|
|
|
|
бА |
|
||||||||
|
Перейдем к |
|
|
|
|
дифференциалов высших порядков. |
|||||
|
Пусть y = f (x); |
x X. Дифференциал этой функции y = f '(x) dx |
|||||||||
является функц ей от x; dx – приращение аргумента x не зависит от x. |
|||||||||||
|
Д фференц ал от дифференциала функции называется диффе- |
||||||||||
ренциалом второго порядка и о означается d 2y или d 2f(x). |
|||||||||||
|
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2y = d (dy), |
|
|
|
|
||
но |
|
|
|
|
|
|
Д |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy= f (x)dx, |
И |
|||||
поэтому |
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
f |
|
2 |
||
|
|
d y = d ( f |
|
(x)dx) = ( f (x)dx)dx = |
|
(x)(dx) . |
|||||
Будем вместо (dx)2 писать dx2.
Дифференциалом n-го порядка называется дифференциал от дифференциала (n –1)-го порядка
d ny = d (d n – 1 y) = d (f (n – 1) (x)dxn – 1) = f (n)(x) dx n.
Итак,
d ny = f (n)( x) dx n.
193

Отсюда
|
|
(n) |
dn y |
|
|
f |
(x) = |
|
. |
|
dxn |
|||
Примеры: |
|
|
|
|
С |
|
|
|
|
1. Найти d 3y для функции y = cos2x. |
||||
Решен е. d 3y = y''' dx 3. Вычислим |
y''', находя последовательно y', |
|||
y'', y''': |
|
|
|
|
и |
|
|
||
|
y' = (cos2x)' = –2cosxsinx = –sin2x; |
|||
|
y'' = (–sin2x)' = –2cos2x; |
|||
бА |
||||
|
|
y''' = 4sin2x. |
||
Следовательно, d 3y = 4sin2x dx 3.
2. Вычислить с помощью дифференциала приближённое значение выражения 5
 31.
31.
Решение. Используем приближённое равенство
|
|
|
|
f (x) df |
(x) f |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
(x) x, |
||||||||||||||||||
верное при малых значениях x . Откуда |
|
|
|
|
|
|
|
|||||||||||||||
|
|
f (x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
0 |
x) Дf (x ) f (x ) x. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
||||
Преобразуем сначала исходное выражение |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
31 |
|
|
32 1 |
|
32(1 |
|
|
) 2 1 |
И. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
32 |
32 |
|
||||||||
|
f (x) 5 |
|
; x0 |
1; x |
1 |
. Производная равна |
||||||||||||||||
Положим |
x |
|||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|||
194
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
1 |
|
; f (1) |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Окончательно имеем 5 |
|
|
|
2(1 1 ( |
1 |
|
)) |
31 |
1 |
15 |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
31 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
32 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
16 |
|
|
|
|
|
|
|
||||||||
3. Найти вторую производную функции y |
|
|
|
|
|
x |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
||||||||||
Решен е. начала находим первую производную: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
x2 1 2x2 |
|
|
|
|
1 x2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Сy |
|
|
|
|
|
|
|
|
|
|
|
|
(x2 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
(x2 1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Теперь выч сляем вторую производную: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
1 x2 |
|
|
|
|
2x(x2 1)2 4x(1 x2)(x2 1) |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(x |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2x(x2 |
1) 4x(1 x2) |
|
|
2x3 2x 4x 4x3 |
|
|
|
|
2x3 |
|
2x |
. |
|||||||||||||||||||||||||||||||||||||
(x |
2 |
1) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
2 |
|
1) |
3 |
|
|
|
|
|
|
|
|
|
|
|
(x |
2 |
1) |
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
бАx a(t sint); |
|||||||||||||||||||||||||||||||||||||||||||||||||
4. Для параметрически заданной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
най- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y a(1 cost) |
||||||||||||||||||
тивторую производную y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Решение. Вычислим первую производнуюДданной функции. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yt |
= a sin t; |
|
|
xt |
|
= a (1 – cost); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
yx |
|
yt |
|
|
|
|
|
|
asint |
|
|
|
sint |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
= |
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
xt |
a(1 cost) |
(1 cost) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Итак, производная первого порядка имеет вид
195
