Реологические свойства казеина

а, H·cb/м2	b	0, H/м2	k, H·cn/м2	n	γmax, c–1	|εmax|, %	Т, К	W, %	t, сут
2430	0,342	0	2120	0,312	37	2,03	293	65	0
2480	0,574	6250	590	1,08	10,7	33,9	294	68	0,5
4290	0,262	11300	1160	0,571	60,2	12,0	293	66	2

Очевидно, казеин проявляет заметные неньютоновские свойства, причем с увеличением срока хранения растет предельное напряжение сдвига казеина. Свежий казеин практически не имеет предельного напряжения сдвига, его сдвиговое течение можно описать частным уравнением Гершеля – Балкли – уравнением Оствальда де Вале. Величины W и Т казеина, при которых проводили вискозиметрирование, соответствуют его технологическим параметрам до гранулирования, поэтому полученные реологические свойства могут быть использованы для расчета гранулятора. Можно сделать следующие выводы:

1. Кривые течения, полученные капиллярным вискозиметрированием свежего казеина 65 %-й влажности при температуре 293 К и скорости сдвига до 37 c^–1 , можно описать уравнением Оствальда де Вале.

2. Вязкостные свойства казеина со сроком хранения от 0,5 до 2 сут при комнатной температуре и скорости сдвига до 70 c^–1 описываются уравнением Гершеля – Балкли.

3. Предельное напряжение сдвига казеина растет с увеличением времени ханения до двух суток и понижением температуры до 268 К.

Опыты с яичным меланжем тоже показали применимость реологических моделей Гершеля – Балкли и Оствальда де Вале, что еще раз подтверждает целесообразность использования этих малопараметрических эмпирических формул в реометрии пищевых материалов вместо громоздких общих интерполяционных формул.

2.4. Теория ротационных вискозиметров

Рассмотрим подробно теорию ротационных вискозиметров, поскольку в инструкциях приборов, как правило, не приводятся математические выкладки, из-за чего не всегда ясно, какие сделаны при выводе расчетных формул допущения, а в справочной литературе нередки опечатки. Кроме того, данное учебное пособие предусматривается как литература для учебных занятий, поэтому в нем нецелесообразно приводить конечные формулы с отсылкой на какую-либо справочную литературу.

Для конкретности рассмотрим схему ротационного вискозиметра типа немецкого вискозиметра «Реотест», в котором внешний цилиндр неподвижен, а внутренний вращается (на нем измеряются крутящий момент и угловая скорость). Схема прибора показана на рис. 2.3. Течение полагаем стационарным, ламинарным, изотермическим. Компоненты скорости течения вдоль продольной оси цилиндров и в направлении радиуса полагаем равными нулю. Следовательно, реологические эффекты второго порядка: эффекты Вейссенберга, Пойнтинга, вихри Тейлора – в рамках данной теории не описываются.

Рис. 2.3. Расчетная схема ротационного вискозиметра

Запишем уравнение равновесия в моментах относительно оси вращения мысленно выделенного цилиндрического осесимметричного элемента вискозиметра с ротором и слоем жидкости, на который действуют активный момент на роторе и реактивный момент от сил вязкого трения на внешней поверхности цилиндра жидкости:

2r²L – M_L = 0, (2.101)

где r – текущий радиус; L – длина цилиндров;  – касательное напряжение на поверхности цилиндра жидкости с радиусом r; M_L – крутящий момент, активный момент.

Тогда

(2.102)

где  – крутящий момент на единицу длины цилиндров; ₁, ₂ – касательное напряжение на рабочих поверхностях внутреннего и наружного цилиндров; r₁– наружный радиус внутреннего цилиндра (ротора); r₂ – внутренний радиус неподвижного наружного цилиндра.

Такой же результат можно получить из уравнений движения в цилиндрических координатах. Из кинематических соображений запишем скорость сдвига в жидкости в цилиндрических координатах:

, (2.103)

где  – скорость сдвига на поверхности цилиндра жидкости с текущим радиусом;  (r) – угловая скорость цилиндра жидкости с текущим радиусом; v (r) – линейная скорость точек цилиндра жидкости с текущим радиусом.

Реологическое уравнение жидкости с учетом выражений (2.102) можно записать следующим образом:

. (2.104)

Из этой записи следует, поскольку в уравнении отсутствует время, то эффекты тиксотропии и реопексии лежат вне данной теории, хотя в принципе ротационные вискозиметры достаточно удобные приборы для изучения этих реологических нестационарностей. С математической точки зрения важно, чтобы функция (2.104) была однозначной и удовлетворяла обычным условиям непрерывности и дифференцируемости, что автоматически обеспечивает физическая природа реологического уравнения.

Из уравнений (2.103) и (2.104) запишем

. (2.105)

Заметим, что при записи верхних пределов интегрирования полагают прилипаемость жидкости к поверхности неподвижного цилиндра вискозиметра v (r₂) = 0,  (r₂) = 0. Проведя интегрирование и поменяв местами пределы интегрирования, получим

. (2.106)

Продифференцируем первое уравнение из выражений (2.102) и немного его преобразуем:

. (2.107)

Тогда выражение (2.106) в новых переменных интегрирования в правой части, опять поменяв местами пределы интегрирования, можно переписать в виде

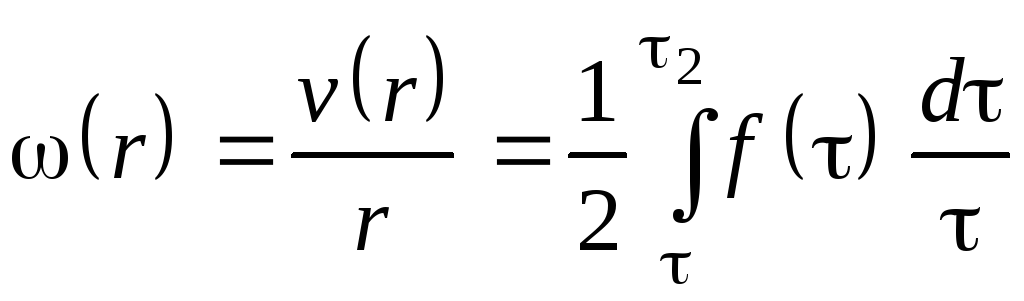. (2.108)

Чтобы связать напряжение с измеряемой на вискозиметре угловой скоростью ротора, примем текущий радиус за радиус ротора и запишем выражение (2.108) в виде

. (2.109)

Выведем самое распространенное в теории ротационных вискозиметров – формулу Маргулеса. Примем за реологическое уравнение линейное уравнение ньютоновской жидкости и проведем интегриро-вание правой части выражения (2.109):

(2.110)

.

Подставим в (2.110) величины касательных напряжений из формул (2.102) и получим формулу Маргулеса:

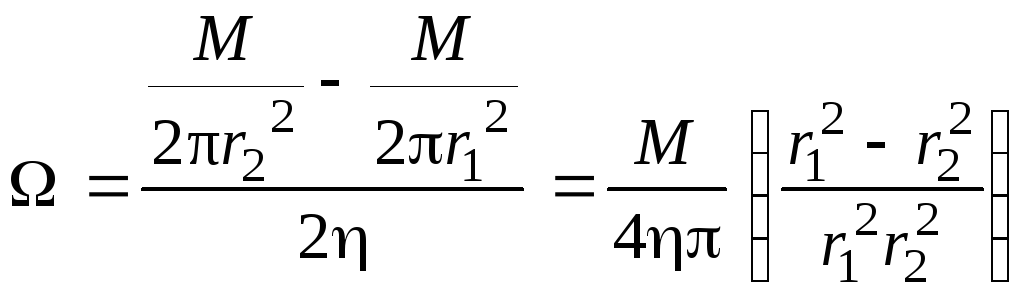. (2.111)

Следовательно, коэффициент динамической вязкости ньютоновской жидкости с аналитической точки зрения можно определить однократным измерением момента на роторе и угловой скорости его вращения:

. (2.112)

Повторные опыты нужно проводить лишь для получения статистических вероятностных показателей, на которые указывалось в начале данной главы. Поскольку момент и угловая скорость имеют разные знаки, коэффициент вязкости будет положительным. Формулу (2.112) можно использовать при вискозиметрировании таких текучих пищевых материалов, как, например, молоко, растительные масла и различные растворы и суспензии с малой концентрацией твердой фазы.

Если конструкция вискозиметра такова, что ротор вращается в условно-бесконечной среде жидкости, то нужно изменить краевые условия и проводить интегрирование по формуле (2.105) следующим образом:

. (2.113)

Далее аналогично (2.105)–(2.112) запишем

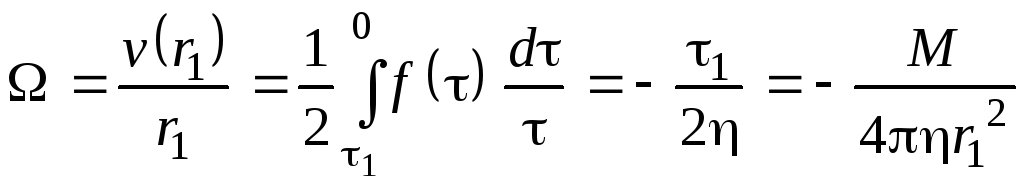(2.114)

или

. (2.115)

Этот же результат можно получить в пределе непосредственно из формулы (2.112):

. (2.116)

Иногда в формулах (2.112) и (2.116) приписывают сомножителем ускорение свободного падения, что не нужно делать, как легко установить из элементарного анализа размерностей в гостированной системе единиц СИ:

. (2.117)

В некоторых старых изданиях в качестве единицы измерения коэффициента внутреннего трения (вязкости) используется пуаз или сантипуаз, поэтому приведем связь между единицами:

(2.118)

Сомножитель, равный ускорению свободного падения, в формуле (2.112) появляется при переводе коэффициента вязкости из сантипуаз в единицы СИ [Пас].

Во многих конструкциях вискозиметров типа вискозиметра Куэтта внешний цилиндр вращается с угловой скоростью , а момент М измеряется на внутреннем неподвижном цилиндре с помощью тор-сионных измерительных систем, где момент является реактивным. В этом случае активный момент на внешнем цилиндре и угловая скорость совпадают по знаку. Приведем вывод формулы Маргулеса для данной конструкции, для чего выражение (2.105) перепишем в виде

. (2.119)

Далее, следуя выводу (2.105)–(2.112), запишем

; (2.120)

; (2.121)

. (2.122)

Подставим в (2.120) реологическое уравнение ньютоновской жидкости и определим распределение скоростей течения по радиусу:

;

. (2.123)

Из (2.122) получим угловую скорость:

. (2.124)

Откуда, аналогично (2.112), получим формулу Маргулеса для определения коэффициента динамической вязкости, с той только лишь разницей, что радиусы поменялись местами:

. (2.125)

В предыдущих решенных задачах на определенном этапе предполагали, что жидкость подчиняется реологическому уравнению Ньютона. В действительности при вискозиметрировании пищевых сред, особенно большой вязкости, это предположение не корректно. Мы не знаем вида реологического уравнения среды, а именно определение этого уравнения является целью ротационного вискозиметрирования, как и капиллярного вискозиметрирования, где эта проблема решалась с помощью уравнения Рабиновича.

Сформулируем задачу следующим образом: определить вид функции на ротационном вискозиметре, для определенности – типа вискозиметра Куэтта. Введем следующие обозначения, используя выражения (2.102):

. (2.126)

На основании (2.103) запишем

. (2.127)

Проведем интегрирование:

; (2.128)

. (2.129)

Дифференцируя (2.129) по ₁, как и при выводе уравнения Рабиновича, получим выражение вида

 . (2.130)

Однако выражение (2.130) не позволяет так просто, как формула (2.69), выразить скорости сдвига на стенке внешнего цилиндра. Из уравнения равновесия легко вычислить касательные напряжения, и дальнейшая прямая аналогия с теорией капиллярных вискозиметров исключается.

Уравнение (2.129) называется линейным интегральным уравнением типа Вольтерра. Применительно к ротационной вискозиметрии его решил в 1953 г. Павловский, который вывел следующее выражение для вычисления скоростей сдвига:

. (2.131)

Следовательно, получив технические кривые вискозиметрирования в координатах моментов и угловых скоростей, определив по формуле через моменты касательные напряжения на поверхности внутреннего цилиндра, по формуле Павловского можно рассчитать скорости сдвига на этой же поверхности и подобрать с помощью какого-либо метода, описанного в начале данной главы, подходящий вид эмпирического реологического уравнения.

Формула Павловского позволяет оценить погрешность, возникающую при ротационном вискозиметрировании, если коэффициент эффективной вязкости неньютоновской жидкости рассчитывать по формуле Маргулеса, что делается весьма часто. Между тем формула Маргулеса справедлива лишь для ньютоновских жидкостей.

Введем новый геометрический симплекс с, пусть вискозиметрируют степенную жидкость типа жидкости Оствальда де Вале, имеющую реологическое уравнение вида

(2.132)

Если рассчитывать эффективную скорость сдвига и эффективный коэффициент вязкости по формуле Маргулеса, то получим

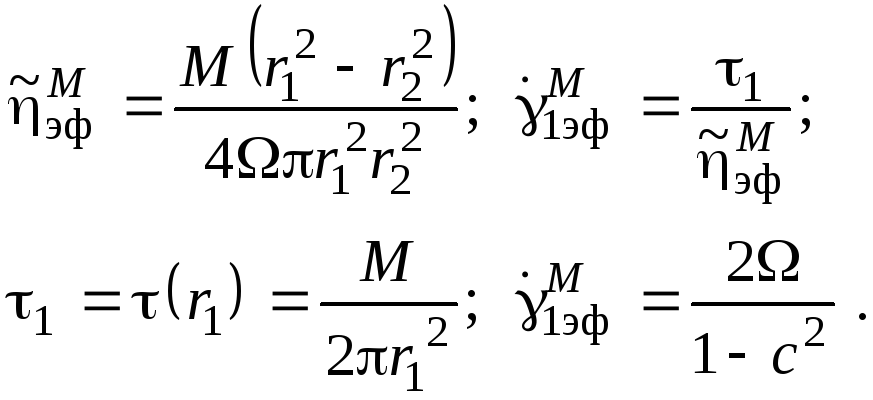
(2.133)

Вычислим по формуле (2.129) угловую скорость для степенной жидкости:

. (2.134)

Тогда по формулам (2.133) и (2.134) вычислим коэффициент эффективной вязкости:

. (2.135)

Формула (2.135) неточна, поскольку использовалась формула Маргулеса, она справедлива только для ньютоновской жидкости. Погрешность обусловлена неточностью расчета скорости сдвига на стенке внутреннего цилиндра. Рассчитаем эту скорость по формуле Павловского и сравним результаты по эффективному коэффициенту динамической вязкости:

. (2.136)

Расчет показывает, что при a = n = 0,5 погрешность равна 20 %. При n = 1, т. е. при ньютоновской жидкости, погрешность равна нулю.

Учитывая вышеизложенное, можно сделать вывод, что ротационная вискозиметрия требует проверки следующих требований, вытекающих из условий вывода предыдущих формул:

1. При вискозиметрии надо исключить концевые эффекты параллельными опытами на роторах разной длины и одного радиуса.

2. Обеспечить ламинарность течения.

3. Проверить отсутствие пристенного проскальзывания.

4. Проверить среду на тиксотропию и реопексию.

5. Для жидкостей с ньютоновской вязкостью можно использовать формулу Маргулеса, для неньютоновских жидкостей при обработке данных вискозиметрирования надо использовать формулу Павловского.