1.8. Вязкоупругость

Гуковское линейно-упругое твердое тело и ньютоновская линейно-вязкая жидкость в некотором смысле представляют собой две крайние модели линейных тел. между тем многие пищевые среды в деформационных процессах проявляют одновременно упругие и вязкостные свойства. Такие пищевые среды называются вязкоупругими. Для них можно построить ряд промежуточных моделей.

Одной из простейших вязкоупругих моделей является механическая модель тела или жидкости Максвелла, которая представляет собой последовательное соединение тел Гука и Ньютона. Символьная формула модели имеет вид М = N – Н.

Математическая модель Максвелла строится в предположении, что деформация (пусть для определенности это будет деформация простого сдвига) в некоторой точке среды представляет собой сумму упругой деформации и деформации течения, инерционными эффектами можно пренебречь:

, (1.92)

где  – общая деформация сдвига; _H – упругая деформация тела Гука; _N – деформация течения тела Ньютона.

Из реологических уравнений тел Гука и Ньютона запишем

, (1.93)

где  – коэффициент динамической вязкости; G – модуль сдвига (модуль упругости второго рода).

Продифференцируем уравнение (1.92) по времени и подставим выражения (1.93):

(1.94)

Последнее уравнение (1.94) называется реологическим уравнением тела Максвелла. С помощью этого уравнения, например, можно проанализировать процесс релаксации напряжений в среде при постоянной деформации:

. (1.95)

Решение дифференциального уравнения (1.94) имеет следующий вид:

, (1.96)

откуда

. (1.97)

Константу интегрирования С находим из условия, что в начальный момент времени известно начальное напряжение t₀:

. (1.98)

Тогда процесс релаксации напряжений при постоянной деформации описывается уравнением

. (1.99)

С течением времени в теле Максвелла при постоянной деформации напряжение экспоненциально стремится к нулю:

. (1.100)

Заметим также, что отношение динамической вязкости к модулю упругости имеет размер времени. Тогда

; (1.101)

. (1.102)

З а время t₁ начальное напряжение уменьшается на 37 %. Это время иногда называют временем релаксации (рис. 1.8).

Рис. 1.8. Кривая релаксации напряжений

С позиции наглядной механической модели эта математическая модель представляет собой последовательное соединение пружины (тело Гука) и демпфера (жидкость Ньютона). Если соединить пружину и демпфер параллельно, то получим наглядную модель тела Кельвина – Фойгта. Реологическое уравнение тела Кельвина – Фойгта получим в предположении, что в некоторой точке среды общее напряжение состоит из суммы напряжения за счет упругости среды и напряжения за счет вязкости жидкости:

 = _N + _Н; (1.103)

 = . (1.104)

Уравнение (1.104) является реологическим уравнением Кельвина – Фойгта, с помощью которого можно изучить процесс ползучести дисперсной среды при постоянных напряжениях.

В теории вязкоупругости находят широкое применение интегральные уравнения Вольтерры, которые позволяют удобным образом связать математически процессы релаксации напряжений и ползучести деформаций.

Общий нелинейный закон наследственной ползучести при одноосном напряженном состоянии предложил Ржаницын:







 

, (1.105)

где  – деформация; t – момент времени, в который определяется деформация;  – текущее время, переменная интегрирования;  – напряжение; K – ядро интегрального уравнения.

Более простые выражения, как частные случаи уравнения (1.105), предложили Лидерман и Разовский:

, (1.106)

где Е – мгновенный модуль упругости;

Арутюнян:

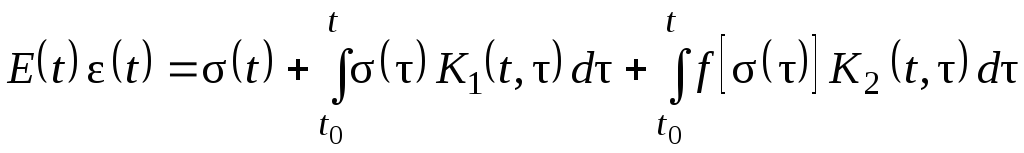; (1.107)

Вульфсон:

; (1.108)

Работнов:

. (1.109)

Этими уравнениями описывалась ползучесть разнообразных материалов: полимеров, бетона, металлов. Если нет явной необходимости использовать более сложные интегральные уравнения, то для описания вязкоупругих свойств пищевых материалов можно использовать теорию линейно-наследственной ползучести, согласно которой закон деформирования материала можно записать в виде уравнения

, (1.110)

ядро которого можно просто определить испытаниями на ползучесть при постоянных напряжениях.

Математически ядро уравнения (1.110) часто представляют в виде линейной комбинации экспоненциальных функций:

. (1.111)

Тогда простейшее ядро имеет вид

. (1.112)

В некоторых случаях можно использовать ядро Дюффинга

(1.113)

или его частный случай – ядро Больцмана

. (1.114)

Для описания процесса релаксации напряжений можно уравнение (1.110) с помощью преобразования Лапласа привести к виду

, (1.115)

где R (t – ) – ядро интегрального уравнения (1.115), являющееся резольвентой интегрального уравнения (1.110).

Подставим напряжение из уравнения (1.115) в уравнение (1.110):

, (1.116)

откуда

=

. (1.117)

Следуя выводу Ржаницына, запишем уравнение (1.117) в виде

. (1.118)

Учитывая, что   0, R()  0,

(1.119)

или

. (1.120)

Для разрешения интегрального уравнения относительно ядра релаксации напряжений опять воспользуемся методами операционного исчисления. Поскольку эти методы широко используются также при решении дифференциальных уравнений, приведем минимальные, основные сведения об операционном исчислении, достаточные для уяснения идеи операционного исчисления и необходимые для преобразований в дальнейшем.

В операционном исчислении оригинал функции переводят в его изображение с помощью преобразования Лапласа:

, (1.121)

где  – изображение; p – параметр;  – оригинал функции.

С помощью преобразования Лапласа можно доказать следующие простейшие свойства, которые будут использованы в дальнейшем:

;

;

; (1.122)

.

Пользуясь выражениями (1.122), применим преобразование Лапласа к правой и левой частям интегрального уравнения (1.119):

, (1.123)

откуда

. (1.124)

Применив к формуле (1.124) обращение изображения, получим искомый оригинал резольвенты интегрального уравнения R (t – ) . Например, пусть ядро интегрального уравнения линейной наследственной ползучести выражено через экспоненциальную функцию, совершим преобразование этого оригинала:

. (1.125)

Согласно формуле (1.124), получим изображение ядра резольвенты и совершим обращение изображения, пользуясь свойствами преобразования Лапласа (1.122):

. (1.126)

Тогда процессы деформации и изменения напряжений, согласно формулам (1.110) и (1.115), можно описать выражениями

; (1.127)

. (1.128)

Данные выражения позволяют предложить простой способ определения ядра интегрального уравнения (1.110) из опытов на ползучесть при постоянном напряжении. Пусть материал перед опытом находится в естественном начальном состоянии, которое в дальнейшем не вызывает в нем никаких изменений, что математически можно выразить следующим образом:

. (1.129)

Тогда уравнение (1.110) перепишем для следующего условия: то, что до опыта было равно нулю, в нулевой момент отсчета времени изменилось от нулевого напряжения до какого-то значения ₀ и затем поддерживалось при этой постоянной величине:

. (1.130)

Измерив непосредственно после приложения напряжений начальную деформацию, можно вычислить модуль Е:

. (1.131)

Продифференцируем уравнение (1.131) по времени и получим выражение для ядра интегрального уравнения:

. (1.132)

Изложенный подход использования интегральных уравнений применили А. Д. Дорогин, Л. Е. Мальцев и В. И. Кучерюк  при исследовании вязкоупругих свойств аортального клапана сердца человека. Авторы наблюдали нелинейную ползучесть, однако кривые ползучести были удовлетворительным образом подобны, поэтому опыты описывались аналитически в квазилинейной форме:

. (1.133)

Ядро уравнения принято в виде ядра Ржаницына – Колтунова

; , (1.134)

что справедливо для времени 0  t  0,5.

Были найдены коэффициенты а = 0,280; А = 0,0274; b = 0,166; = 79,3 кгс/см² и получено уравнение релаксации для линейной области, тоже в виде интегрального уравнения типа уравнения Вольтерры.

Следует отметить, что в реологии вязкоупругость очень часто моделируется с помощью дифференциальных уравнений, составляемых на базе символьных формул и наглядных механических моделей, многие из которых имеют общепринятые названия по фамилиям авторов: модели Максвелла, Кельвина – Фойгта, Пойнтинга – Томсона, Шофильда – Скотт-Блэра и др. Однако период развития реологии, когда изобретали все новые, более сложные механические модели, прошел, так же как и период изобретения математических моделей неньютоновских жидкостей. Современный математический аппарат предлагает для решения проблем деформаций и течения общие подходы, а вычислительные трудности стали более легко преодолимыми с распространением мощных персональных компьютеров. Тем не менее механические модели полезны в силу своей наглядности и качественной сопоставимости с решениями многих проблем вязкоупругости с помощью дифференциальных уравнений, как было показано на примере модели Максвелла.

Распространенность такого механического и математического моделирования демонстрирует работа Ю. В. Маковецкого, Ю. Н. Смо-лина  и Г. А. Чуича, которые исследовали механические свойства печени методом деформации сжатием. Была использована модель Куна, состоящая из двух вязкоупругих элементов Максвелла, соединенных параллельно:

;

; (1.135)

,

где  – общее напряжение в системе; ₁, ₂ – напряжения, полученные экстраполяцией к нулевому времени двух условно прямолинейных участков полулогарифмических графиков ln  – t; t – время релаксации; E и E₁, E₂ – общий и релаксационные модули упругости.

Однако в диапазоне относительных деформаций 0,29 – 0,73 модель не работает. Были получены эмпирические нелинейные зависимости для модулей упругости и вязкости первого демпфера:

; (1.136)

А₁ = 1990; А₂ = 2300; В₁ = 9; q₁ = 7; q₂ = 5,2; k = 14;

₁ = ₁ = ; (1.137)

время релаксации ₂ почти не зависит от деформации и равно 22,6 с;

. (1.138)

Символьная формализация достаточно удобна для составления этих дифференциальных уравнений, поэтому полезно будет рассмотреть механическое и символьное моделирование вязкоупругих свойств типовых материалов немного подробнее.