2.4.Переходные функции( временные характеристики) элементов сау

Переходная функция элемента или звена САУ представляет собой график изменения во времени выходной величины эвена, вызванно­го подачей на его вход единичного ступенчатого воздействии. Аналитиче­ское выражение для переходной функции обозначают h(t). При подаче на вход ступенчатого воздействия x_вх=const в системе или звене будет возникать переходный процесс х_вых=f(t).Одним из способов получения кривой переходного процесса является использование обратного преобразования Лапласа, в соответствии с которым оригинал функции х_вых может быть получен в соответствии со следующим выражением

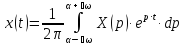. (2.20)

Переходная функция системы h(t) может быть получена с использо­ванием её передаточной функции, записанной в виде

,

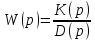где К(р) - полином числителя передаточной функции;

D(p) - полином знаменателя передаточной функции.

Используя обратное преобразование Лапласа (2.20), можно получить следующее выражение для переходной функции:

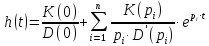, (2.21)

где p_i - корни характеристического уравнения системы;

К(0) и D(0) - полиномы передаточной функции для установившегося режима работы системы (р=0);

K(p_i), D(p_i) - выражения для полиномов передаточной функции при p=p_i;

D'(p_i) — производная полинома знаменателя.

Переходные процессы x_вых=f(t), описываемые переходными функциями, крайне разнообразны.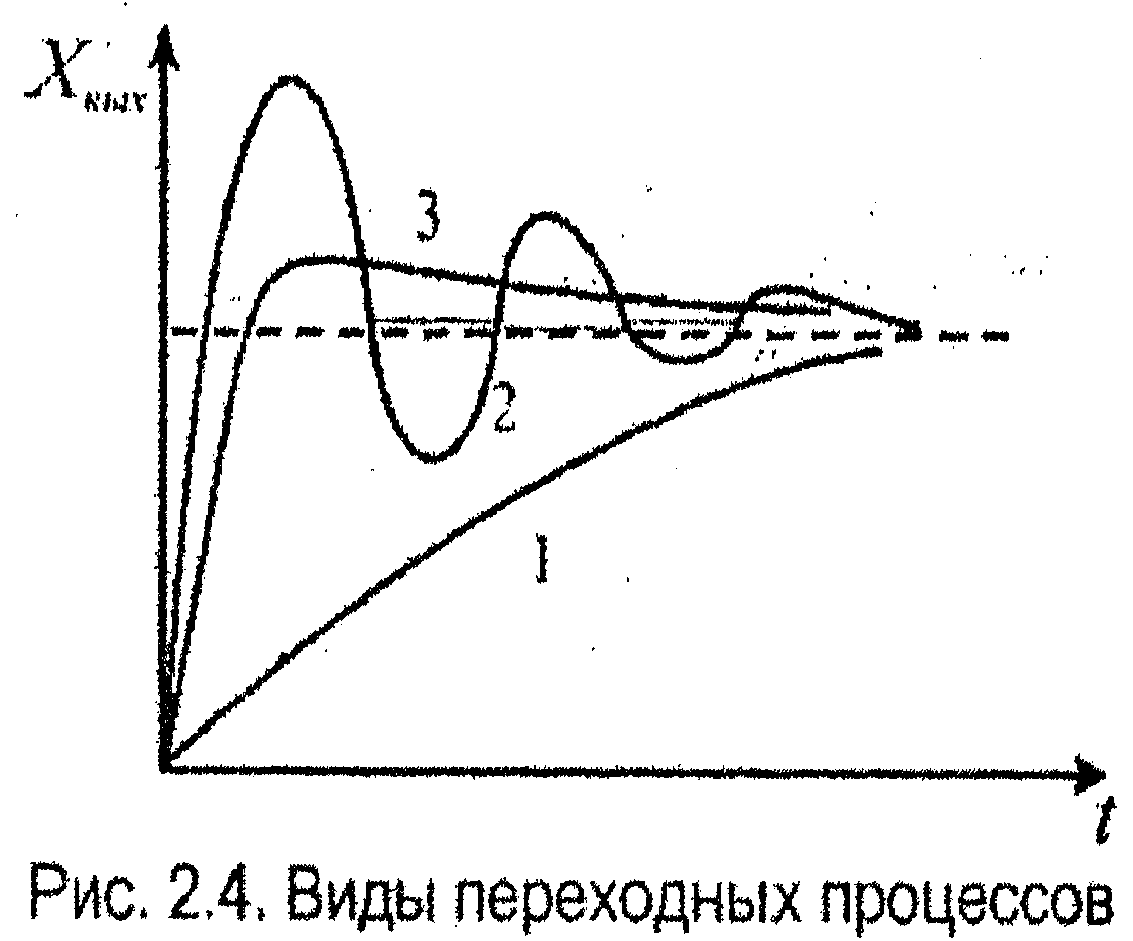

Их можно разбить на 3 основных

вида (рис. 2.4):

1) монотонные, в которых первая произ­водная выходной величины не меня­ет знак;

2) колебательные периодические, в ко­торых производная меняет знак тео­ретически бесконечное число раз;

3) апериодические, протекающие без периодичности смены знака производной и имеющие ограниченное число экстремумов.

2.5.Импульсная переходная(весовая)

ФУНКЦИЯ ЗВЕНА

Импульсная переходная функция есть реакция эвена на еди­ничный импульс δ(t) (мгновенный импульс с бесконечно большой ампли­тудой и единичной площадью). Она обозначается как ω(t).

Выражение для единичного импульса соответственно называется единичной импульсной функцией или дельта-функцией и обозначается δ(t). Следовательно, весовая функция ω(t) является изменением выход­ной величины при подаче на вход сигнала x(t)=δ (t).

Математически δ-функция может быть записана следующим образом:

.

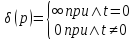При этом согласно определению

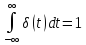. (2.22)

Дельта-функция может быть получена дифференцированием единич­ного скачка, т.е.

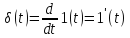. (2.23)

Отсюда следует аналогичная связь между переходной и весовой функ­циями линейных звеньев

, (2.24)

т.е. весовая функция есть производная от переходной функции.

И наоборот

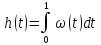. (2.25)

2.6.Частотные характеристики сау

Рассмотрим понятие о частотных характеристиках, которые широко используются при анализе САУ. Это понятие применимо как к от­дельному звену, так и к системе в целом. Частотные характеристики опи­сывают установившиеся вынужденные колебания на выходе звена, вы­званные гармоническим воздействием на входе. Рассмотрим такой режим.

Пусть на вход линейной разомкнутой системы, изображенной на рис. 2.5, подано гармоническое воздействие

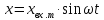, (2.26)

или в символической форме

, (2.27)

где x_вх.m –амплитуда;

ω- угловая частота этого воздействия.

По истечении некоторого времени после подачи такого воздействия, после окончания переходного процесса, на выходе системы установится также гармоническое изменение выходной величины, но с другими амплитудой и фазой (рис.2.6).

Следовательно, в установившемся режиме выходная величина сис­темы будет

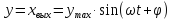, (2.28)

. (2.29)

При фиксированной амплитуде входных колебаний амплитуда и фаза установившихся колебаний на выходе системы зависят от частоты вход­ного возмущающего воздействия. Если постепенно увеличивать от нуля частоту колебаний и определять установившиеся значения амплитуды и фазы выходных колебаний для разных частот, то можно получить зависимости от частоты отношения амплитуд 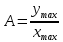и сдвига фаз φ(ω) выходных и входных установившихся колебаний. Эти зависимости назы­ваются соответственно A(ω) — амплитудной частотной характеристикой

(АЧХ) и φ(ω) - фазовой частотной характеристикой (ФЧХ).

Рассмотрим основные понятия, связанные с частотными характери­стиками.

Пусть задана система дифференциальных уравнений какой-либо ра­зомкнутой системы n-го порядка. Операторные уравнения этой системы

имеют следующий вид:

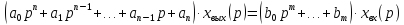(2.30)

Если подать на вход этой системы гармоническое возмущение

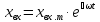, (2.31)

то на выходе будем иметь

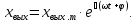(2.32)

Известно, что

.

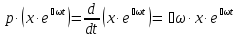Аналогично

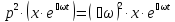
и т,д. Поэтому операторные уравнения для разомкнутой системы записать в виде

/им

. (2.33)

Сокращая на е^ϳωt, получим выражение, которое позволяет определить при заданном периодическом возмущении на входе изменение амплитуды

и фазы на выходе системы (звена) в зависимости от частоты ω.

. (2.34)

Это выражение представляет собой передаточную функцию звена или

разомкнутой системы, в которой вместо p подставлено (ϳω), т.е.

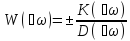. (2.35)

Выражение W(ϳω) называют комплексным коэффициентом передачи (усиления) или комплексной частотной функцией разомкнутой системы. При ω=0 получим выражение для коэффициента передачи системы.

Эту функцию можно представить в декартовых координатах на ком­плексной плоскости

, (2.36)

где Р(ω) и Q(ω) - вещественная и мнимая части частотной передаточной

функции.

Или в полярных координатах

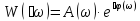. (2.37)

Отсюда имеем для АЧХ и ФЧХ

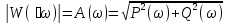, (2.38)

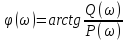. (2.39)

Модуль частотной передаточ­ной функции A(ω) может быть так­же найден как отношение модулей числителя и знаменателя характе­ристики W(ϳω). Фаза частотной пе­редаточной функции находится как разность аргументов числителя и знаменателя.

При некотором фиксированном значении частоты ω входного сигна­ла комплексная частотная функция W(ϳω) будет представлять собой вектор с амплитудой A(ω) и аргументом φ(ω) (рис.2.7). Для различных ω будут различные A(ω) и φ(ω). Если изменять ω от 0 до бесконечности, можно получить множество различных векторов. Огибающая, проведенная через концы этих векторов, называется годографом вектора комплексной частот­ной характеристики. Кривая называется также амплитудно-фазовой час­тотной характеристикой (АФЧХ). Иногда выражение, соответствующее W(ϳω), называют частотной передаточной функцией.

Следовательно, АФЧХ называется линия, соединяющая концы радиу­сов-векторов, длины которых равны отношению амплитуд выходного и входного сигналов, а угол, образуемый вектором с положительным на­правлением вещественной оси, равен разности фаз выходного и входного сигналов для частот, изменяющихся от 0 до ∞.

Примерный вид частотных характеристик можно представить на рис. 2.8.

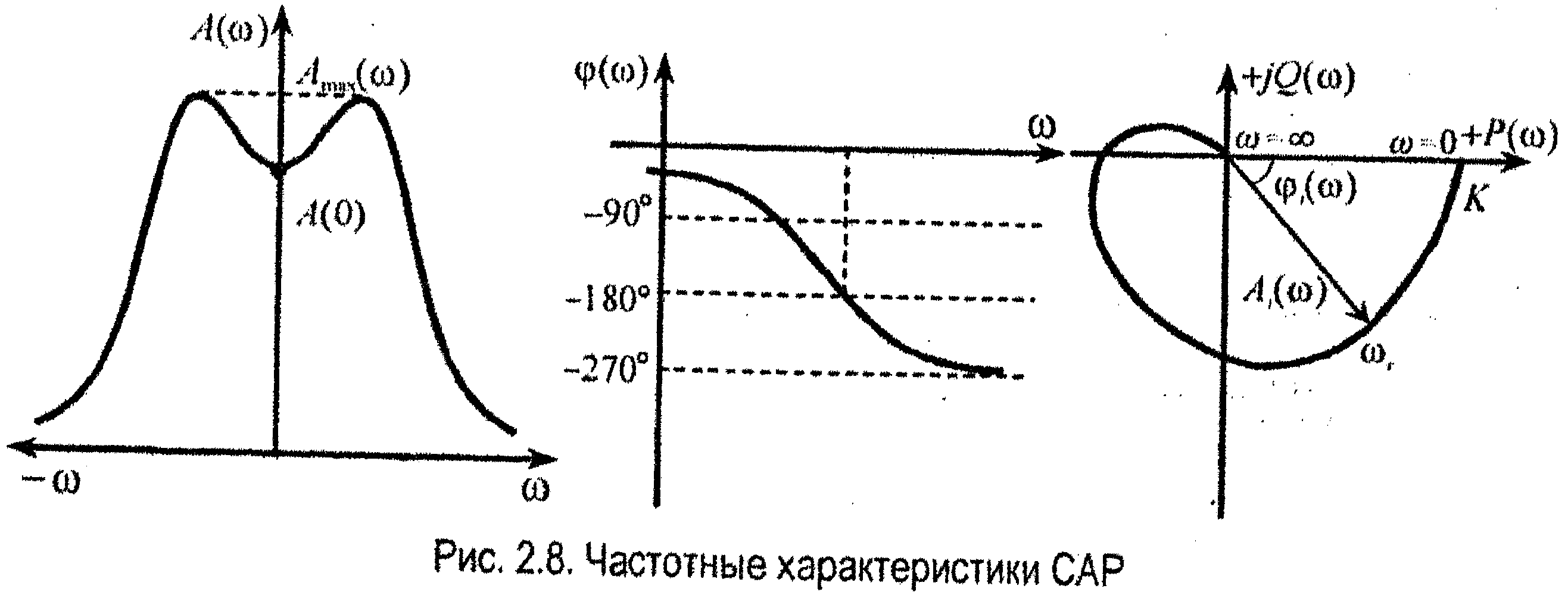
В соответствии с преобразованием Фурье АФЧХ должна строиться при изменении частот от -∞ до +∞.Но ветвь характеристики, получающаяся при изменении частот от 0 до -∞, можно получить как зеркальное отображение W(ϳω) относительно вещественной оси W(ϳω), полученной при изменении ω от +∞ до 0. Поэтому при характеристических расчетах достаточно ограничиться только положительными значениями ω.

Между переходной функцией и АФЧХ динамической системы также

существует определенная связь, т.к. они получаются из одного и того же дифференциального уравнения. В первом случае на вход подается воздействие типа единичного скачка, во втором случае - синусоидальное воздействие. Эта связь дает возможность по АФХ системы построить её переходную функцию, не решая уравнения. Для этого обычно использует­ся вещественная часть частотной АФХ. По графику переходной функции можно получить кривую переходного процесса при ступенчатом воздейст­вии, умножив все координаты переходной функции на входную величину.

По имеющейся переходной функции, полученной, например, экспери­ментальным путем, можно построить АФХ. Это обычно делается при авто­матизации сложных технологических объектов, у которых расчетным путем нельзя получить ни переходную функцию, ни частотные характеристики.