5.5. Апериодическое (инерционное) звено второго порядка

Исходное дифференциальное уравнение

.

Примерами этих звеньев являются двигатель постоянного тока, если на вход его подают напряжение, а выходом является его скорость; цепоч­ка R-L-C; генератор постоянного тока.

Операторное уравнение

.

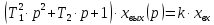Передаточная функция

.

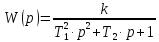Апериодическое звено 2-го порядка будет иметь место при последо­вательном соединении двух апериодических звеньев первого порядка ли­бо при колебательном звене, если Т₂>2Т₁ т.к. при этом корни характери­стического уравнения вещественные.

.

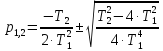В этом случае исходное дифференциальное уравнение примет вид

.

Корни характеристического уравнения

;

.

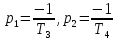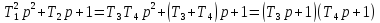Передаточная функция звена принимает вид

.

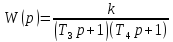Временные характеристики звена

Если характеристическое уравнение не имеет кратных и нуле­вых корней, переходная функция h(t) определяется с помощью обратного преобразования Лапласа. Если передаточную функцию представить в виде ,

то в соответствии с обратным преобразованием Лапласа

.

Для рассматриваемого звена i=2.

Корни характеристического уравнения

;

;

.

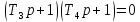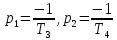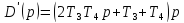Следовательно

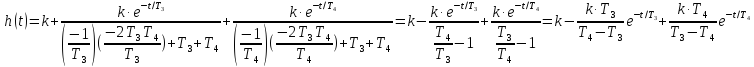(3.37)

или

(3.38)

При T₃>T₄.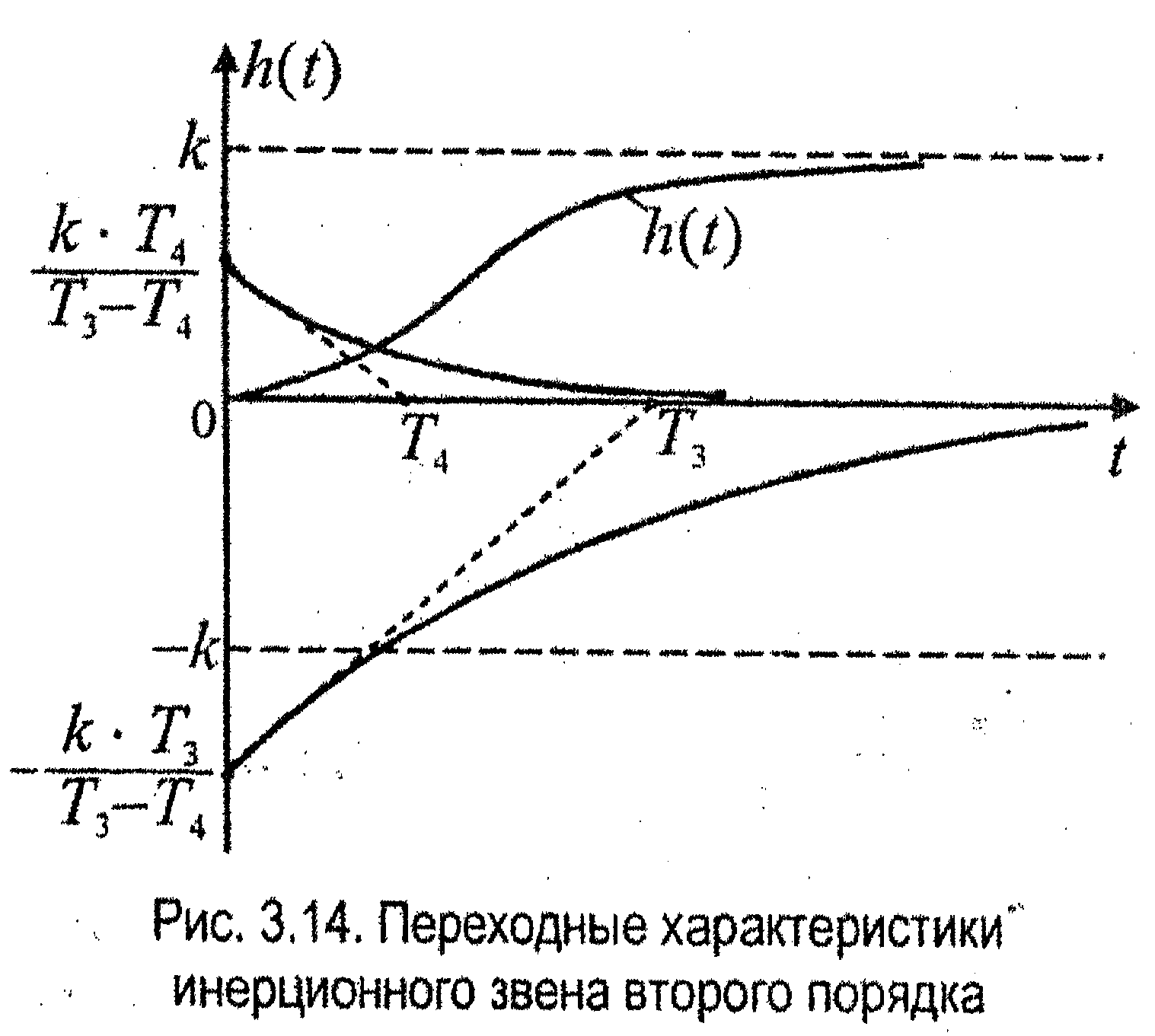

На рис. 3.14 представлены кривые переходного процесса инерционного звена 2-го порядка (его составляющие). Из графиков видно, что меньшие (малые) постоянные времени влияют на начало переходно­го процесса, а большие по­стоянные времени определя­ют среднюю часть и оконча­ние процесса.

Время переходного про­цесса (регулирования) может быть определено

.

Импульсная (весовая) пе­реходная функция (рис. 3.15)

.

Частотные характеристики звена

АФЧХ инерционного звена 2-го порядка имеет вид (рис. 3.16)

.

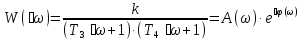Амплитудно-частотная характеристика А(ω) (рис. 3,17).

.

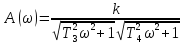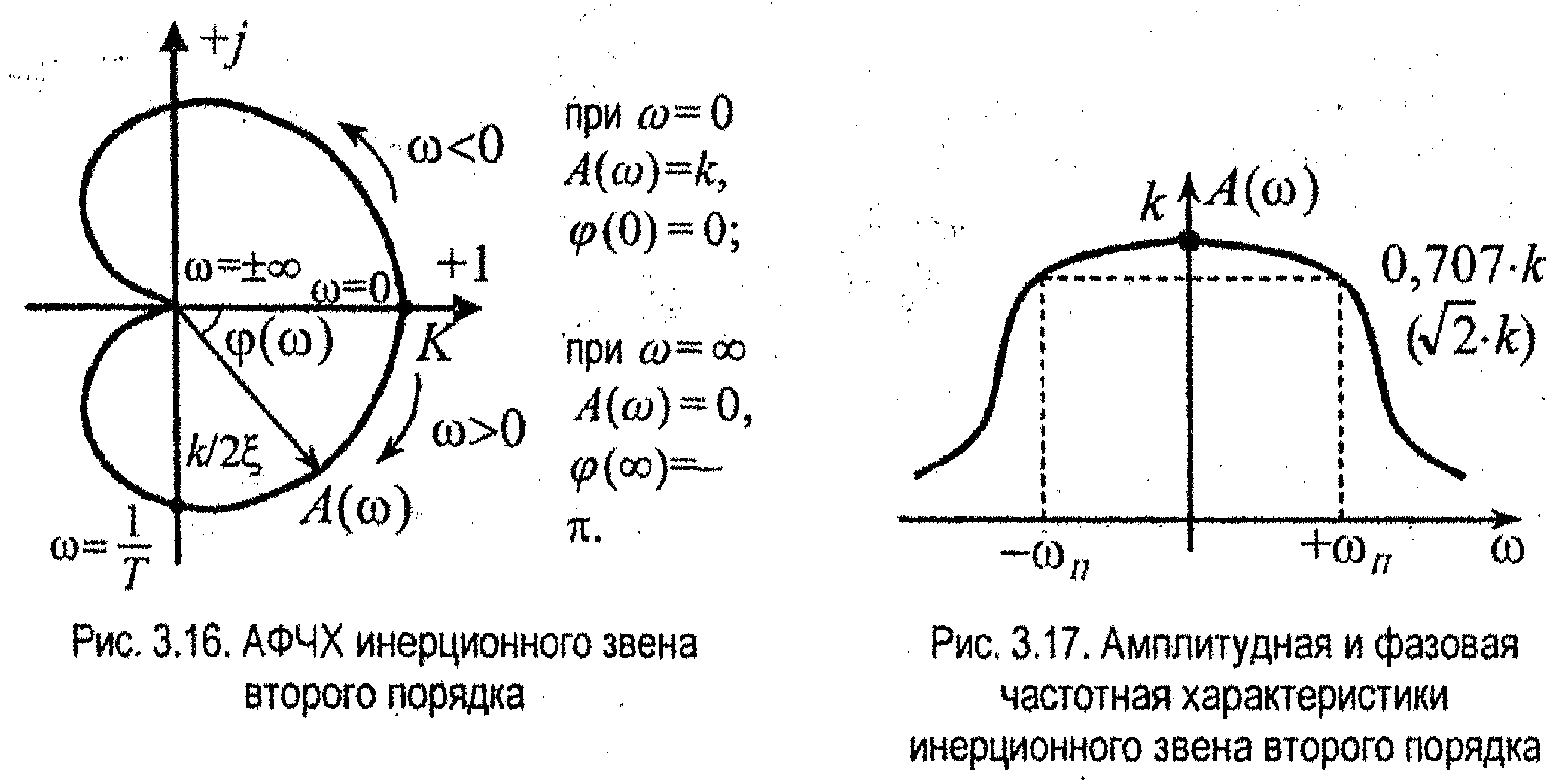
Фазочастотная характеристика φ(ω) (рис. 3.17)

.

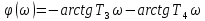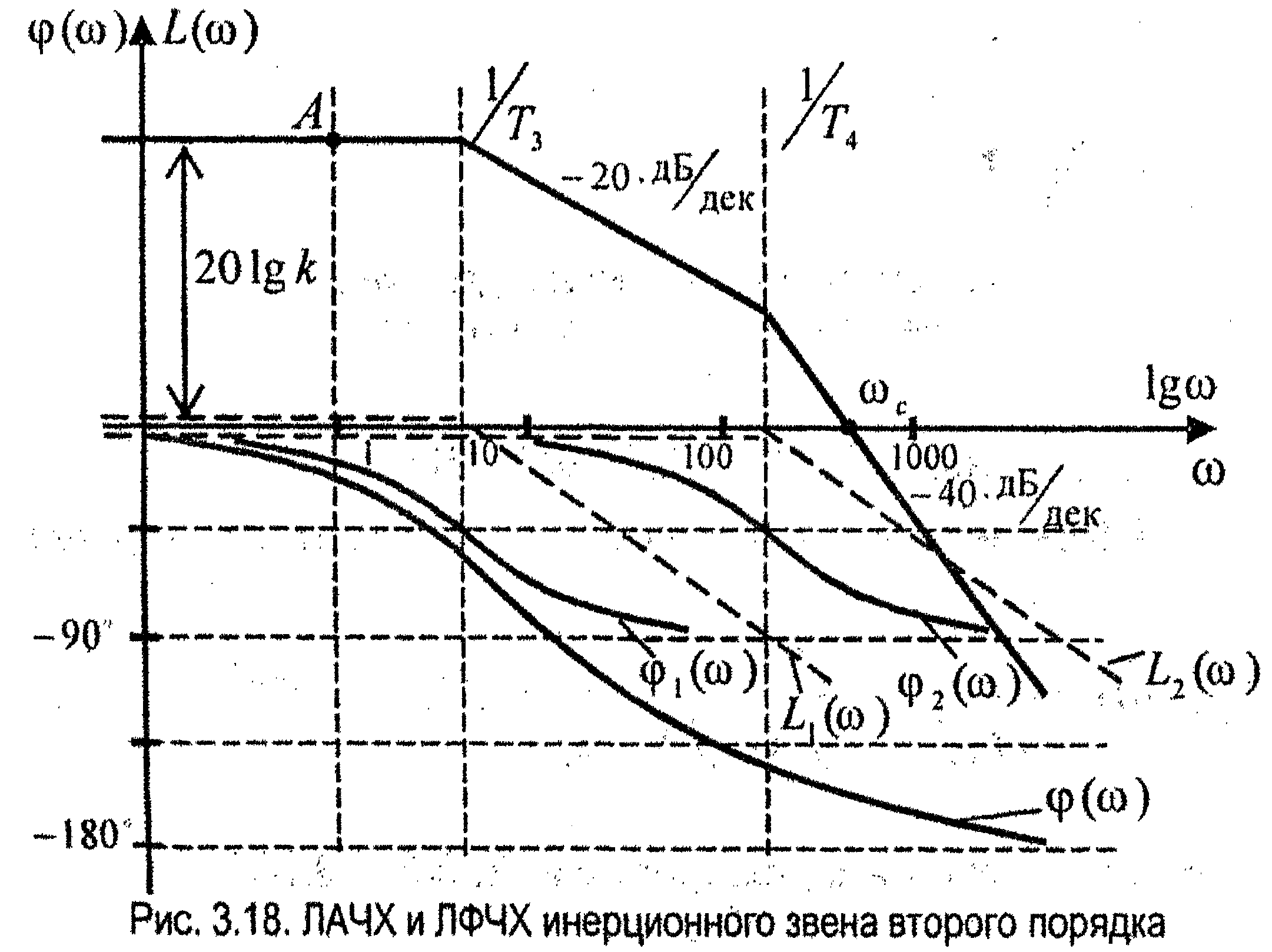
Логарифмические амплитуды L(ω) и фазовой φ(ω) частотные харак­теристики инерционного звена второго порядка представлены на рис. 3.18.

5.6. Консервативное звено

Консервативное звено может быть получено из колебатель­ного звена при ξ=0. Исходным уравнением консервативного звена будет

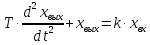. (3.39)

Данное звено является генератором гармонических синусоидальных колебаний.

Операторное уравнение звена

. (3.40)

Передаточная функция звена

. (3.41)

Структурная схема звена.

Переходная функция звеня h(t)

Характеристическое уравнение звена

.

Отсюда корни уравнения определяются

,

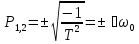Где 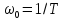- угловая частота колебаний.

.

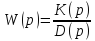Используя обратное преобразование Лапласа, получим следующие выражения для переходной функции:

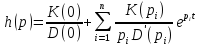. (3.42)

.

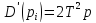Следовательно

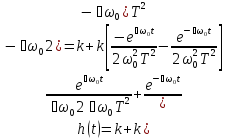. (3.43)

Или окончательно (рис. 3.19, a)

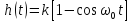, (3.44)

где .

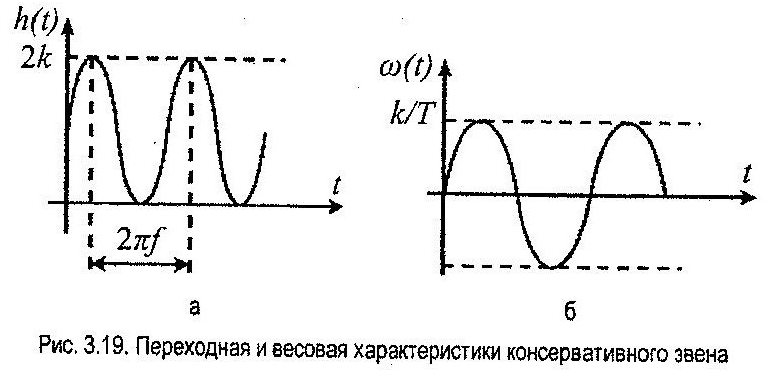
Весовая функция звена (рис. 3.19, б)

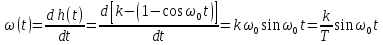. (3.45)

Частотные характеристики звена

Частотная комплексная передаточная функция

. (3.46)

Амплитудная частотная характеристика

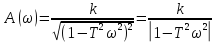. (3.47)

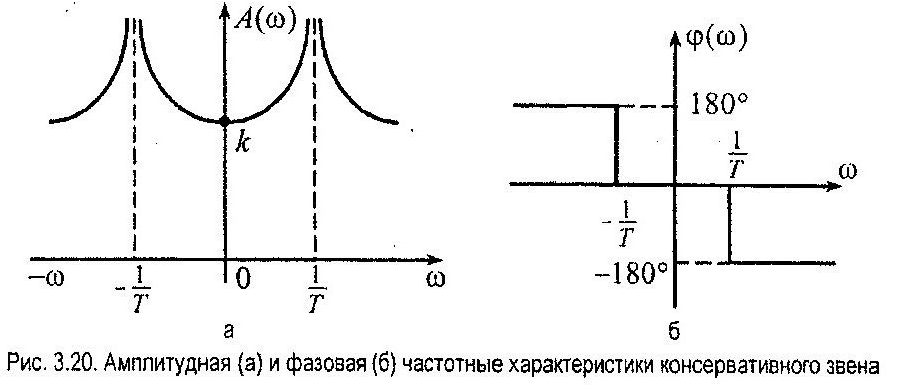
Амплитудная и фазовая частотные характеристики звена (АФЧХ) бу­дут иметь вид (рис. 3.20):

;

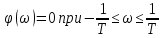; (3.48)

;

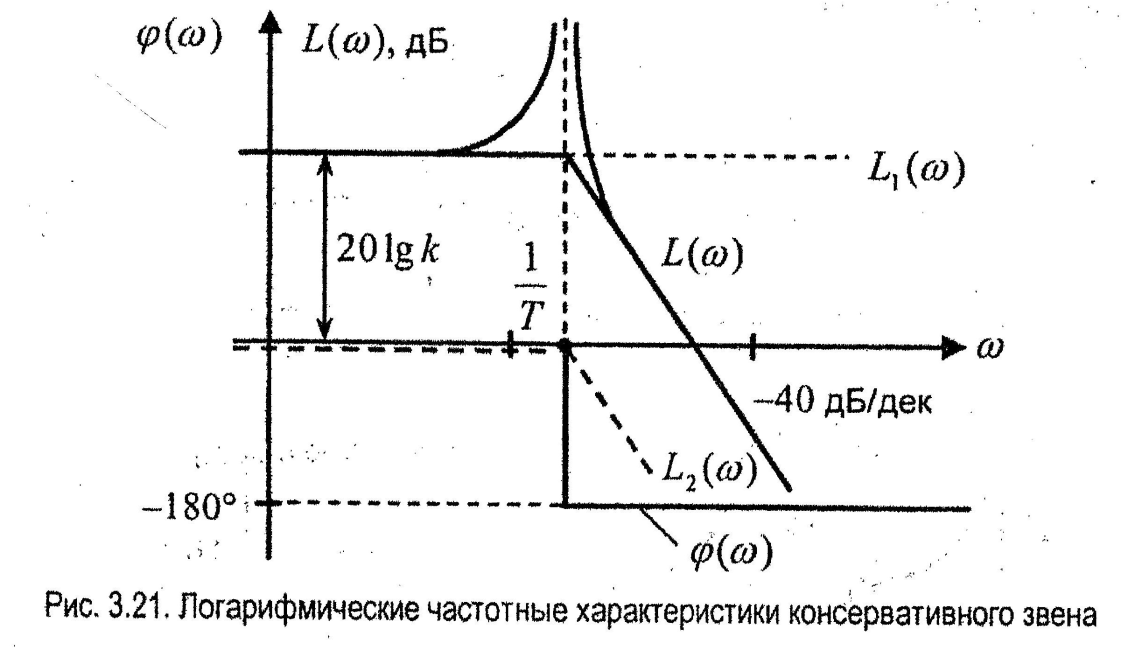
Логарифмические характеристики:

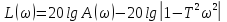; (3.49)

.

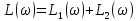Если ,

.

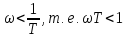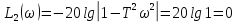Если ,

.

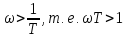Суммарная ЛАЧХ консервативного звена представлена на (рис. 3.21).