2.2. Математическое описание линейных сау

При исследовании динамических процессов в САУ использу­ются линейные дифференциальные уравнения. Дифференциальные урав­нения описывают связь между входным и выходным параметрами отдельных элементов и выражают аналитически характер изменения во времени выходного параметра при определенном виде входного параметра.

Предположим, что линейная САУ описывается дифференциальным уравнением п-го порядка с постоянными коэффициентами и это уравне­ние имеет следующий вид:

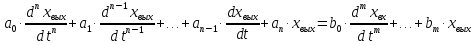, (2.1)

где х_вых = у - выходная величина звена (системы);

х_вх - входная величина эвена (в отклонениях от состояния равновесия);

a₁,a₂,….a_n-1,a_n,b₁,b₂,….b_n - постоянные коэффициенты, оп­ределяющие параметры звена.

При записи дифференциального уравнения члены, содержащие вы­ходную величину и её производные, записывают в левой части уравнений, а все остальные члены - в правой.

В принципе можно решить это уравнение и найти ответ, т.е. реак­цию системы y=x_вых(t) на входное воздействие u(t)=x_вх(t).Уравнение (2.1) описывает не только переходные, но и установившиеся процессы в системе.

Для определения связи между установившимся значением выходной величины x_вых и установившимся значением входной величины x_вх достаточно

приравнять к нулю все производные входной и выходной величины,

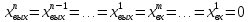. (2.2)

В этом случае дифференциальное уравнение упростится и даст иско­мую зависимость между х_вых и х_вх в установившемся режиме.

(2.3)

Разрешив это уравнение относительно х_вых._у1 получим статическую ха­рактеристику системы.

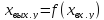. (2.4)

Запись уравнения в форме (2.1) неудобна, особенно, когда возникает не­обходимость исследовать взаимодействие отдельных звеньев системы при их соединении в различные цепи. Кроме того, решение уравнений с порядком выше третьего значительно усложняется и требует применения вычисли­тельной техники. Поэтому для упрощения решения уравнения (2.1) использу­ют средства описания динамических свойств системы через преобразование Лапласа. Основанием для этого служит то обстоятельство, что такое преоб­разование существенно облегчает исследование сложных систем, поскольку дифференциальные уравнения заменяются алгебраическими.

Преобразование Лапласа позволяет легко учитывать начальные усло­вия и избежать сложных выкладок при вычислении постоянных интегриро­вания. Преобразование Лапласа преобразует функцию вещественного переменного (в том числе времени) в функцию комплексного переменного.

Если имеется некоторая функция f(t) независимой переменной t, то преобразование Лапласа, производимое над функцией f(t) и обращающее её в функцию F(p), определяется соотношением

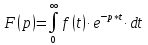, (2.5)

где p=α+ϳ∙ω - произвольная комплексная величина.

Функция f(t) называется оригиналом, а функция F(p) - изображени­ем функции f(t). При применении преобразования Лапласа к функции f(t) рассматриваются значения этой функции лишь при t>0, т.е. после прило­жения в системе внешних возмущающих воздействий, что характерно техническим задачам САУ.

Основные преобразования Лапласа были рассмотрены в других кур­сах, поэтому они здесь не рассматриваются.

Наряду с прямым преобразованием (2.5) функции времени f(t) в F(p), т.е. наряду с операцией перехода от функции вещественного переменного t к функции комплексного переменного p, пользуются обратным преобразова­нием, т.е. преобразованием изображения функции F(p) в оригинал f(t).

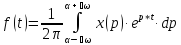. (2.6)

Преобразование Лапласа для типовых математических операций, а также для функций, часто встречающихся в задачах автоматического регулирования, можно найти в учебниках [1].

Пользуясь преобразованием Лапласа, представим дифференциаль­ное уравнение (2.1) в операторном виде.

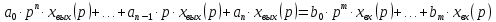
или

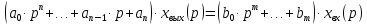, (2.7)

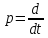где - оператор дифференцирования.

Последнее выражение является Лапласовым изображением дифференциального уравнения (2.1) при нулевых начальных условиях. Нулевые начальные условия состоят в том, что в системе n-го порядка при t>0 вы­ходная величина и все ее производные от первого до n-1 равны нулям.