3.4. Колебательное звено

Колебательным называется звено второго порядка, в котором при получении на входе ступенчатого воздействия, выходная величи­на стремится к новому установившемуся значению, совершая затухающие колебания.

Переходный процесс такого звена описывается дифференциальным уравнением второго порядка.

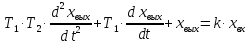(3.19)

или

(3.20)

где T₁ и Т₂ - постоянные времени колебательного звена, имеющие раз­мерность времени;

- коэффициент усиления (передачи) звена;

Т- эквивалентная постоянная времени звена ;

ξ - постоянная безразмерная величина, называемая относительным

коэффициентом затухания колебательного звена .

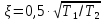К колебательным звеньям можно отнести R-L-C цепи, двигатель по­стоянного тока, электромашинный усилитель, механические элементы, обладающие массой, упругостью и вязким трением и др.

Операторные уравнения колебательного звена:

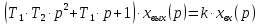; (3.21)

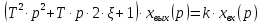. (3.22)

Передаточные функции колебательного звена:

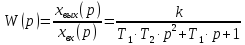; (3.23)

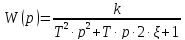. (3.24)

Характеристические уравнения колебательного звена:

,

. (3.25)

Отсюда корни характеристического уравнения

.

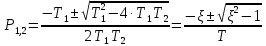Переходная функция колебательного эвена при ступенчатом входном воздействии x_вх= 1(t) будет описываться следующим уравнением:

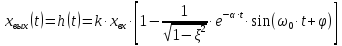, (3.27)

где 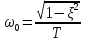-угловая частота собственных колебаний звена;

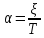- декремент затухания колебательного звена (чем больше

величина α, тем быстрее происходит уменьшение амплитуды коле­баний переходной функции);

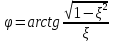- начальная фаза колебаний;

ξ-относительный коэффициент затухания.

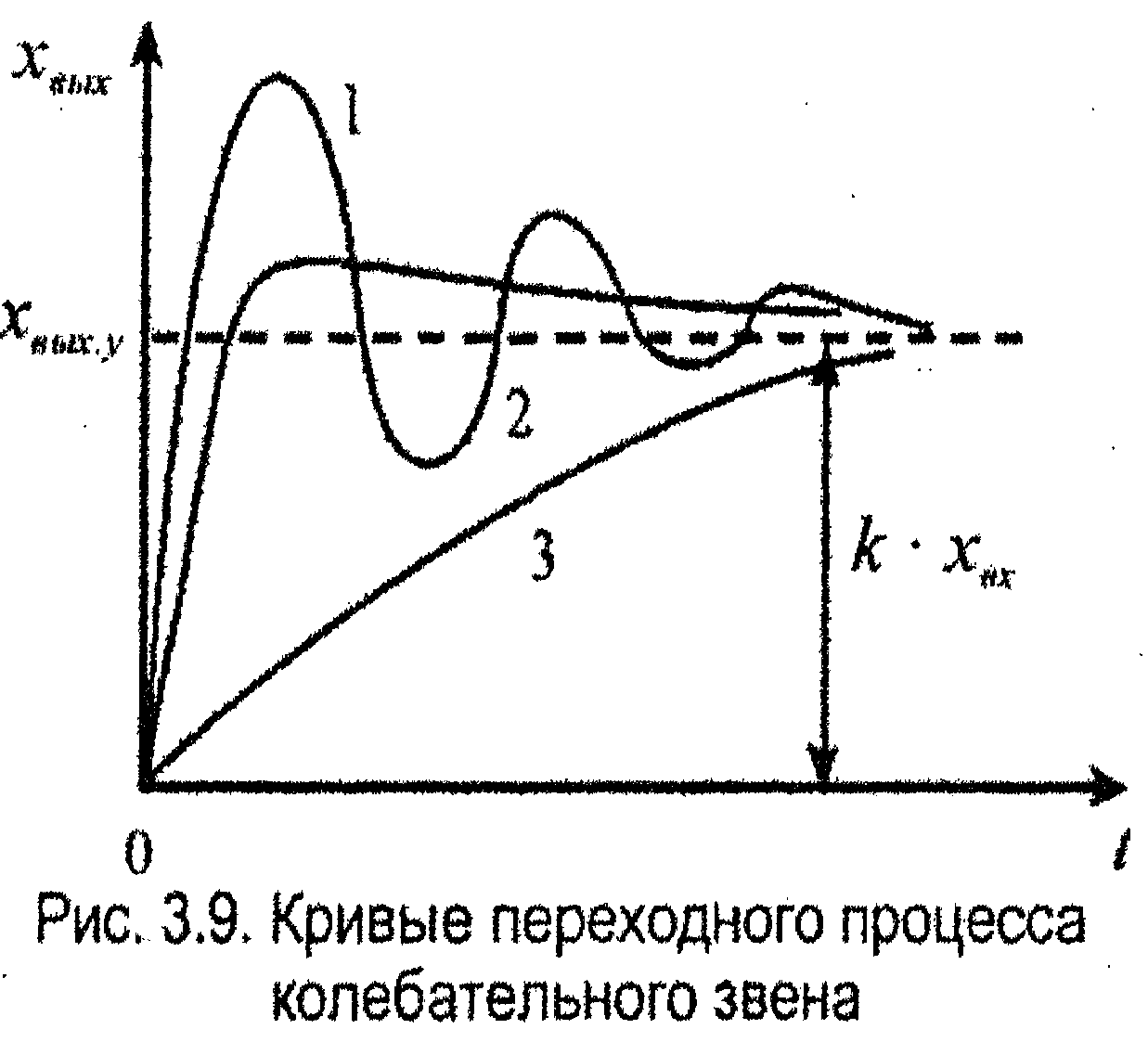
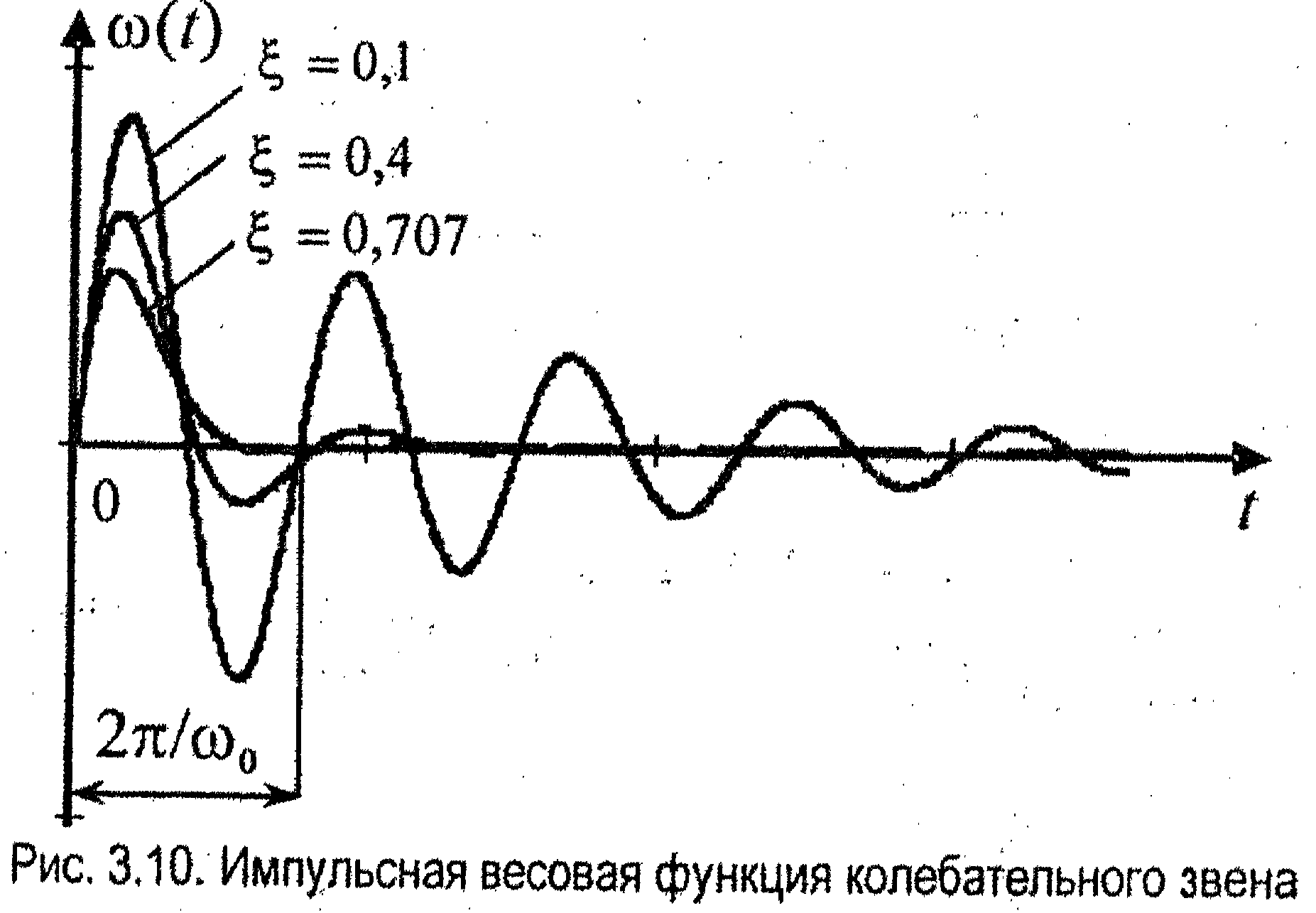
Это выражение характеризует затухающий колебательный процесс (рис. 3.9) с затуханием, определяемым величиной α и частотой ω.

Из выражения видно, что характер переходной функции зависит от коэффициента ξ.

1) При 0 < ξ < 1 - переходная функция имеет вид затухающих колебаний (при уменьшении ξ колебательность увеличивается).

2) При ξ=0 переходная функ­ция будет представлять собой неза­тухающие колебания, в данном слу­чае колебательное звено называет­ся консервативным и будет иметь передаточную функцию

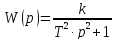
3) При -1 < ξ< 0 - на выходе звена со следующей переходной характеристикой

появляются возрастающие по амплитуде колебания.

Звено будет иметь следующую передаточную функцию:

,

т.е. является неустойчивым.

4) При ξ > 1 - переходная функция имеет монотонный характер и ко­лебательное звено превращается в апериодическое звено второго поряд­ка с передаточной функцией

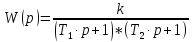, (3.28)

Если ξ»1, то Т₂«Т₁ и влиянием Т₂ на переходный процесс можно

пренебречь.

Импульсная переходная (весовая) функция (рис. 3.10)

.

АМПЛИТУДНО-ФАЗОВАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКА КОЛЕБАТЕЛЬНОГО ЗВЕНА

Уравнение АФХ колебательного звена может быть получено непосредственно из его передаточной функции подстановкой ϳω вместо р.

;

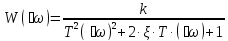(3.29)

или

,

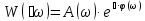где A(ω)- модуль АФХ W(ϳω).

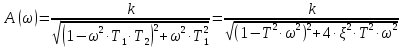, (3.30)

Где φ(ω)- аргумент амплитудно-фазовой характеристики звена.

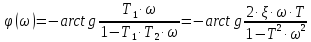. (3.31)

Частотные характеристики колебательного звена представлены на (рис. 3.11).

АФЧХ W(ϳω) колебательного звена может быть получена эксперимен­тально. В этом случае с её помощью можно определить параметры звена k, ξ и T. Величина коэффициента k равна длине отрезка на вещественной оси от начала координат до точки АФЧХ при ω=0.

Коэффициент ξ находится из выражения для отрезка

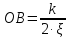
(см. рис. 3.11, б), т.е. .

Величина постоянной времени .

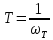ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ЗВЕНА

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) звена может быть получена следующим образом:

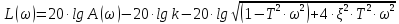. (3.32)

Первое слагаемое представляет собой постоянную величину L₁(ω)= 20∙lgК - прямую, параллельную оси абсцисс. Второе слагае­мое зависит от частоты ω.

Если , составляющими T²ω² и 4ξ²T²ω² можно пренебречь по сравнению с 1, поэтому L₂(ω)=0.

Если 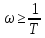,то выполняется условие 1« Т² ω².

В этом случае

.

Очевидно, что при изменении частоты ω на декаду, значение L₂(ω) изменится на -40 дБ. Следовательно, наклон L₂(ω) при этом будет равен -40 дБ/дек.

Таким образом, приближённая асимптотическая ЛАЧХ колебательного звена (рис. 3.12) изображается двумя отрезками прямых: горизонтальным отрез­ком, при 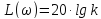, и отрезком с наклоном -40 дБ/дек. Низкочастотные и высокочастотные асимптоты ЛАЧХ сопрягаются при частоте сопряжения ω₁, определяемой из следующего уравнения , т.е. при

частоте .

Точные ЛАЧХ колебательного звена отличаются от асимптотической ЛАЧХ. Эти отклонения в значительной степени зависят от коэффициента относительного затухания ξ, входящего в выражение передаточной функции.

Добавляя поправки, соответствующие различ­ным значениям ξ, к асим­птотической ЛАЧХ, можно получить точные ЛАЧХ.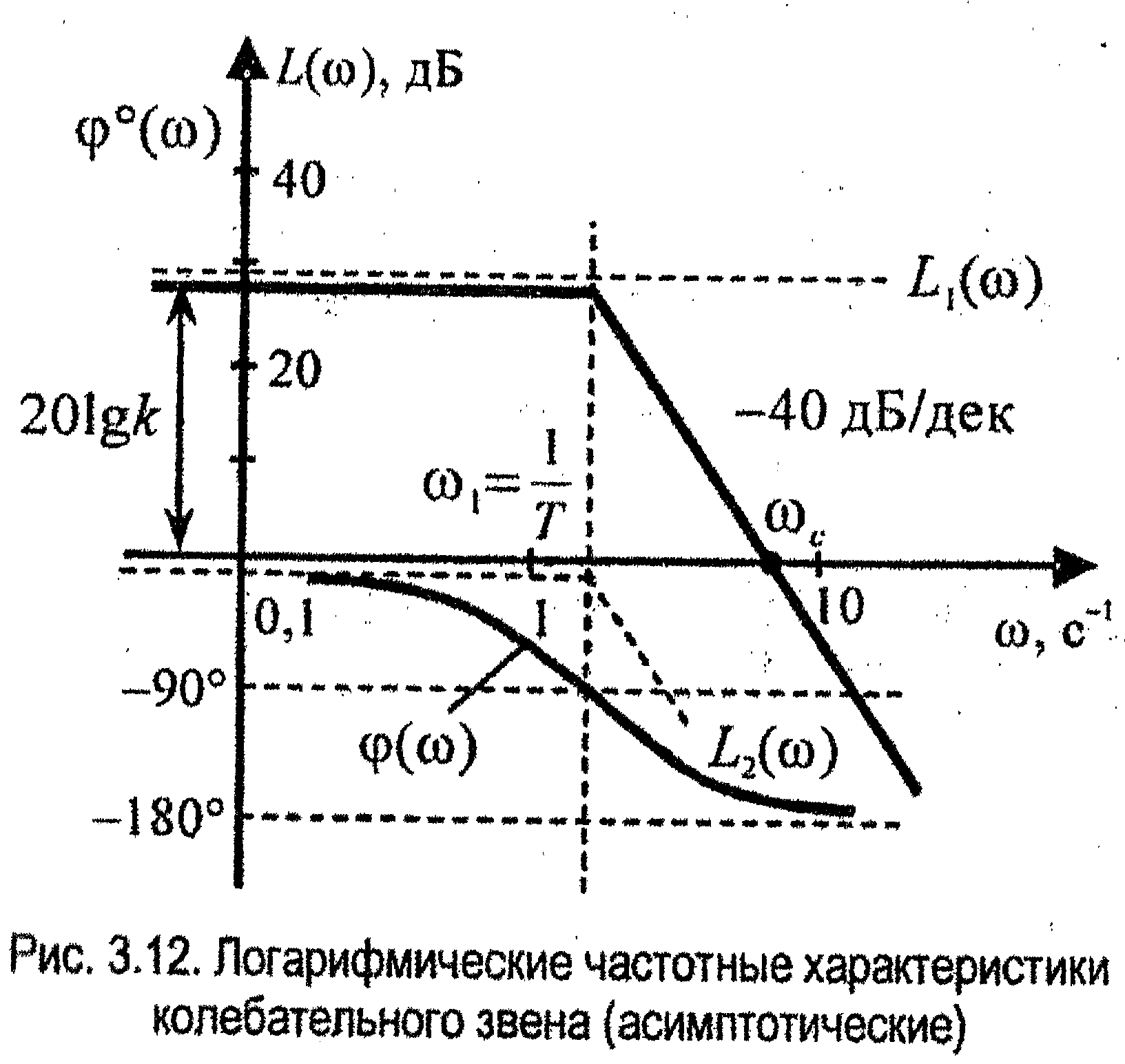

Если построить семей­ство кривых (ЛАЧХ) для одного и того же значения

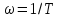и различных значений ξ, то можно пока­зать, что при значениях 0,35 < ξ< 0,75 расхождение между асимптотической и истинными ЛАЧХ не пре­вышает 3 дБ, как и в случае апериодического звена. Поэтому в этом случае можно пользоваться асимптотическими ЛАЧХ. При других значениях ξ асимптотическую ЛАЧХ корректируют с помощью готовых графиков поправок, даю­щих разность между истинной и асимптотической ЛАЧХ. L(ω) в этом случае строится по расчёт­ным точкам (рис. 3.13).

Если ξ = T₁/2Т₂ ≥1, то коле­бательное звено превращается в апериодическое звено второго по­рядка, описываемое передаточной функцией (3.28).

Корни характеристического уравнения в данном случае будут равны

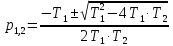. (3.33)

Импульсная переходная характеристика описывается уравнением (3.29). Если ξ=0, то колебательное звено превращается в консервативное звено.

Логарифмическая фазочастотная характеристика колебательного зве­на φ(ω) рассчитывается по формулам:

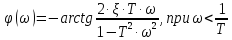; (3.34)

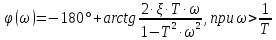. (3.35)

На рис. 3.13 представлены эти характеристики при различных значени­ях коэффициента ξ, из которых видно, что ЛФЧХ колебательного звена изменяется от 0° в области низких частот, до 180^° в области высоких час­тот. На частоте сопряжения сдвиг по фазе равен -90°.