мат. модел в почв

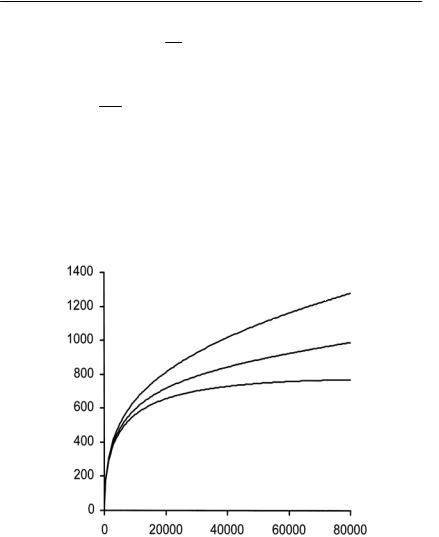
Часть I. Построение математических моделей

de

скорости выветривания и перемещения почвы в результате

dt

эрозии, которая определяется эрозионной диффузией (D) и кри

визной склона d2 z . dx2

Уравнение (5.15) может быть решено численно с учетом соот ветствующих начальных и граничных условий.

В качестве иллюстрации на рис. I.5.5 представлены кривые динамики мощности почвенной толщи в гипотетическом ланд шафте, рассчитанные по уравнению (5.15).

Рис. I.5.5. Изменение мощности почвы во времени в гипотетическом ландшафте в долине, средней части склона и на холме. (по Minasny, McBratney, 1999)

181

Математическое моделирование в почвоведении

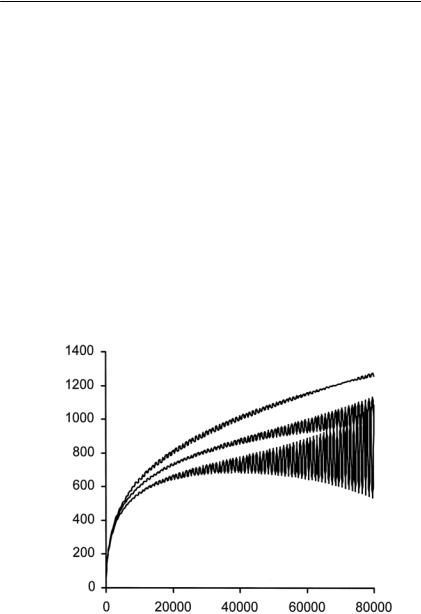
Исследование модели свидетельствует о высокой чувстви тельности к начальным условиям, свойственной нелинейной сис темам. Как обсуждалось в третьей главе, нелинейные системы характеризуется сложной и многообразной динамикой. В их по ведении возможно обнаружение детерминированного хаоса – режима с очень изменчивой амплитудой. Хаотическое поведение обусловлено тем, что небольшие отклонения от начальных усло вий в нелинейных системах со временем могут увеличиваться, в результате чего первоначально близкие траектории будут расхо диться. Рис. I.5.6 демонстрирует периодические флуктуации мощ ности почвенной толщи при малых изменениях начальных усло вий. Флуктуации могут быть меньшими или большими в зависи мости от положения почвы на склоне.

Рис. I.5.6. Изменение мощности почвы со временем в долине, середине склона и на холме. При выполнении расчетов с временным шагом 500

182

Часть I. Построение математических моделей

лет и вводом малых различий начальных условий (по Minasny, McBrat ney,1999).

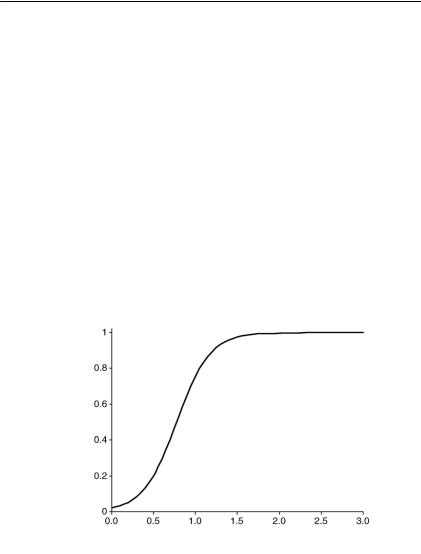
В дальнейшем обсуждаемая модель была усовершенствова на за счет перехода от одномерного (1D) к двумерному (2D) вари анту и включения описания химического выветривания, приво дящего к уменьшению мощности почвенной толщи в результате растворения минералов и выщелачивания растворенного вещест ва (Minasny, McBratney, 2001). Важным шагом в развитии модели явилось описание обратной связи, характеризующей снижение эрозии почвы при увеличении продуктивности растительного по крова. С этой целью в модель введен индекс продуктивности – функция, изменяющаяся от 0 до 1 в зависимости от мощности почвы (рис. I.5.7) (Minasny, McBratney, 2006).

Продуктивность

Мощность почвы (м)

Рис. I.5.7. Индекс продуктивности в зависимости от мощности почвен ной толщи (по Minasny, McBratney,2006).

В моделях развития ландшафта почва представлена одним слоем, мощность которого изменяется на протяжении десятков и сотен тысяч лет. Сальвадор Бланес с соавт. (Salvador Blanes et al., 2007) попытались построить модель почвообразования в масшта бе почвенного профиля, подходящую для включения в модель

183

Математическое моделирование в почвоведении

развития ландшафта (Minasny, McBratney, 2001). Она включает физическое выветривание грубой и тонкой фракций почвы, хими ческое выветривание тонкой фракции, процессы деформации и биотурбации и описывает, как со временем в результате развития почвы изменяется внутрипрофильное распределение ее плотно сти, содержания грубой и тонкой фракций и минералогического состава. Обсуждаемая модель имитирует образование почвенных горизонтов в результате только физико химического выветрива ния, процессов деформации и биотурбации и не описывает про цессы переноса вещества, обусловленные циркуляцией воды в почве и играющие важную роль в дифференциации профиля. Тем не менее, она играет важную роль в развитии ландшафтных мо делей, так как это первый шаг в направлении перехода к моде лям, описывающим изменение во времени не только мощности почвенного профиля, но и образование горизонтов.

Для того чтобы познакомиться с моделями педогенеза второй группы, которые описывают как в результате почвообразования формируются почвенные горизонты в исходно однородной поч вообразующей породе, рассмотрим модель элювиального про цесса УИП5, предложенную А.И. Морозовым (Морозов, 1988) и

модель SoilGen (Finke, Hutson, 2008; Finke, 2012; Opolot et al. 2015).

Разработка моделей формирования почвенного профиля из исходной почвообразующей породы является оной из централь ных задач теоретического почвоведения. Одним из первых ре шить эту задачу попытался А.И. Морозов. Начиная, с 1988 года он опубликовал цикл работ, представляющих серию последователь но усложняющихся динамических моделей педогенеза, пред ставляющих, как формируются почвенные горизонты в исходно однородной почвообразующей породе в процессе почвообразо вания. Серия включает модель элювиального процесса УИП 5 (УИП – это Уравнения «Идеального» Подзола, цифра указывает на число уравнений в модели), модель элювиально иллювиального процессов (УИП 6) и модель, включающая процессы оглеения (УИП 9) (Морозов, 1988; Морозов и др., 1990; 1993; Морозов, Тар гульян, 1995).

184

Часть I. Построение математических моделей

К вопросу о… Александр Иванович Морозов (1928 2008) в 2007 году опуб ликовал книгу «О почве и почвоведении (взгляд со стороны)», которая вызвала большой интерес и активную дискуссию в сре де почвоведов (А.И. Морозов. О почве и почвоведении (взгляд со стороны). М.: ГЕОС, 2007, 286 с.). В предисловии к этой книге Л.О. Карпачевский отмечает ее оригинальность и богатство идеями и новыми подходами к решению самых разных вопросов почвоведения. А.И. Морозова, который был по специальности физиком теоретиком и известным специалистом в области плазмодинамики, отличало разнообразие научных интересов и широкий кругозор. Он говорил, что почвы привлекли его внима ние «поражающей эффективностью и таинственностью функционирования». В воспоминаниях о профессоре кафедры почвоведения МГУ им М.В. Ломоносова Е.М. Самойловой, с кото рой он много и успешно сотрудничал, А.И. Морозов писал: «В си лу моего профессионального склада, мне захотелось построить математическую модель почвы. При этом меня интересовало не описание какого либо конкретного процесса, например, пере носа влаги или солей – этим занимались многие, в частности, в связи с проблемой мелиорации почв – мне хотелось построить модель почвы в целом или, хотя бы, модель почвы определенно го типа». Основное внимание он уделял вопросам математиче ской формализации почвоведения, считая, что центральной за дачей теоретического почвоведения является построение мо дели почвы как целого «т.е. как совокупности генетических го ризонтов, как некой развивающейся системы, порождающей эти горизонты». А.И. Морозов предложил методологию мате матической формализации почвоведения. Он писал, что наибо лее фундаментальные свойства почв, могут быть описаны простыми внутренне замкнутыми системами уравнений и предлагал начать с построения минимальных базовых моделей, которые в дальнейшем должны обогащаться путем включения новых уравнений, все более детально учитывающих особенно сти конкретных процессов в конкретных условиях. А.И. Морозов

185

Математическое моделирование в почвоведении

надеялся, что «Благодаря этому на неком уровне своего разви тия такое («теоретическое») почвоведение должно стать мощным практическим инструментом прогнозирования дина мики реальных почв». Он одним из первых начал работать в этом направлении. Им разработаны базовые модели формиро вания почвы в результате элювиального, элювиально иллювиального процессов и оглеения. В соавторстве с Т.А. Соколовой предложена модель динамики гранулометриче ского состава мономинеральной почвы (Морозов, Соколова, 1991). На основе концепции А.Д. Фокина построена оригинальная модель динамики гуматного гумуса в соавторстве с Е.М. Самойловой (Морозов А.И., Самойлова Е.М., 1993). Работы А.И. Морозова имеют основополагающее значение для разви тия математической педодинамики. К сожалению, ссылки на эти работы пока не вошли в современные обзоры моделей пе догенеза.

В качестве примера рассмотрим первую модель из этой се рии УИП5. Автор назвал ее моделью «идеального подзола», что бы подчеркнуть, что речь идет не о моделировании формирова ния конкретного реального профиля, а об абстрактном профиле. Суть этой идеализации заключается в предположениях, лежащих в основе модели.

Предположения, принятые при построении модели УИП5

Для простоты в модели не рассматривается латеральный пе ренос вещества, поэтому поверхность принята статичной.

Предполагается, что в начальный момент времени есть гомо генная рыхлая водопроницаемая почвообразующая порода. Это может быть гомогенная толща песка, обеспечивающая свободную фильтрацию воды с растворенными в ней веществами сквозь всю элювиируемую толщу. Песок состоит из двух минералов: конгру ентно растворимого силиката (например, средне основного пла гиоклаза) и практически нерастворимого (или очень медленно растворимого) минерала, например, кварца. На поверхность по

186

Часть I. Построение математических моделей

роды непрерывно поступает поток влаги, содержащей растворен ное органическое вещество любой природы. Поступающий рас твор является агрессивным по отношению к породе и условно на зван «фульво». Такой поток вертикально просачивается с посто янной скоростью через всю толщу. Проникая вглубь, поток влаги с растворенным «агрессором» взаимодействует с породой так, что полностью и конгруэнтно растворяет «плагиоклазы». Все продук ты разрушения выносятся в растворенной форме за пределы элю виальной толщи, а нерастворимая часть породы «кварц» остаточ но накапливается в зоне элювиирования.

Эта схема «идеального» элювиального процесса, конечно, сильно упрощает реальный элювиальный процесс, но, тем не ме нее, она отражает его существенные черты в некоторых почвах гумидных областей: промывной водный режим; наличие в посту пающих и просачивающихся растворах веществ – агрессоров, спо собных разрушать почвообразующие породы; наличие условий свободного выноса из зоны элювиирования продуктов растворе ния минералов. Она вполне приложима к формированию подзо листого горизонта в песчаных подзолах.

Модель «идеального подзола» УИП 5, описывает динамику следующих пяти переменных состояния: влаги (w), «фульво» (f); материнской породы (m1); «кварца» (m2); «биофила» (с). «био фил» – это вещество, образующиеся в результате растворения ма теринской породы под действием «фульво». Предполагается, что материнская порода взаимодействует с «фульво» по схеме: m1 + f = m2 + c. Размерность переменных состояния (г/см3). В од номерном варианте, когда все величины зависят только от одной пространственной координаты z, направленной вертикально вниз, она представляет собой систему пяти дифференциальных уравнений следующего вида:

187

Математическое моделирование в почвоведении

5)dm2 =μ2βfm1 = −μ2 dm1 , dt dt

где vw – скорость перемещения влаги в почве; Dw, Df, Dc – ко эффициенты диффузии влаги, «фульво» и «биофила» (два по следних по отношению к влаге) в почве, τf – скорость «самораспа да» «фульво» – исчезновение, не связанное с переносом или ре акцией с материнской породой; β – константа скорости разложе ния материнской породы; µf , µc , µ2 – параметры (отношения мо лекулярных масс «фульво», «биофила» и кварца и соответствую щих молекулярных масс породы); А(z,t) – безразмерный корневой фактор, характеризующий распределение активности корней, аw, аc – параметры поглощения корнями влаги и «биофила» соответ ственно.

В (5.16) уравнение (1) описывает динамику влаги в почве. Первое слагаемое в правой части этого уравнения описывает диффузию влаги в почве (Dw – коэффициент диффузии), а второе ее поглощение корнями. А(z,t) характеризует распределение ак тивности корней. Динамику «фульво» описывает уравнение (2), в левой части которого представлен конвективный перенос «фуль во» водой. В правой части этого уравнения учтена диффузия «фульво» в растворе (Df), самораспад «фульво» за характерное время τf, под которым понимаются любые процессы, приводящие к разложению или потере активности, и «гибель» «фульво» в ре зультате связывания с материнской породой. Уравнение (3) ха рактеризует скорость разложения материнской породы с посто янным кинетическим коэффициентом β. Уравнения (4) и (5) опи сывают динамику «биофила» и кварца соответственно.

Для решения системы (5.16) нужно задать начальные и гра ничные условия. Начальные условия – это распределение по z для переменных состояния модели. Для простоты принято, что в на чальный момент кварц, «фульво» и «биофил» в почве отсутству

188

Часть I. Построение математических моделей

ют. Граничные условия. Поскольку рассматриваются три мигри рующих по профилю почв субстанции, описывемые уравнениями в частных производных (уравнения 1, 2, 4) для них должны быть заданы условия на поверхности z = 0 и на нижней границе поч венного профиля z = L. На поверхности были заданы постоянные потоки влаги, «фульво» и «биофила». На нижней границе следует ставить условия на интенсивность просачивания влаги и раство ренных веществ. В простейшем случае, можно считать, что проса чивания за нижнюю границу не происходит.

Рассматриваемая модель использовалась для анализа дина мики фронта элювиирования (ФЭ). Фронт элювиирования – зона перехода от области неразрушенной породы к области, где эта порода полностью разрушена. Правильнее говорить о зоне пере хода, ниже которой разрушено, например <30% материнской по роды, а выше сохранилось неразрушенной около 30% материн ской породы. Модель позволяет ответить на следующие вопросы:

1.Представляет ли фронт элювиирования после некоторой ста дии формирования «стационарную» в дальнейшем структу ру, или его параметры (например, толщина) непрерывно из меняются?

2.Если ФЭ выходит в стационарное состояние, то каково время выхода в это состояние?

3.Чем определяется толщина фронта элювиирования?

4.От чего зависит скорость перемещения ФЭ вглубь толщи

материнской породы?

Результаты выполненных численных расчетов с реалистиче скими значениями кинетических коэффициентов находятся в ра зумном согласии с данными наблюдений. Представленные мате риалы свидетельствуют об эффективности модели УИП 5. Эта мо дель относится к типу базовых «минимальных» моделей. Их ис пользуют для изучения основных динамических свойств системы, поэтому они имеют предельно простую «минимальную» структу ру, при их построении стараются по возможности исключить де тали, чтобы понять суть изучаемых явлений. Полученные резуль таты свидетельствуют о целесообразности развития моделей пе догенеза этого типа.

189

Математическое моделирование в почвоведении

Следующая модель педогенеза SoilGen, которую мы рассмот рим, относится к классу более детальных имитационных моделей

(Finke, Hutson, 2008; Finke, 2012; Opolot et al., 2015). Она предна значена для изучения педогенеза в масштабе нескольких тысяче летий (до 15000 лет). SoilGen описывает формирование почвенно го профиля в результате взаимодействия биологических, геохи мических и физических процессов. Очень существенно, что SoilGen отражает связь факторов почвообразования («CLORPT») с процессами почвообразования (табл. 5.1). Модель описывает вертикальный перенос тепла, влаги, растворенных веществ, ми грацию глины, физическое и химическое выветривание, различ ные химические равновесия, катионный обмен, корневое погло щение элементов, круговорот углерода, диффузионный поток СО2 и биотурбации. Кроме того, она отражает антропогенное воздей ствие на почвообразование, учитывая эрозию, вспашку и внесе ние удобрений. В SoilGen процессы вертикального переноса в почве воды и растворенных веществ моделируются аналогично модели LEACHCM, описывающей движение воды и растворенных веществ в ненасыщенной зоне (Hutson, 2003).

Взаимодействие между почвой и растительностью в SoilGen представлено ежегодным поступлением опада и корневым по глощением ионов. Параметры, характеризующие эти процессы, определяются одним из четырех типов растительного покрова (травы/кустарники, сельскохозяйственные культуры, хвойные и широколиственные леса). Углеродный цикл описан в соответствии с Ротамстедской моделью RothC 26.3 (Jenkinson, Coleman, 1994).

Процессы почвообразования, имитируемые SoilGen, имеют раз ный временной масштаб от миллисекунд до тысяч лет. Поэтому вычисления для разных процессов проводятся с разным шагом по времени. Например, теплоперенос моделируется с часовым ша гом, превращения органического вещества вычисляются с суточ ным шагом, а биотурбации с ежегодным. Однако все выходные данные представляются с годовым шагом (Opolot et al., 2015).

190