
- •Введение
- •Блага, множество допустимых альтернатив
- •Бинарные отношения и их свойства
- •Задачи
- •Неоклассические предпочтения
- •Задачи
- •Представление предпочтений функцией полезности
- •Задачи
- •Свойства предпочтений и функции полезности
- •Задачи
- •Рационализация наблюдаемого выбора
- •Задачи
- •Непротиворечивые, но неполные предпочтения
- •Полные, но противоречивые (нетранзитивные) предпочтения
- •Задачи
- •Поведение потребителя
- •Модель поведения потребителя: основные понятия и свойства
- •Бюджетное множество
- •Задача потребителя, маршаллианский спрос, непрямая функция полезности
- •Задача минимизации расходов и хиксианский спрос
- •Задачи
- •Дифференциальные свойства задачи потребителя
- •Задачи
- •Влияние изменения цен и дохода на поведение потребителя
- •Сравнительная статика: зависимость спроса от дохода и цен. Закон спроса
- •Оценка изменения благосостояния.
- •Задачи
- •Рационализация. Теорема Африата
- •Задачи
- •Восстановление квазилинейных предпочтений
- •Восстановление предпочтений на основе функции расходов
- •Проблема восстановимости предпочтений на всем множестве потребительских наборов
- •Интегрируемость (рационализуемость) спроса
- •Задачи
- •Задачи к главе
- •Поведение производителя
- •Технологическое множество и его свойства
- •Задачи
- •Задачи
- •Задачи
- •Затраты и издержки
- •Множество требуемых затрат
- •Функция издержек
- •Восстановление множества требуемых затрат
- •Задачи
- •Агрегирование в производстве
- •Задачи
- •Классическая модель экономики. Допустимые состояния
- •Общее равновесие (равновесие по Вальрасу)
- •Субъекты экономики в моделях общего равновесия
- •Модели общего равновесия
- •Некоторые свойства общего равновесия
- •Избыточный спрос
- •Задачи
- •Существование общего равновесия
- •Задачи
- •Парето-оптимальные состояния экономики и их характеристики
- •Характеризация границы Парето через задачу максимизации взвешенной суммы полезностей
- •Дифференциальная характеристика границы Парето
- •Задачи
- •Связь равновесия и Парето-оптимума. Теоремы благосостояния
- •Задачи
- •Существование равновесия в экономике обмена
- •Характеристика Парето-оптимальных состояний
- •Характеристика поведения потребителей
- •Потребительский излишек: определение, связь с прямой и обратной функциями спроса
- •Характеристика поведения производителей
- •Излишек производителя
- •Связь излишков с благосостоянием
- •Репрезентативный потребитель
- •Задачи к главе
- •Риск и неопределенность
- •Представление предпочтений линейной функцией полезности
- •Представление линейной функцией полезности: доказательство
- •Задачи
- •Предпочтения потребителя в условиях неопределенности
- •Задачи
- •Задача потребителя при риске
- •Задачи
- •Модель инвестора (выбор оптимального портфеля)
- •Задачи
- •Сравнительная статика решений в условиях неопределенности
- •Задачи
- •Задачи
- •Задачи к главе
- •Задачи
- •Равновесие Раднера в экономике с риском
- •Задачи
- •Задачи к главе
- •Налоги
- •Общее равновесие с налогами, не зависящими от деятельности
- •Общее равновесие с налогами на потребление
- •Задачи
- •Общее равновесие с налогами на покупку (продажу)
- •Задачи
- •Оптимум второго ранга. Налог Рамсея
- •Задачи
- •Задачи
- •Экстерналии
- •Модель экономики с экстерналиями
- •Проблема экстерналий
- •Задачи
- •Свойства экономики с экстерналиями
- •Задачи
- •Равновесие с квотами на экстерналии
- •Равновесие с налогами на экстерналии
- •Задачи
- •Рынки экстерналий
- •Задачи
- •Альтернативная модель экономики с экстерналиями
- •Задачи
- •Экстерналии в квазилинейной экономике
- •Задачи
- •Слияние и торг
- •Задачи
- •Торговля квотами на однородные экстерналии
- •Задачи
- •Задачи к главе
- •Общественные блага
- •Задачи
- •Квазилинейная экономика с общественными благами
- •Задачи
- •Равновесие с добровольным финансированием
- •Задачи
- •Равновесие (псевдоравновесие) Линдаля
- •Задачи
- •Долевое финансирование: общие соображения
- •Задачи
- •Голосование простым большинством
- •Равновесие с политическим механизмом
- •Задачи
- •Задачи
- •Задачи к главе
- •Примеры торга при асимметричной информации
- •Покров неведения и конституционный контракт
- •Задачи
- •Модели рынка с асимметричной информацией
- •Модификация классических моделей равновесия: равновесия с неотличимыми благами
- •Модель Акерлова: классическая постановка
- •Модель Акерлова как динамическая игра
- •Задачи
- •Монополия
- •Классическая модель монополии
- •Сравнительная статика
- •Анализ благосостояния в условиях монополии
- •Существование равновесия при монополии
- •Задачи
- •Ценовая дискриминация
- •Дискриминация первого типа. Идеальная дискриминация
- •Дискриминация второго типа (нелинейное ценообразование)
- •Задачи
- •Олигополия
- •Модель Курно
- •Свойства равновесия Курно в случае постоянных и одинаковых предельных издержек
- •Свойства равновесия Курно в случае функций издержек общего вида
- •Равновесие Курно и благосостояние
- •Модель Курно и количество фирм в отрасли
- •Задачи
- •Модель дуополии Штакельберга
- •Существование равновесия Штакельберга
- •Равновесие Штакельберга и равновесие Курно
- •Приложение
- •Задачи
- •Картель и сговор
- •Неоптимальность равновесия Курно с точки зрения олигополистов
- •Сговор
- •Картель
- •Задачи
- •Модель Бертрана
- •Продуктовая дифференциация и ценовая конкуренция
- •Модель Бертрана при возрастающих предельных издержках
- •Динамический вариант модели Бертрана (повторяющиеся взаимодействия)
- •Задачи
- •Модель олигополии с ценовым лидерством
- •Задачи
- •Модели найма
- •Модель с полной информацией
- •Задачи
- •Модель с ненаблюдаемыми действиями
- •Формулировка модели и общие свойства
- •Дискретный вариант модели со скрытыми действиями
- •Задачи
- •Модель найма со скрытой информацией
- •Модель найма со скрытой информацией при монопольном положении нанимателя: характеристики оптимальных пакетных контрактов
- •Модель найма с асимметричной информацией при монопольном положении нанимателя: общий случай
- •Задачи
- •Конкуренция среди нанимателей в условиях скрытой информации
- •Задачи
- •Модель сигнализирования на рынке труда (модель Спенса)
- •Введение
- •Статические игры с полной информацией
- •Нормальная форма игры
- •Концепция доминирования
- •Равновесие по Нэшу
- •Равновесие Нэша в смешанных стратегиях
- •Динамические игры с совершенной информацией
- •Динамические игры с несовершенной информацией
- •Статические игры с неполной информацией
- •Динамические байесовские игры
- •Игры и Парето-оптимальность
- •Сотрудничество в повторяющихся играх
- •Игры торга
- •Вогнутые и квазивогнутые функции
- •Однородные функции
- •Теорема Юнга
- •Теоремы о неподвижной точке
- •Теоремы отделимости
- •Теорема об огибающей
- •Свойства решений параметрической задачи оптимизации
- •Теоремы о дифференцируемости значения экстремальной задачи

11.6. Голосование простым большинством |
417 |
Ясно, что равновесие при консенсусе может существовать лишь при специальном подборе долей финансирования. Поэтому рассмотренная здесь концепция равновесия имеет, как и равновесие Линдаля, только теоретическое значение. Его можно использовать как своего рода исходный пункт при анализе долевого финансирования. В общем случае, при произвольно выбранных долях финансирования общественного блага, нет оснований ожидать, что при любых рыночных ценах желаемые объемы потребления общественных благ у всех потребителей будут совпадать. Поэтому возникает проблема согласования их предпочтений относительно этих количеств.
Другими словами, в концепции равновесия с долевым финансированием способ финансирования общественных благ следует дополнить некоторым механизмом принятия коллективных решений об объемах производства общественных благ, который бы «работал» и при отсутствии консенсуса. Ниже приводятся примеры таких механизмов.
11.5.1Задачи
/ 512. В квазилинейной экономике с общественным благом имеются два потребителя с функциями полезности вида:
u1 = av(x) + z1 и u2 = bv(x) + z2 (a, b > 0).
Производная v0(x) положительна и убывает. Единственный производитель имеет функцию издержек вида c(y) = 4y.
Финансирование общественного блага осуществляется на долевой основе с долями δ1 и δ2 . Известно, что был достигнут консенсус. Что можно сказать об отношении долей δ1/δ2 ? Обоснуйте свое утверждение.
/ 513. В квазилинейной экономике с общественным благом имеются два потребителя с функциями полезности вида:
u1 = av(x) + z1 и u2 = bv(x) + z2 (a, b > 0).
Производная v0(x) положительна и убывает. Единственный производитель имеет функцию издержек вида c(y) = 5y.
Финансирование общественного блага осуществляется на долевой основе с долями 2/3 и 2/3. При каких условиях на a и b в этой экономике не может быть достигнут консенсус? Обоснуйте свое утверждение.
11.6Долевое финансирование с равновесием при голосовании простым большинством
Один из самых распространенных механизмов принятия общественных решений (процедур коллективного выбора) — это голосование.
При анализе голосования мы будем исходить из предпочтений потребителей на наборах общественных благ (при заданных рыночных ценах и структуре общественных расходов). Для этого рассмотрим следующие задачи:
ui(x(1), x(2)i ) → max
XX
δik(xk)pkxk + |
pkxik6βi, |
(11.5) |
k K1 |
k K2 |
|
(x(1), x(2)i ) = xi Xi,

11.6. Голосование простым большинством |
418 |
где полезность максимизируется по x(2)i при заданной величине x(1) . На основе этих задач предпочтения можно задать с помощью функции полезности u˜i(·), сопоставляющей каждому набору общественных благ x(1) максимально достижимое значение полезности в данной задаче.
Одна из самых распространенных процедур — голосовании по правилу простого большинства.
Определение 78:
Пусть A — множество альтернатив и {<i}i — набор предпочтений i = 1, . . . , m на A. Альтернатива a¯ A называется равновесием при голосовании по правилу простого большинства
если не существует такой альтернативы a A, что она лучше a¯ по большинству предпочтений.
На основе этой процедуры можно предложить концепцию равновесия для экономики с общественными благами.
Определение 79:
Равновесие с долевым финансированием и голосованием на основе правила простого большинства есть набор (p¯, x¯, y¯), такой что18
???list # (x¯, y¯) — допустимое состояние экономики с общественными благами;
# для каждого потребителя x¯(2)i является решением задачи (11.5) при ценах p, доходах
X
βi = p¯ωi + γijp¯y¯j + Si
j J
иобъемах потребления общественных благ x(1) = x¯(1) ;
#x¯(1) — равновесие при голосовании по правилу простого большинства для альтернатив, заданных множеством наборов общественных благ X(1) , и набора предпочтений, заданных
функциями u˜i(·);
# каждая технология y¯j является решением соответствующей задачи производителя (11.3) при ценах p¯ .
Выбор количества общественных благ с помощью голосования простым большинством сталкивается с двумя серьезными проблемами:
(1)Такое равновесие существует только при довольно ограничительных предположениях. Известный парадокс Кондорсе19 показывает, что, вообще говоря, при числе участников не менее трех (> 3) равновесие при голосовании может не существовать даже при конечном числе альтернатив.
(2)Даже если равновесие существует, оно обычно не Парето-оптимально.
Существование равновесия при голосовании можно гарантировать в случае, когда предпочтения потребителей однопиковые.
Приведем определение понятия однопиковых предпочтений для частного случая, когда множество альтернатив A является подмножеством действительных чисел (этот случай соответствует экономике, в которой существует только одно общественное благо). Отношение
18По-видимому, впервые голосование по поводу выбора объема общественного блага было проанализировано Говардом Боуэном в статье H. R. Bowen: The Interpretation of Voting in the Allocation of Economic Resources,
Quarterly Journal of Economics 58 (1943): 27–48.
19 Жан Антуан Кондорсе (Marie Jean Antoine Nicolas de Caritat marquis de Condorcet), 1743-1794 — французский математик и социолог.
В примере Кондорсе рассматриваются 3 участника, выбирающие из 3 альтернатив. Парадокс возникает, когда предпочтения заданы следующим образом:
a1 1 a2 1 a3, a3 2 a1 2 a2, a2 3 a3 3 a1.
11.6. Голосование простым большинством |
419 |
предпочтения <i потребителя (на множестве альтернатив A) однопиковое, если выполняются следующие условия:
(a) существует оптимальная с точки зрения потребителя i альтернатива aˆi (альтернатива aˆi такая, что aˆi <i a для всех a A);
(b)если a1 6 a2 6 aˆi , то a2 <i a1 ;
(c)если a1 > a2 > aˆi , то a2 <i a1 .
Проиллюстрируем сказанное на примере квазилинейной экономики. Пусть доля δi каждого потребителя в финансировании общественного блага постоянна и положительна. Тогда предпочтения потребителя i на множестве возможных вариантов потребления общественного блага задаются функцией
u˜i(x) = vi(x) − δipx.
Будем считать, что для любого i функция u˜i(x) достигает максимума на множестве неотрицательных чисел при любом положительном p. Обозначим это оптимальное с точки зрения потребителя i количество общественного блага xˆi 20. Тогда соответствующие предпочтения являются однопиковыми (при aˆi = xˆi ) на множестве альтернатив A = [0, ∞).
Действительно, по построению величина xˆi — максимум функции u˜i(x) на множестве A. Несложно также проверить, что, поскольку vi0(x), не убывает, эти предпочтения удовлетворяют условиям (b) и (c).
Заметим, что величину u˜i(ˆxi) = vi(ˆxi) − δipxˆi можно интерпретировать как потребительский излишек, соответствующий индивидуализированной цене общественного блага δip.
Если предельные издержки vi0(·) являются непрерывной функцией, то xˆi удовлетворяет
соотношениям
vi0(ˆxi) 6 δip,
причем, если xˆi > 0, то
vi0(ˆxi) = δip.
Эти уравнения задают равновесие.
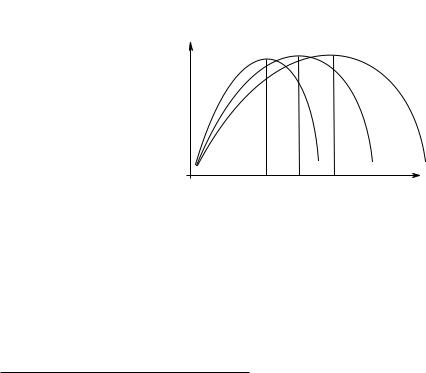
Возможное поведение оценок u˜i(xi) объемов общественного блага для случая, когда m = 3, приведено на диаграмме:
u˜1 |
(x) |
u˜3 |
(x) |
|
|
u˜2(x)
xˆ1 xˆ2 xˆ3 |
x |
Заметим, что в случае, когда m — нечетное число (m = 2s + 1), равновесие при голосовании имеет особо простую структуру. В этом случае равновесной является медиана из объемов xˆi , то есть (s + 1)-й по порядку возрастания объем. (Если все величины xˆi разные, ровно s = (m − 1)/2 потребителей предпочитает увеличить потребление общественного блага, а другие s потребителей желали бы его уменьшить). В приведенном на диаграмме примере это альтернатива xˆ2 . Таким образом, равновесие при голосовании определяется предпочтениями медианного потребителя. Обозначим индекс такого потребителя через i . Заметим, что i , вообще говоря, зависит от цены общественного блага p, поскольку от p зависят функции u˜i(x).
20Условие vi0(xi) → 0 при xi → ∞ гарантирует существование такого количества.

11.6. Голосование простым большинством |
420 |
Учитывая сказанное, (внутреннее) равновесие на рынке общественного блага в состоянии равновесия с долевым финансированием и голосованием на основе правила простого большинства характеризуется следующим образом. Если y¯ — равновесный объем, а p — равновесная цена общественного блага, то
p = c0(¯y) и xˆi = y,¯
где i — медианный потребитель при цене p.
Вобщем случае при нахождении равновесия для нахождения медианного потребителя нужно знать равновесную цену, которая, в свою очередь, зависит от медианного потребителя (желаемого им объема потребления общественного блага).
Но если предельные издержки производства общественного блага постоянны, то (во внутреннем равновесии) равновесная цена известна заранее — она равна предельным издержкам
иi — медианный потребитель при этой цене.
Вобщем случае найти медианного потребителя при «правильной» цене можно на основе
следующего приема.
Заметим сначала, что поскольку p = c0(ˆxi ), то величина xˆi является решением одного из следующих m уравнений
vi0(xi) = δic0(xi).
Предположим, что x¯i — медиана из рассматриваемых величин {x¯i} — решений таких уравнений. Тогда x¯i является предпочитаемым медианным потребителем объемом потребления общественного блага (то есть xˆi = x¯i ), а величина p¯ = c0(¯xi ) — равновесной ценой общественного блага.
Для доказательства этого факта достаточно показать, что при цене p¯ = c0(¯xi ) потребитель i является медианным потребителем. Покажем это. Для каждого потребителя i, такого что x¯i 6 x¯i , величина c0(¯xi) не превышает величину равновесной цены p¯ = c0(¯xi ). Поэтому предпочитаемое при цене p потребителем i количество общественного блага xˆi — решение уравнения vi0(xi) = δip¯ — не превышает величину x¯i . Таким образом xˆi 6 xˆi . Аналогичным образом показывается, что если x¯i > x¯i , то xˆi > xˆi . А это и означает, что потребитель i является медианным при ценах p¯ = c0(¯xi )21.
С другой стороны, если предельные полезности, деленные на доли, vi0(xi)/δi , упорядочены одинаково вне зависимости от уровня общественного блага, то медианный потребитель не зависит от цены.
Сравним оптимальное количество общественного блага и его объем в равновесии при голосовании с долевым участием.
В особой ситуации, когда доли расходов равны предельным полезностям, соответствующим его оптимальному количеству, т. е. δi = vi0(ˆx), для всех участников выполнено соотношение: xˆi = xˆ, т. е. xˆ предпочитается всеми потребителями (а не только более чем их половиной) любой другой альтернативе.
Но при определении «правильных» долей финансирования мы должны опираться на приватную информацию о предпочтениях потребителей, т. е. решить проблему выявления предпочтений, трудности решения которой мы уже обсуждали и будем обсуждать ниже.
21Можно рассмотреть и несколько другую процедуру — голосование относительно величины издержек на производство общественного блага, r = c(x) (с индуцированными на множестве возможных общественных издержек предпочтениями v˜i(r) = vi(c−1(r))). Анализ этого механизма проводится по той же схеме. При этом оказывается, что величина c(¯xi ) представляет собой равновесное значение издержек. Таким образом, медианные общественные издержки соответствуют медианному уровню общественного блага, хотя эти две процедуры голосования подразумевают разные расходы (так как величина
px¯i = c0(¯xi )¯xi ,
вообще говоря, отлична от величины c(¯xi )).

11.6. Голосование простым большинством |
421 |
В общем случае мы можем ожидать как недопроизводства общественного блага (ˆxi , xˆ)), так и его перепроизводство.
Пусть, например, потребители финансируют общественное благо поровну, т. е. δi = m1 , где число потребителей m нечетное. Тогда в равновесии при голосовании объем потребления общественного блага xˆi будет таким, что
vi0 (ˆxi ) = m1 c0(ˆxi ).
С другой стороны, оптимальный (по Парето) объем потребления общественного блага есть величина xˆ, такая что
1 |
Xi I |
vi0(ˆx) = |
1 |
c0(ˆx). |
m |
m |
Таким образом, объем производства общественного блага в равновесии при голосовании с равными долями финансирования xˆi является оптимальным тогда и только тогда, когда средняя предельная полезность для этого количества равна предельной полезности медианного потребителя.
Легко придумать такой набор функций vi(x), что для любого объема потребления общественного блага x средняя предельная полезность больше предельной полезности медианного потребителя. В этом случае (при убывающей отдаче) можно доказать, что xˆ > xˆi . Если бы xˆ 6 xˆi , то
m1 c0(ˆx) = m1 X vi0(ˆx) > v˜i0 (ˆx) > v˜i0 (ˆxi ) = m1 c0(ˆxi ).
i I
Наоборот, если для любого объема потребления общественного блага x средняя предельная полезность меньше предельной полезности медианного потребителя, то xˆ < xˆi . Если бы xˆ > xˆi , то
m1 c0(ˆx) = m1 X vi0(ˆx) < v˜i0 (ˆx) 6 v˜i0 (ˆxi ) = m1 c0(ˆxi ).
i I
Пример 56 ((продолжение Примеров 54 и 55)):
В рассмотренном выше примере, когда
vi(xi) = 2αi ln xi и c(y) = y2,
имеем xˆi = √mαi и xˆ = √mα¯ , где α¯ = Pi I αi/m. Поэтому xˆ > xˆi тогда и только тогда, когда α¯ > αi .
Пусть, например, αi = i, и m нечетно. Тогда
α¯ = αi = i = m 2+ 1,
и объем производства общественного блага в равновесии при голосовании совпадает с оптимальным.
Если αi = i2 , то |
|
|
|
||
α¯ = |
(m + 1)(2m + 1) |
и αi = (i )2 = |
(m + 1)2 |
||
|
|
|
. |
||
|
4 |
||||
6 |
|
|
|
||
Поскольку α¯ > αi при m > 1, то xˆ > xˆi . |
|
|
|
||
Если αi = exp(γi), то при γ > 0 выполнено α¯ > αi |
и xˆ > xˆi . В то же время при γ < 0 |
выполнено α¯ < αi и xˆ < xˆi . |
4 |
