
- •Введение
- •Блага, множество допустимых альтернатив
- •Бинарные отношения и их свойства
- •Задачи
- •Неоклассические предпочтения
- •Задачи
- •Представление предпочтений функцией полезности
- •Задачи
- •Свойства предпочтений и функции полезности
- •Задачи
- •Рационализация наблюдаемого выбора
- •Задачи
- •Непротиворечивые, но неполные предпочтения
- •Полные, но противоречивые (нетранзитивные) предпочтения
- •Задачи
- •Поведение потребителя
- •Модель поведения потребителя: основные понятия и свойства
- •Бюджетное множество
- •Задача потребителя, маршаллианский спрос, непрямая функция полезности
- •Задача минимизации расходов и хиксианский спрос
- •Задачи
- •Дифференциальные свойства задачи потребителя
- •Задачи
- •Влияние изменения цен и дохода на поведение потребителя
- •Сравнительная статика: зависимость спроса от дохода и цен. Закон спроса
- •Оценка изменения благосостояния.
- •Задачи
- •Рационализация. Теорема Африата
- •Задачи
- •Восстановление квазилинейных предпочтений
- •Восстановление предпочтений на основе функции расходов
- •Проблема восстановимости предпочтений на всем множестве потребительских наборов
- •Интегрируемость (рационализуемость) спроса
- •Задачи
- •Задачи к главе
- •Поведение производителя
- •Технологическое множество и его свойства
- •Задачи
- •Задачи
- •Задачи
- •Затраты и издержки
- •Множество требуемых затрат
- •Функция издержек
- •Восстановление множества требуемых затрат
- •Задачи
- •Агрегирование в производстве
- •Задачи
- •Классическая модель экономики. Допустимые состояния
- •Общее равновесие (равновесие по Вальрасу)
- •Субъекты экономики в моделях общего равновесия
- •Модели общего равновесия
- •Некоторые свойства общего равновесия
- •Избыточный спрос
- •Задачи
- •Существование общего равновесия
- •Задачи
- •Парето-оптимальные состояния экономики и их характеристики
- •Характеризация границы Парето через задачу максимизации взвешенной суммы полезностей
- •Дифференциальная характеристика границы Парето
- •Задачи
- •Связь равновесия и Парето-оптимума. Теоремы благосостояния
- •Задачи
- •Существование равновесия в экономике обмена
- •Характеристика Парето-оптимальных состояний
- •Характеристика поведения потребителей
- •Потребительский излишек: определение, связь с прямой и обратной функциями спроса
- •Характеристика поведения производителей
- •Излишек производителя
- •Связь излишков с благосостоянием
- •Репрезентативный потребитель
- •Задачи к главе
- •Риск и неопределенность
- •Представление предпочтений линейной функцией полезности
- •Представление линейной функцией полезности: доказательство
- •Задачи
- •Предпочтения потребителя в условиях неопределенности
- •Задачи
- •Задача потребителя при риске
- •Задачи
- •Модель инвестора (выбор оптимального портфеля)
- •Задачи
- •Сравнительная статика решений в условиях неопределенности
- •Задачи
- •Задачи
- •Задачи к главе
- •Задачи
- •Равновесие Раднера в экономике с риском
- •Задачи
- •Задачи к главе
- •Налоги
- •Общее равновесие с налогами, не зависящими от деятельности
- •Общее равновесие с налогами на потребление
- •Задачи
- •Общее равновесие с налогами на покупку (продажу)
- •Задачи
- •Оптимум второго ранга. Налог Рамсея
- •Задачи
- •Задачи
- •Экстерналии
- •Модель экономики с экстерналиями
- •Проблема экстерналий
- •Задачи
- •Свойства экономики с экстерналиями
- •Задачи
- •Равновесие с квотами на экстерналии
- •Равновесие с налогами на экстерналии
- •Задачи
- •Рынки экстерналий
- •Задачи
- •Альтернативная модель экономики с экстерналиями
- •Задачи
- •Экстерналии в квазилинейной экономике
- •Задачи
- •Слияние и торг
- •Задачи
- •Торговля квотами на однородные экстерналии
- •Задачи
- •Задачи к главе
- •Общественные блага
- •Задачи
- •Квазилинейная экономика с общественными благами
- •Задачи
- •Равновесие с добровольным финансированием
- •Задачи
- •Равновесие (псевдоравновесие) Линдаля
- •Задачи
- •Долевое финансирование: общие соображения
- •Задачи
- •Голосование простым большинством
- •Равновесие с политическим механизмом
- •Задачи
- •Задачи
- •Задачи к главе
- •Примеры торга при асимметричной информации
- •Покров неведения и конституционный контракт
- •Задачи
- •Модели рынка с асимметричной информацией
- •Модификация классических моделей равновесия: равновесия с неотличимыми благами
- •Модель Акерлова: классическая постановка
- •Модель Акерлова как динамическая игра
- •Задачи
- •Монополия
- •Классическая модель монополии
- •Сравнительная статика
- •Анализ благосостояния в условиях монополии
- •Существование равновесия при монополии
- •Задачи
- •Ценовая дискриминация
- •Дискриминация первого типа. Идеальная дискриминация
- •Дискриминация второго типа (нелинейное ценообразование)
- •Задачи
- •Олигополия
- •Модель Курно
- •Свойства равновесия Курно в случае постоянных и одинаковых предельных издержек
- •Свойства равновесия Курно в случае функций издержек общего вида
- •Равновесие Курно и благосостояние
- •Модель Курно и количество фирм в отрасли
- •Задачи
- •Модель дуополии Штакельберга
- •Существование равновесия Штакельберга
- •Равновесие Штакельберга и равновесие Курно
- •Приложение
- •Задачи
- •Картель и сговор
- •Неоптимальность равновесия Курно с точки зрения олигополистов
- •Сговор
- •Картель
- •Задачи
- •Модель Бертрана
- •Продуктовая дифференциация и ценовая конкуренция
- •Модель Бертрана при возрастающих предельных издержках
- •Динамический вариант модели Бертрана (повторяющиеся взаимодействия)
- •Задачи
- •Модель олигополии с ценовым лидерством
- •Задачи
- •Модели найма
- •Модель с полной информацией
- •Задачи
- •Модель с ненаблюдаемыми действиями
- •Формулировка модели и общие свойства
- •Дискретный вариант модели со скрытыми действиями
- •Задачи
- •Модель найма со скрытой информацией
- •Модель найма со скрытой информацией при монопольном положении нанимателя: характеристики оптимальных пакетных контрактов
- •Модель найма с асимметричной информацией при монопольном положении нанимателя: общий случай
- •Задачи
- •Конкуренция среди нанимателей в условиях скрытой информации
- •Задачи
- •Модель сигнализирования на рынке труда (модель Спенса)
- •Введение
- •Статические игры с полной информацией
- •Нормальная форма игры
- •Концепция доминирования
- •Равновесие по Нэшу
- •Равновесие Нэша в смешанных стратегиях
- •Динамические игры с совершенной информацией
- •Динамические игры с несовершенной информацией
- •Статические игры с неполной информацией
- •Динамические байесовские игры
- •Игры и Парето-оптимальность
- •Сотрудничество в повторяющихся играх
- •Игры торга
- •Вогнутые и квазивогнутые функции
- •Однородные функции
- •Теорема Юнга
- •Теоремы о неподвижной точке
- •Теоремы отделимости
- •Теорема об огибающей
- •Свойства решений параметрической задачи оптимизации
- •Теоремы о дифференцируемости значения экстремальной задачи
3.3. Влияние изменения цен и дохода на поведение потребителя |
99 |
dp| ∂R∂x xdp, соответствующей эффекту дохода. В частности, если благо нормальное в том смысле, что > 0, то эффект дохода будет положительным, и, как следствие, будет выполнен (локально) закон спроса.
Для приведенного разложения на эффект дохода и эффект замены можно предложить аналог в случае, когда изменения цен не являются бесконечно малыми. Пусть, как и выше, x0 — оптимальное решение задачи потребителя при ценах p0 и доходе R = p0x0 , и цены становятся равными p1 . Тогда разложение на эффект дохода и эффект замены при компенсирующем изменении дохода по Слуцкому будет иметь следующий вид:
x = x1 − x0 = [x1 − x(p1, p1x0)] + [x(p1, p1x0) − x0].
Первое слагаемое соответствует эффекту дохода (изменению дохода с R = p0x0 до p1x0 ), а второе слагаемое — эффекту замены. Аналогично, с использованием компенсирующего изменения дохода по Хиксу получим следующее разложение:
x = [x1 − x(p1, e(p1, x0))] + [x(p1, e(p1, x0)) − x0].
Заметим, что еще два подобных разложения можно получить, поменяв в приведенных формулах местами p0 и p1 (и, соответственно, x0 и x1 ). Таким образом, имеем четыре различных естественных разложения на эффект дохода и эффект замены. Очевидно, что в пределе, при малых приращениях, эти четыре разложения становятся идентичными.
3.3.2Оценка изменения благосостояния.
В этом разделе мы приведем оценки изменения благосостояния потребителя при изменении ситуации, в которой он осуществляет выбор, т.е. изменении цен p и доходов R.
Перед экономистами часто стоит задача оценить изменения в благосостоянии потребителей при проведении мероприятий экономической политики. Рассмотрим две ситуации (до проведения мероприятий экономической политики и после). В первой их них потребитель сталкивается с ценами p0 и доходом R0 , во второй — с ценами p1 и доходом R1 . Поскольку рассматривается только выбор на классических бюджетных множествах, то здесь можно использовать введенное ранее понятие непрямой функции полезности v(p, R). В то время как обычная функция полезности u(x) соответствует оценке потребителем потребительских наборов x, непрямая функция полезности соответствует оценке потребителем самих ситуаций выбора. Если v(p0, R0) < v(p1, R1), то вторая ситуация более благоприятна для потребителя, а если v(p0, R0) > v(p1, R1), то менее благоприятна.
Вообще говоря, мы можем говорить лишь о направлении изменения благосостояния, а не оценивать его величину. И, тем не менее, при расчетах издержек и выгод мероприятий экономической политики пытаются получить количественные оценки таких изменений. При этом используются так называемая непрямая денежная функция полезности.
Определение 34:
Непрямая денежная функция полезности µ(q; p, R) — это доход, который требуется, чтобы при ценах q потребитель мог бы иметь тот же уровень полезности, что и при ценах p, располагая доходом R, т. е. µ(q; p, R) = e(q, x(p, R)).
Другими словами, денежная непрямая полезность µ(q; p, R) определяется как непрямая функция полезности для функции расходов e(q, x), рассматриваемой как функция полезности. Опишем, как ее можно использовать и какие проблемы при этом возникают.
Непрямая денежная функция полезности определяется на основе некоторого (произвольного) «эталонного» вектора цен q > 0. Оценка изменения благосостояния при этом будет равна
µ(q) = µ(q, p1, R1) − µ(q, p0, R0) = e(q, x(p1, R1)) − e(q, x(p0, R0)) = e(q, x1) − e(q, x0),
3.3. Влияние изменения цен и дохода на поведение потребителя |
100 |
где x0 — спрос потребителя в исходном состоянии, а x1 — спрос потребителя в новом состоянии. Значение µ(q), вообще говоря, может быть различным для разных векторов q и поэтому, соответствующие оценки изменения благосостояния содержат элемент субъективизма. Исключением являются квазилинейные предпочтения (предпочтения, которые можно описать квазилинейной функцией полезности).
В случае квазилинейности предпочтений все меры благосостояния эквивалентны с точностью до постоянного множителя, а в случае, когда цена последнего блага равна единице (единица «квазилинейного» блага является единицей измерения, numeraire), они совпадают. Покажем это, вычислив µ(q) для квазилинейной функции полезности u(x1, . . . , xl) = s(x1, . . . , xl−1) + xl в предположении, что pl = 1. Вспомним, что в этом случае непрямая функция полезности имеет вид
l−1
X
v(p−l, 1, R) = s(x1(p−l), . . . , xl−1(p−l)) + R − pixi(p−l).
i=1
Пользуясь соотношениями двойственности, получаем, что функция расходов в случае квазилинейных предпочтений??, как мы видели выше, имеет вид e(p, x) = u(x) − s(x−l(p−l)) + p−lx−l(p−l). По определению непрямой денежной функции полезности µ(q, p, R) = e(q, x(p, R)), поэтому
µ(q, p, R) = v(p, R) − s(x−l(q−l)) + q−lx−l(q−l).
Как видим, при любом фиксированном векторе цен q непрямая денежная функция полезности совпадает с точностью до константы (зависящей от q) с той непрямой функцией полезности, которая определяется естественной для квазилинейных предпочтений нормировкой. Отсюда по определению µ(q) имеем
µ(q) = µ(q, p1, R1) − µ(q, p0, R0) = v(p1, R1) − v(p0, R0).
В общем случае, когда значение µ(q) зависит от выбора q, естественными кандидатами на роль вектора цен q представляются p0 и p1 (соответственно, цены в исходной ситуации, до изменений, и цены после изменений). В первом случае получим меру изменения благосостояния, называемую эквивалентным изменением дохода (EV ), а во втором — меру изменения благосостояния, называемую компенсирующим изменением дохода (CV ).
Определение 35:
Эквивалентное изменение дохода (эквивалентная вариация) — это такое приращение исходного дохода, которое обеспечивает в исходного ценах тот же уровень благосостояния, что и после изменений:
x(p0, R0 + EV (p0, R0, p1, R1)) x(p1, R1).
Несложно убедиться, что
EV (p0, R0, p1, R1) = e(p0, x1) − R0 = µ(p0).
Действительно, доход, достаточный для того, чтобы при ценах p0 обеспечить данному потребителю такой же уровень полезности, как и в ситуации после изменений (т. е. при ценах p1 и доходе R1 ), по определению непрямой денежной функции полезности равен µ(p0, p1, R1) = e(p0, x1). Поэтому требуемое изменение дохода по сравнению с исходным доходом R0 равно
e(p0, x1) − R0 = e(p0, x1) − e(p0, x0) = µ(p0, p1, R1) − µ(p0, p0, R0) = µ(p0),
где мы воспользовались тем, что если x0 — спрос потребителя при ценах p0 , то e(p0, x0) = R0 .

3.3. Влияние изменения цен и дохода на поведение потребителя |
|
|
|
101 |
|||||||||
Пример 22: |
|
|
|
|
|
|
|
|
|
|
|
||
Пусть функция спроса и функция расходов потребителя равны |
|
|
|
|
|
|
|
||||||
x(p, R) = p1p2 + a2(p1)2 ; |
(p2)2 + a2p1p2 ! |
и e(p, x) = |
p2 |
+ a2p1 |
|||||||||
|
Rp2 |
|
a2Rp1 |
|
|
p1p2 |
(√ |
x1 |
+ a√ |
x2 |
)2 |
|
|
соответственно. Найдем эквивалентную вариацию, отвечающую изменению цен от p0 = (2, 1) до p1 = (1, 2) при условии, что доход оставался неизменным и был равен R. Непрямая денежная функция полезности для данного потребителя будет иметь вид
µ(q, p, R) = q1q2(p2 + a2p1)R. p2p1(q2 + a2q1)
Таким образом,
p0p0(p1 + a2p1)
EV (p0, R, p1, R) = µ(p0, p1, R) − R = 1 2 2 1 R − R.
p12p11(p02 + a2p01)
Подставляя |
p0 |
= (2, 1) |
и |
p1 |
= (1, 2) |
, получаем |
EV = |
1−a22 R |
. |
4 |
|
|
|
|
|
|
1+2a |
|
|||||
Определение 36:
Компенсирующее изменение дохода (компенсирующая вариация) — это такое уменьшение дохода в новой ситуации, которое позволяет в новых ценах достигнуть уровень полезности
исходной ситуации:
x(p0, R0) x(p1, R1 − CV (p0, R0, p1, R1)).
По определению денежной непрямой функции полезности доход, достаточный для того, чтобы при ценах p1 обеспечить данному потребителю такой же уровень полезности, как и в ситуации до изменений (т. е. при ценах p0 и доходе R0 ), равен µ(p1, p0, R0) = e(p1, x0). Кроме того, µ(p1, p1, R1) = e(p1, x1) = R1 . Поэтому компенсирующая вариация равна изменению денежной непрямой функции полезности при q = p1 :
CV (p0, R0, p1, R1) = e(p1, x0) − R1 = µ(p1),
Отметим, что введенное понятие компенсирующей вариации — это то же самое изменение дохода, с которым мы сталкивались при рассмотрении закона спроса (см. ???).
Пример 23 (продолжение Примера 22):
В рассматриваемом случае при постоянном доходе компенсирующая вариация равна |
|
||||||||||||||||
|
|
|
|
|
0 |
1 |
0 |
1 |
p1p1 |
(p0 |
+ a2p0) |
|
|||||
|
|
|
|
|
1 |
2 |
2 |
1 |
|
|
|
||||||
|
|
|
CV (p |
, R, p |
, R) = R − µ(p |
, p |
, R) = R − |
|
|
R. |
|
||||||
|
|
|
p20p10(p21 + a2p11) |
|
|||||||||||||
При p |
1 |
= (1, 2) |
и p |
0 |
= (2, 1) компенсирующая вариация равна |
CV = |
(1−a2) |
|
|||||||||
|
|
(2+a2) |
R. |
4 |
|||||||||||||
Рассмотрим соотношение между этими мерами изменения благосостояния в простом случае, когда изменяется только цена одного блага (случай, который интересует нас при анализе последствий налогообложения): R0 = R1 = R, p01 > p11 , p0−1 = p1−1 = p−1 . Очевидно, что потребитель при таком изменении не может ухудшить своего положения, поскольку множество доступных ему потребительских наборов расширяется: v(p0, R) 6 v(p1, R). Введем следующие упрощенные обозначения:
EV = EV (p0, R0, p1, R1), CV = CV (p0, R0, p1, R1), x0 = x(p0, R), x1 = x(p1, R).
3.3. Влияние изменения цен и дохода на поведение потребителя |
|
|
|
|
102 |
||||
µ(p0 |
,p1 |
x2 |
|
x2 |
|
|
|
|
|
,R) |
|
|
|
|
|
|
|
||
|
|
EV |
|
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
CV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
x1 |
µ(p1,p0,R) |
x1 |
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
x1 |
|
|
|
|
|
R/p0 |
R/p1 |
R/p0 |
R/p1 |
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
|
|
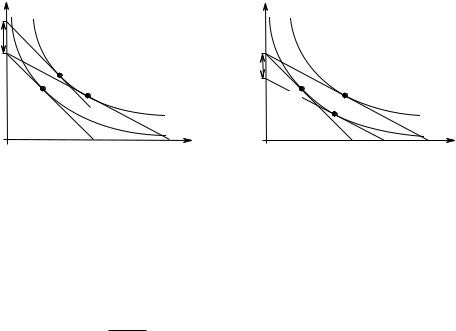
Рис. 3.8. Эквивалентная и компенсирующая вариация при R0 = R1 = R, p0 |
> p1 |
, p0 |
= p1 |
= 1 |
|||||
|
|
|
|
|
1 |
1 |
2 |
2 |
|
Кроме того, поскольку в данном случае меняется только цена первого блага, с целью упрощения записи не будем в дальнейшем указывать остальные цены p−1 и доход R в качестве аргументов функций.
Рис. 3.8 предлагает графическую иллюстрацию для эквивалентной и компенсирующей вариаций в случае двух благ, когда цена второго блага равна единице (p02 = p12 = 1).
Проинтегрировав тождество ∂e(p,x) = h1(p, x) (лемма Шепарда для теории потребления)
∂p1
по цене первого блага от p11 до p01 , получим
Z p0
p11
1 h1(t, x)dt = e(p01, x) − e(p11, x).
Эквивалентную и компенсирующую вариации можно представить в аналогичном виде (как уменьшение значения функции расходов для одной и той же кривой безразличия при падении цены первого блага с p01 до p11 , см. Рис. 3.8):
EV = e(p01, x1) − R = e(p01, x1) − e(p11, x1),
CV = R − e(p11, x0) = e(p01, x0) − e(p11, x0).
Таким образом,
p0 |
|
p0 |
Zp11 |
|
Zp11 |
1 |
h1(t, x1)dt, CV = |
1 |
EV = |
h1(t, x0)dt. |
Как известно?? из курсов микроэкономики начального и промежуточного уровня, изменение потребительского излишка вычисляется по формуле
|
p0 |
|
Zp11 |
CS = CS(p0, p1) = |
1 |
x1(t)dt. |
Из того, что p01 > p11 следует, что в данном случае все три величины неотрицательны (они положительны, если спрос строго положителен):
EV > 0, CV > 0, CS > 0.
Если эффект дохода неотрицателен (рассматриваемое благо — нормальное), то
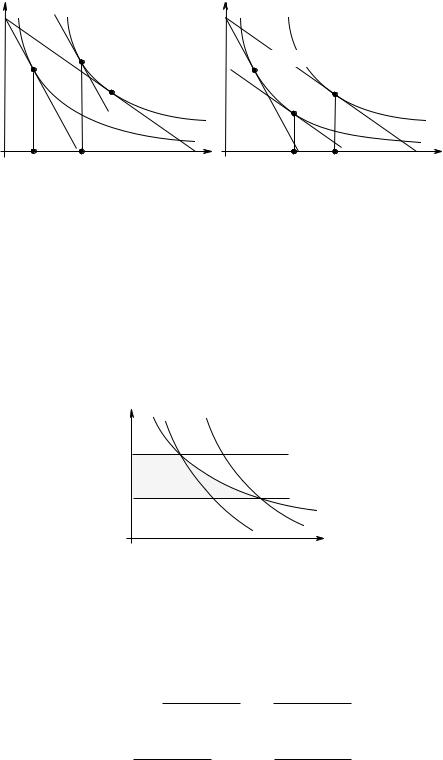
h1(t, x0) 6 x1(t) 6 h1(t, x1) при p11 6 t 6 p01.
Докажем эти неравенства формально. Спрос потребителя на первое благо, если его цена равна t (где p11 6 t 6 p01 ) и доходе R равен x1(t) = x1(t, R). Пусть теперь доход потребителя стал равен e(t, x0). Несложно заметить, что доход потребителя уменьшился на
3.3. Влияние изменения цен и дохода на поведение потребителя |
103 |
неотрицательную величину CV (p01, t) = R − e(t, x0). В силу нормальности блага имеем, что x1(t, e(t, x0)) 6 x1(t, R). Из соотношений взаимности имеем, что x1(t, e(t, x0)) = h1(t, x0). Таким образом, мы доказали левое из требуемых неравенств.
Аналогичным образом доказывается правое неравенство. Предположим, что доход потребителя изменился с R до e(t, x1), т. е. увеличился на неотрицательную величину EV (t, p11) = e(t, x1) − R. При этом x1(t, R) 6 x1(t, e(t, x1)) = h1(t, x1).
x2 |
|
x2 |
|
|
h(t,x1) |
h(p0 |
,x0)=x0 |
x(t) |
|
1 |
|
h(p11,x1)=x1 |
|
x(t) |
|
|
|
|
h(t,x0) |
|
x1 |
|
x1 |
x1(t) |
h1(t,x1) |
h1(t,x0) x1(t) |
|
Рис. 3.9. Соотношения между хисксианским и маршаллианским спросом, используемые при доказательстве взаимосвязи эквивалентного, компенсирующего изменений дохода и потребительского излишка
Эти неравенства (в случае двух благ) иллюстрирует Рис. 3.9.
Интегрируя доказанные неравенства по t от p11 до p01 , получаем, что имеет место соотношение
CV 6 CS 6 EV.
Рис. 3.10 иллюстрирует это соотношение. Здесь CV = S(ABEF ), CS = S(ABDF ) (заштрихованная область), EV = S(ACDF ).
p1 |
|
|
h1(p1,x1) |
|
p0 |
A |
B |
C |
|
1 |
|
|
|
|
p11 |
|
|
D |
x1(p1) |
F |
|
E |
||
|
|
|
||
|
|
h1(p1,x0) |
x1 |
|
Рис. 3.10. Связь между потребительским излишком, эквивалентной и компенсирующей вариациями
Пример 24 (продолжение Примеров 22 и 23):
Положим p12 = 1 до p02 = 1 в формулах для эквивалентной и компенсирующей вариации:
p1(1 + a2p0)
CV = R − 1 1 R =
p01(1 + a2p11)
p0(1 + a2p1)
EV = 1 1 R − R =
p11(1 + a2p01)
p0 − p1
1 1 R, p01(1 + a2p11)
p0 − p1
1 1 R. p11(1 + a2p01)
3.3. Влияние изменения цен и дохода на поведение потребителя |
104 |
Найдем также изменение потребительского излишка. Для этого требуется проинтегрировать
спрос на первое благо, равный x1(p1) = |
R |
|
|
. Как несложно проверить, |
|||||||||||||
p1(1+a2p1) |
|||||||||||||||||
|
|
ln |
|
t |
! |
0 |
1 |
|
|
|
|
|
|
||||
|
|
|
|
= |
|
|
|
. |
|
|
|||||||
|
|
1 + a2t |
|
t(1 + a2t) |
|
|
|||||||||||
С учетом этого |
|
|
|
|
|
|
|
|
|
1 + a2p0 ! |
− R ln |
1 + a2p1 ! |
|||||
CS = R |
p1 |
x1(t, 1, R)dt = R ln |
|
|
|||||||||||||
Z |
p0 |
|
|
|
0 |
|
|
|
|
1 |
|
||||||
1 |
1 |
|
|
|
|
|
|
|
|
p1 |
|
|
p1 |
||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
||||||
или |
|
CS = R ln p11 |
(1 + a2p10)! . |
|
|
||||||||||||
|
|
|
|
|
|
p10 |
(1 + a2p11) |
|
|
|
|
|
|||||
Можно заметить, что изменение потребительского излишка можно представить через эквивалентную и компенсирующую вариации следующим образом:
|
! |
|
! |
|
CS = R ln 1 + |
EV |
= −R ln 1 − |
CV |
|
R |
R |
. |
||
При малых t верно приближение ln(1 + t) ≈ t, поэтому при малых изменениях цены все три измерителя изменения благосостояния примерно равны. Кроме того, ln(1 + t) < t при t 6= 0,
поэтому, в подтверждение теории, выполнены неравенства CV < CS < EV . |
4 |
В случае квазилинейных предпочтений (при достаточно большом доходе) отсутствует эффект дохода для товара, который входит нелинейно. В этом случае записанные выше неравенства, связывающие маршаллианский и хиксианский спрос, выполняются как равенства и,
следовательно,
EV (p0, p1) = CS(p0, p1) = CV (p0, p1).
Геометрически эта ситуация означает что все три кривые спроса, изображенные на диаграмме, совпадают; следовательно, совпадают и три рассмотренные меры благосостояния.
Вообще говоря, полезности разных потребителей не сравнимы друг с другом, и их бессмысленно складывать. Однако на основе денежных мер изменения благосостояния можно получать некоторые оценки мероприятий экономической политики.
Предположим, что существуют n потребителей с функциями полезности ui(xi) и доходами Ri . Пусть цены изменились с p0 до p1 . Пусть, кроме того, в результате этого изменения цен суммарная величина компенсирующей вариации положительна, т. е.
|
|
|
|
|
Xi |
CVi(p0, Ri, p1, Ri) > 0. |
|
|
|
Покажем, что существует такое перераспределение доходов {Ri0}: |
i Ri0 6 i Ri ), что vi(p1, Ri0) > |
||||||||
v (p0 |
, R |
) |
i |
, то есть, возможно компенсировать изменение цен |
каждому потребителю. |
||||
i |
i |
|
|
P |
P |
||||
По определению компенсирующей вариации имеем, что |
|
|
|||||||
|
|
|
|
CVΣ = Xi |
CVi(p0, Ri, p1, Ri) = Xi |
(Ri − ei(p1, xi(p0, Ri))) > 0 |
|||
Мы можем выбрать Ri0 так, что Ri0 > ei(p1, xi(p0, Ri)) (достаточно взять Ri0 = ei(p1, xi(p0, Ri)) + CVΣ/n). Покажем, что в этом случае vi(p1, Ri0) > vi(p0, Ri) i.
Воспользовавшись возрастанием непрямой функции полезности по доходу и свойством двойственности между vi(·, ·) и ei(·, ·), получим
vi(p1, Ri0) > vi(p1, ei(p1, xi(p0, Ri))) = vi(p0, Ri).
